动力设备弹簧板-橡胶隔振系统设计与动态特性
黄雪涛,顾 亮
(1.山东交通学院汽车工程学院,山东济南 250357;2.北京理工大学机械与车辆学院,北京 100081)

动力设备弹簧板-橡胶隔振系统设计与动态特性
黄雪涛1,顾亮2
(1.山东交通学院汽车工程学院,山东济南250357;2.北京理工大学机械与车辆学院,北京100081)
摘要:针对某动力设备工作过程中产生的振动冲击现象,构建该动力设备振动系统的数学模型,计算其工作过程中对地面产生的冲击激励。设计新型弹簧板-橡胶层叠式隔振系统;利用橡胶材料的非线性、橡胶块与弹簧板之间的接触耦合关系,构建弹簧板-橡胶层叠式隔振系统的非线性有限元仿真模型。仿真结果表明:在载荷的作用下,隔振系统的最大变形量为12.73 mm,最大应力为280.80 MPa,地面基础的振幅由原来的2.380 mm衰减到0.386 mm,衰减了83.78%。该研究成果为层叠式隔振系统的设计研发提供了理论基础和技术支撑。
关键词:弹簧板-橡胶;隔振技术;动力设备;动态特性
动力设备隔振系统不但能够降低动力装置自身的振动,而且能够有效隔断动力装置的冲击激励向地面基础的传播,对于提高动力设备的工作精度和改善工作环境有着重要意义。动力装置隔振系统的性能主要取决于动力设备工作过程中产生的冲击激励、隔振系统各部件的性能及部件之间的耦合关系。
文献[1-2]建立隔振系统的动力学模型,采用理论分析的方法研究单刚体隔振件的隔振效果;文献[3]利用弹簧的大变形非线性及阻尼液的阻尼特性,建立弹簧-阻尼液隔振系统的数学模型;文献[4]构建隔振系统的数学模型,研究隔振系统的主动控制技术;文献[5]建立多自由度隔振系统的数学模型,研究阻尼特性对隔振效果的影响;文献[6]建立蜗轮发电机隔振系统的有限元模型,分析系统参数对隔振效果的影响;文献[7]研究微振动隔振技术,建立微振动隔振系统的数学模型;文献[8]研究粘弹性隔振器的动力学特性,提出描述粘弹性材料动力学性能的六参数模型;文献[9-10]探讨橡胶隔振系统叠加模型的参数识别方法,并对橡胶隔振器的动态特性进行分析;文献[11]得出隔振系统最优阻尼下共振频率的物理意义;文献[12]研究新型组合式颗粒阻尼器减振的性能;文献[13]研究隔振系统耦联参数的多目标优化设计;文献[14-15]研究柔性基础上金属橡胶隔振系统的混沌响应;文献[16]研究圆筒式阻尼垫的设计。上述对于隔振系统的研究大多采用的是理论分析方法,且主要集中在弹簧-阻尼液和橡胶隔振系统的研究上。而弹簧板-橡胶层叠式隔振系统的研究涉及到弹簧板和橡胶块的大变形非线性、橡胶材料的非线性及弹簧板-橡胶块之间的耦合接触关系,成为现阶段隔振领域研究的热点和难点。
本文以动力设备的弹簧板-橡胶隔振系统为研究对象,采用有限元数值模拟、理论建模和数值分析相结合的方法,构建动力设备振动系统的数学模型,分析动力设备工作过程中产生的冲击激励,并利用橡胶块材料的非线性、大变形非线性及弹簧板-橡胶块之间的耦合接触关系,完成弹簧板-橡胶层叠式隔振系统的设计研发,利用构建的层叠式隔振系统的非线性有限元模型,计算隔振系统的变形和应力分布,探讨隔振系统的动态特性及对动力设备冲击激励的衰减效果。
1振动系统的数学模型

图1 曲柄滑块机构简图
动力设备工作过程中产生的冲击激励主要来自曲柄滑块机构的动不平衡力,故动力设备振动系统的数学模型可以通过曲柄滑块的动力学方程来构建。动力设备曲柄滑块机构见图1。
滑块运动过程中产生的动不平衡力
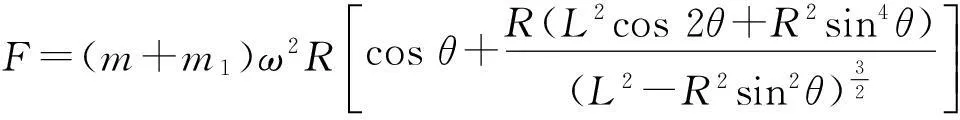
式中:m为滑块质量;m1为动力设备上模具质量;ω为曲柄角速度;R为曲柄半径;θ为曲柄转角;L为连杆长度。
动力设备在工作过程中产生的动不平衡力可以转化为工作时间t的正弦函数。动力设备振动系统的数学模型为:
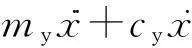
式中:my、ky、cy分别为动力设备的质量、整体刚度与阻尼系数;x为动力设备对地面的冲击位移激励;F0为正弦激励的幅值。
动力设备对地面的振动冲击位移激励为:

(1)
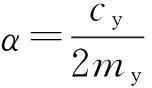
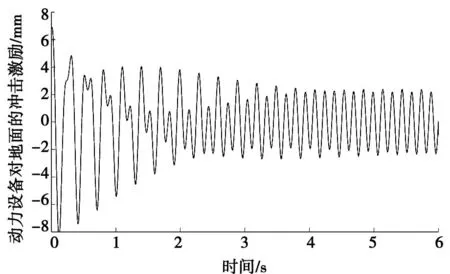
图2 动力设备对地面的冲击激励随时间的变化曲线
根据某动力设备的具体结构参数,由式(1)可以得出未安装隔振系统即动力设备直接安装在地面基础上时,动力设备对地面的冲击激励随时间的变化曲线如图2所示。由式(1)知,未安装隔振系统时,动力设备对地面的位移冲击激励由两部分叠加而成:一部分冲击激励来自动力设备的初始位移和初速度引起的阻尼自由振动,该部分位移激励在阻尼力的作用下逐渐衰减为0;另一部分冲击激励来自动力设备动不平衡力引起的阻尼强迫振动,该冲击激励收敛于幅值为2.38 mm的正弦曲线(见图2)。根据文献[17],动力设备基础允许的振动幅值为1 mm,故该动力设备必须安装隔振系统。
2隔振系统设计与强度分析
由于动力设备的工作频率较低,在工作过程中产生的动态载荷较大,采用传统的弹簧-阻尼液隔振系统虽能起到隔振效果,但由于该隔振系统自身的强度、刚度及可靠性不足,弹簧易产生永久变形甚至断裂,使用一段时间后其隔振效果明显下降,故不能满足该动力设备的隔振需求;而纯橡胶式隔振系统的可靠性虽然能满足动力设备的使用要求,但因其固有频率较高,只能对动力设备的高频冲击激励起到隔振作用,故也不能满足该动力设备的隔振需求。根据动力设备的动载计算结果,结合有限元仿真技术和隔振理论,采用弹簧板-橡胶层叠式结构的隔振系统。该隔振系统利用橡胶块的几何非线性、橡胶的材料非线性以及阻尼特性和弹簧板-橡胶之间的接触耦合特性实现衰减动力设备冲击激励的效果。该弹簧板-橡胶系统共有22层隔振单体,每个隔振单体包括1块弹簧板和6块高强度特制橡胶,橡胶块与弹簧板之间采用粘结的方法组合成一体,最上层和最下层的钢板仅起承载作用。
弹簧板-橡胶隔振系统放置在动力设备的4个边角位置,通过弹簧板和橡胶块的弹性和阻尼作用来隔离动力设备对地面的振动冲击。由于动力设备对地面冲击动载荷较大,隔振系统的工作条件恶劣,为防止隔振系统在工作过程中出现断裂、疲劳破坏等故障,必须对隔振系统进行结构强度分析。弹簧板-橡胶隔振系统有限元模型采用超弹性材料来模拟橡胶的材料非线性,其特性参数通过单轴拉伸、双轴拉伸和平面剪切试验获取,基于橡胶厂家提供的试验数据做出的橡胶材料的特性曲线如图3所示。
弹簧板和橡胶之间的耦合接触关系通过创建粘结接触面进行模拟,有限元模型的前处理在通用软件HYPERMESH中进行,模型的求解在非线性求解器ABAQUS中完成。约束弹簧板-橡胶隔振系统与地面接触处的节点自由度,取动力设备自重与其工作过程中产生的最大动载荷之和作为作用在隔振系统上的载荷,并用作用在隔振系统上表面的集中力来表示。其中,弹簧板和橡胶均采用10 mm的空间四面体单元划分,该弹簧板-橡胶隔振系统共有28 303个节点、46 461个单元,有限元模型如图4所示。
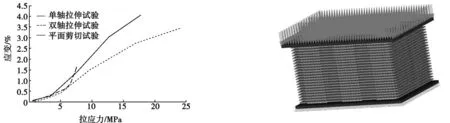
图3 橡胶材料试验曲线 图4 弹簧板-橡胶隔振系统有限元模型
采用有限元软件对弹簧板-橡胶隔振系统在工作过程中的强度和变形情况进行仿真分析,得到隔振系统的变形情况如图5所示。
由图5可知:在动力设备载荷的作用下,隔振系统的最大变形量为12.73 mm,主要位于弹簧板-橡胶隔振系统的最上层。在外部载荷作用下,弹簧板和橡胶之间接触耦合,弹簧板内嵌于刚度较小的橡胶之中,弹簧板-橡胶隔振系统从与动力设备接触的顶层开始发生压缩变形,产生与外部载荷方向相反的力。随着变形量的增加,产生的弹力逐渐增大,直到弹簧板和橡胶块的变形力与动力设备的载荷大小相等时,弹簧板-橡胶隔振系统达到新的平衡。
弹簧板-橡胶隔振系统的应力分布情况如图6所示。
由图5可知:在外部载荷作用下,弹簧板-橡胶隔振系统的应力较大,最大应力为280.80 MPa,主要集中在钢板弹簧与橡胶块接触的下表面;承载钢板的应力也较大,最大应力为75.49 MPa,主要集中在上面板与橡胶块接触的部位;橡胶部分的应力较小,最大应力为3.43 MPa,主要集中在橡胶块与钢板接触耦合的部位。弹簧板-橡胶层叠式隔振系统各个部位的应力都远小于对应材料的许用应力,故该弹簧板-橡胶隔振系统的强度满足要求。

图5 隔振系统变形图 图6 隔振系统应力图
3隔振系统的动态特性
动力设备对地面基础的载荷主要包括两部分,即设备自身重力引起的静载荷和设备工作过程中由曲柄连杆机构产生的冲击动载荷。由于动力设备工作过程中产生的动载荷为随时间变化的正弦函数,故动力设备工作过程中对弹簧板-橡胶隔振系统产生的冲击激励也是随时间变化的动态载荷,其大小为动力设备自重产生的静载荷与工作过程中产生的动态冲击激励之和。在动力设备4个边角位置安装4个弹簧板-橡胶隔振系统,为了研究问题的方便,假设4个弹簧板-橡胶隔振系统受到的冲击载荷相等,均为动力设备总载荷的1/4。
为了研究弹簧板-橡胶层叠式隔振系统的隔振性能及其在动力设备载荷作用下的动态响应, 需对该系统做频率响应分析和瞬态动力学分析。 在对弹簧板-橡胶隔振系统进行频率响应分析时, 在隔振系统的顶层施加一个z向的单位位移虚约束,计算隔振系统在0~200 Hz范围内的频率响应函数,得到的隔振系统底层承压板即地面基础的频率响应曲线如图7所示。由图7可知,在弹簧板-橡胶层叠式隔振系统顶层承压板虚位移约束的激励下,隔振系统底层承压板即地面基础产生了动态响应。由于弹簧板和橡胶块之间的耦合作用及橡胶材料的阻尼作用,地面基础的动态响应较顶层的冲击激励有明显的衰减,且地面基础动态响应的振幅在0~200 Hz随着频率的提高而逐渐变大,其振动幅值的变化范围为0.158~0.166,对顶层位移激励的衰减率为83.47%~84.16%;在0~200 Hz地面基础的振动相位随着频率的增加而降低,其相位值由0 Hz的176.57°变为200 Hz时的176.42°,相位接近180°,这主要是由于隔振系统顶层位移激励与z轴的正方向相反,而产生的地面基础动态响应的方向与z轴的正方向相反所致。
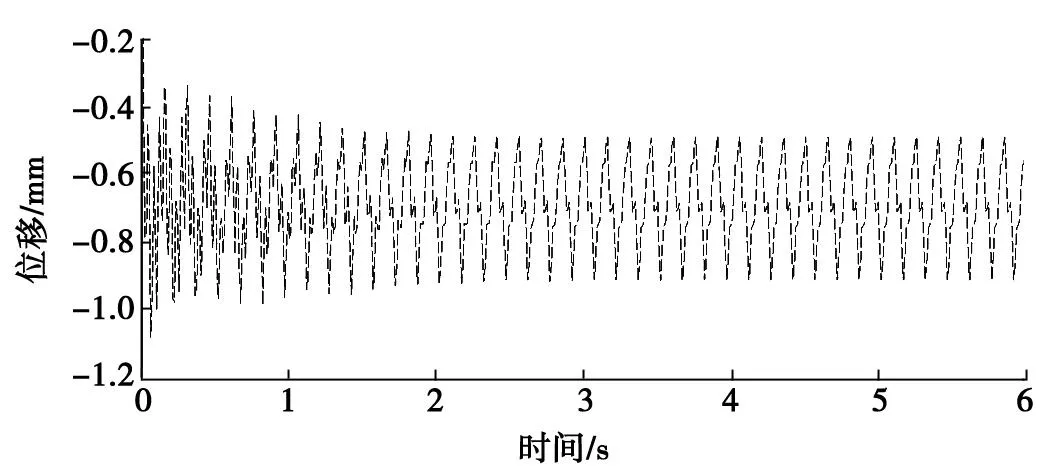
图8 安装隔振系统后地面基础的位移变化曲线
在对弹簧板-橡胶层叠式隔振系统进行瞬态动力学分析时,在有限元仿真分析软件中构建时间相关的动载荷和动态分析的时间步长,设定橡胶的阻尼系数和弹簧板-橡胶系统的结构阻尼,并把定义的随时间按正弦规律变化的动态载荷施加到弹簧板-橡胶隔振系统的顶层承压板上,得到安装弹簧板-橡胶隔振系统后地面基础的振动情况如图8所示。由图8可知,在动力设备动载冲击激励的作用下,弹簧板-橡胶层叠式隔振系统产生了动态响应。在最初的1 s内,由于初位移和隔振系统初变形的影响,隔振系统的振动幅值较大;随着振动时间增加,隔振系统在动力设备动载冲击和系统结构阻尼及橡胶阻尼的作用下,逐渐达到平衡状态。达到平衡状态后,与地面基础直接接触的最后一层承压板的振动幅值即安装弹簧板-橡胶隔振系统后地面基础的振动幅值为0.386 mm,而未安装隔振系统时地面基础的振动幅值为2.380 mm,振动衰减了83.78%。安装弹簧板-橡胶隔振系统后,动力设备地面基础的振动幅值符合动力设备设计规范对地面振动幅值的要求,改善了工人的工作条件及附近居民的生活环境。
4结论
1)构建动力设备振动的数学模型,得出动力设备振动冲击激励的变化规律。
2)设计层叠式弹簧板-橡胶隔振系统,建立弹簧板-橡胶隔振系统的非线性有限元模型。仿真结果表明:在动力载荷的作用下,隔振系统的最大变形量为12.73 mm,最大应力为280.80 MPa,小于对应材料的允许应力,隔振系统的强度满足要求。
3)隔振系统的动态特性分析表明:安装隔振系统后,地面基础的振动幅值由原来的2.380 m衰减到0.386 m,振动衰减了83.78%。
参考文献:
[1]LI W L,LAVRICH P.Prediction of power flows through machine vibration isolators[J].Journal of Sound and Vibration,1999,224(4):757-774.
[2]LI W L,DANIELS M,ZHOU W.Vibrational power transmission from a machine to its supporting cylindrical shell[J].Journal of Sound and Vibration,2002,257(2):283-299.
[3]CARMEN HO,LANGN Ziqiang,STEPHEN A Billings.Design of vibration isolators by exploiting the beneficial effects of stiffness and damping nonlinearities[J].Journal of Sound and Vibration,2014,333:2489-2504.
[4]LI H, HU S D,LI H Y,et al. Active vibration suppression of payloads with a conical Isolator[J].Journal of Intelligent Material Systems and Structures,2014,25(7):871-880.
[5]LIU Lei,TAN Kok Kiong,GUO Yu,et al.Active vibration isolation based on model reference adaptive Control[J].International Journal of Systems Science,2014,45(2):97-108.
[6]CHAD Van der Woude,SRIRAM Narasimhan.A study on vibration isolation for wind turbine structures[J].Engineering Structures,2014,60:223-234.
[7]KAMESH D,PANDIYAN R,GHOSAL A. Modeling,design and analysis of low frequency platform for attenuating micro-vibration in space-craft[J].Journal of Sound and Vibration,2010,329(17):3431-3450.
[8]王跃,刘志敏,李世其,等.约束阻尼型隔振器粘弹材料振动温升研究[J].振动工程学报,2010,23(5):585-590.
[9]潘孝勇.橡胶隔振器动态特性计算与建模方法研究[D].杭州:浙江工业大学,2009.
[10]PAN Xiaoyong,CHAI Guozhong.Modeling of rubber isolators and application in dynamic analysis for a SDOF System[J].International Journal of Vehicle Design,2009,49(4):259-274.
[11]王超新,孙靖雅,张志谊.最优阻尼三参数隔振器设计和试验[J].机械工程学报,2015,51(15):90-96.
[12]杜妍辰,张虹.组合式颗粒阻尼器的减振实验研究[J].中国机械工程,2015,26(14):1953-1958.
[13]黄伟,徐建,朱大勇,等.主动隔振下固支薄板基础振动抑制的参数多目标优化[J].计算力学学报,2015,32(4): 457-464.
[14]李玉龙,白鸿柏,何忠波,等.金属橡胶非线性隔振系统混沌特性[J].中国机械工程,2015,26(14):1871-1876.
[15]李玉龙,白鸿柏,何忠波.柔性基础上金属橡胶隔振系统混沌响应研究[J].振动与冲击,2015,34(14):100-105.
[16]张春晓,何翔,李磊,等.高黏弹沥青阻尼垫研制及其冲击隔离性能试验研究[J].振动与冲击,2015,34(14):194-199.
[17]中华人民共和国机械工业部.GB50040—96动力设备设计规范[S].北京:中国计划出版社,1996.
(责任编辑:杨秀红)
Design and Dynamic Characteristic of Vibration Isolation System of
Dynamic Equipment Spring Steel-Rubber
HUANGXuetao1,GULiang2
(1.SchoolofAutomotiveEngineering,ShandongJiaotongUniversity,Jinan250023,China;
2.SchoolofMechanicalEngineering,BeijingInstituteofTechnology,Beijing100081,China)
Abstract:For the vibration impacts appeared during operation of dynamic equipment, a mathematical model of vibration system of the equipment is built to calculate the impact stimulus on the ground. Combined with the
characteristics of vibration isolation system, a new cascading vibration isolation system is designed.The characteristics of nonlinear characteristic of rubber and contact coupling relationship between rubber and spring steel is used to build the nonlinear finite model of spring steel-rubber vibration isolation system. The results of simulation show that, in loaded conditions, the maximum deformation of the vibration isolation system is 12.73 mm, and the maximum stress is 280.8 MPa. And the vibration amplitude of ground base is reduced from 2.380 mm to 0.386 mm, reduced by 83.78%. The achievement provides a theoretical basis and a technical support for cascading isolation design.
Key words:spring steel-rubber; vibration isolation technology; dynamic equipment; dynamic characteristic
文章编号:1672-0032(2015)04-0003-05
中图分类号:TH113;U461
文献标志码:A
DOI:10.3969/j.issn.1672-0032.2015.04.002
作者简介:黄雪涛(1978—),男,山东东明人,讲师,工学博士,主要研究方向为振动与噪声控制.
收稿日期:2015-09-20

