直升机地面滑跑飞行力学研究

许勤勇，殷士辉，徐玉貌

(中航工业直升机所，江西 景德镇 333001)



直升机地面滑跑飞行力学研究

许勤勇，殷士辉，徐玉貌

(中航工业直升机所，江西 景德镇 333001)

在直升机地面滑跑模型中引入了精确的飞行力学模型，形成了直升机地面滑跑飞行力学模型。以Peters/He广义动态入流理论建立入流模型，采用等环面积法划分桨叶微段，以叶素理论建立旋翼气动模型。以刚体动力学方法建立直升机地面滑跑模型。使用试飞数据对模型进行验证，吻合较好。文中对直升机地面滑跑进行计算分析，得到了操纵、姿态等的变化规律，为飞行员地面滑跑操纵提供了建议。

直升机地面滑跑；飞行力学；操纵

0 引言

作为一种方便快捷的飞行器，直升机在民用和军事领域都得到了广泛的应用，在国民生活和国防建设中扮演着越来越重要的角色。这就对直升机的性能和安全提出了更高的要求。直升机地面滑跑的性能和安全是直升机性能和安全的重要组成部分。与空中状态相比，直升机在地面滑跑时，作用在直升机上的力除了空气动力、重力和惯性力之外，还有起落架机轮与地面之间的摩擦力和反作用力。地面运动过程中，直升机的速度比较低，直升机机身及气动面的气动力影响较小。同时，直升机地面滑跑时会受到地面效应[1]的影响，面临复杂的气动环境。

良好的地面滑跑性能是一架直升机圆满完成任务的基本保障，同时直升机地面滑跑的安全也非常重要。国内外有一些对直升机地面滑跑进行仿真的方法。A.M.Volodko[2]研究了前三点式起落架直升机地面运动。在文中，他以刚体动力学方法建立了直升机地面运动的微分方程，旋翼和尾桨的推力和机身阻力通过考虑地面效应的常用空气动力学分析来确定。考虑了机轮受到的滚动摩擦力、滑动摩擦力、转向阻力及其随速度的变化；分析了发生倾倒的原理，给出了影响因素和改善的操纵方法。但其对空气动力处理得比较粗糙，没有给出具体的空气动力学模型，不能对整个滑跑过程进行模拟。杨永文[3]等也进行了直升机地面运动的研究，但文中同样没有提到具体的空气动力学模型。

本文通过建立精度较高的直升机地面滑跑飞行力学模型，对直升机地面滑跑的飞行力学特性进行分析。文中对直升机地面滑跑的加速和稳定滑跑等过程进行模拟，分析滑跑过程中力和姿态的变化，为飞行员地面滑跑的操纵提供指导。

1 直升机地面滑跑飞行力学建模

1.1 飞行力学模型

使用Peters/He广义动态入流理论建立入流模型，其诱导速度的任意谐波次数、任意阶次径向型函数组成的级数形式为：

这样，旋翼桨叶的每一个计算微段气动中心的诱导速度可写作：

计算旋翼/机身气动干扰时，由动量理论的假设，在理想状态下旋翼远场处，有：

vfar=2v0i

其中，vfar为远场处的垂向诱导速度，v0i为旋翼桨尖轨迹平面处的等效诱导速度。在平尾、尾桨和垂尾的位置处，旋翼尾流产生的垂向诱导速度：

viz=kizvidx

旋翼模型以叶素理论为基础, 用等环形面积划分旋翼微段。

当地气动迎角为：

叶素的升力和阻力的表达式为：

因为风轴系和当地叶素坐标系之间刚好相差气动迎角α，因此，得到当前叶素在叶素坐标系中的气动力分量：

FZ=Lift×cos(α)-Drag×sin(α)

FT=Lift×sin(α)+Drag×cos(α)

再沿桨叶半径积分，就能得到瞬态的气动载荷和气动力矩。将各片桨叶上的力转化到桨毂中心处，得到桨毂中心处的力和力矩。地面效应则使用经验公式对旋翼推力进行修正。

尾桨拉力为：

TTR=CTTRρkblπΩTR2RTR4

机身的空气动力通过风洞试验得到，平垂尾采用叶素理论进行计算。

直升机飞行力学方程为：

ϑ

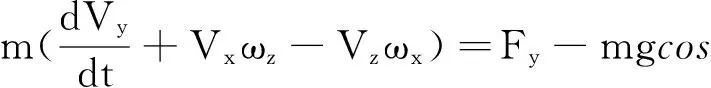
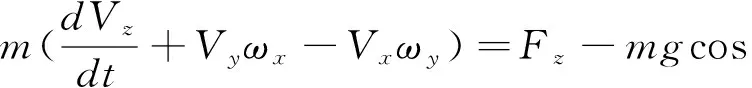
使用定步长Newton-Raphson 法对飞行力学方程进行线化求解，线化形式的系统方程：

1.2 地面滑跑建模

直升机滑跑在以重心为原点的体轴系里进行分析。地面限制了直升机在垂直、俯仰、滚转方向的自由度，惯性系统的运动微分方程如下：

Mza=Me-TtrLtr+Mzj

质量流量计远程智能诊断系统实现了对该公司现场86台质量流量计远程集中监控管理，应用大数据实时智能诊断运算分析给出了量化结果。

Za=Tsinγ-Ttr+zf

其中：m，G，Jz-直升机质量，重力以及偏航转动惯量；Vx，Vy-速度分量；T，S-旋翼拉力、纵向力、侧向力；Ttr，Ltr-尾桨推力和直升机重心到尾桨的距离；Xf，Zf，Mz-空气动力以及作用于机身的偏航力矩；Fu，Zu-反作用于起落架的切向力和侧向力；Fl,Fr-分别作用于左右主起落架的切向力；b，c-起落架轮距以及起落架轴线到直升机重心的距离；ε，θ0-旋翼轴预设角和直升机地面静态迎角；γ-直升机滚转角。

本文建立的模型为后三点式起落架模型。起落架受力和形变为：

其中：a=c+d-轮距；Δe-主起落架变形差异；xm-纵向重心位置；ym，hm分别为直升机重心到旋翼旋转平面和地面的距离。

当Pl<0，左起落架离开地面，直升机绕右起落架-尾轮轴向右侧翻。地面反作用于第i个起落架的切向和横向力取决于相应的垂直反作用力Pi和摩擦系数fj:

Fi=fxPi，Zi=fyPi

同时，对控制转向的尾轮还有如下条件：Zn=0。

直升机非定常地面运动中摩擦力的表达式如下：

fx=ff+fx|β|

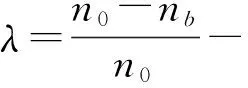
在直升机飞行动力学模型的基础上，加入地面滑跑模型，形成完整的直升机地面滑跑飞行力学模型。完整的直升机地面运动飞行力学方程如下：

ϑ-Fu

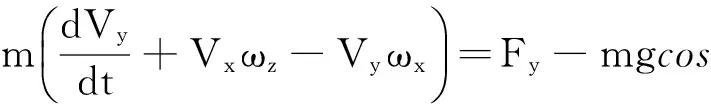
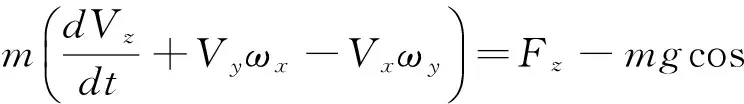
2 模型验证和分析

2.1 模型验证

本文以UH-60A直升机[5]为例进行计算，重量为7600kg，重心为正常重心，验证采用的试飞数据为“黑鹰”直升机地面直线加速滑跑试飞数据。将计算结果与飞行试验数据进行对比验证，如图1-图3。

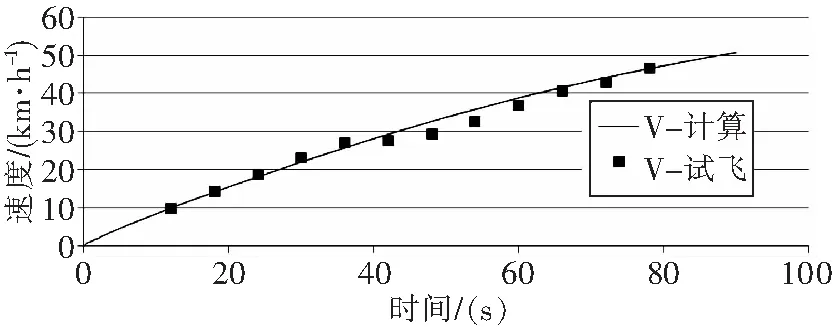
图1 速度对比

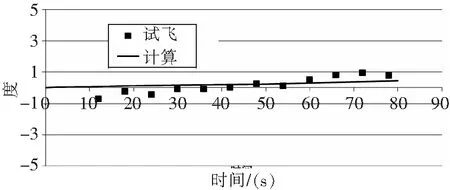
图2 滚转角对比

图3 俯仰角对比

可以看出，本文建立的直升机地面运动飞行力学模型的计算结果和试飞数据吻合得比较好，验证了直升机地面运动飞行力学模型的精度。

2.2 直升机地面滑跑分析

地面滑跑是直升机地面运动中最常用的一种运动方式。滑跑过程中直升机起落架轮胎与地面保持接触，并有力的作用，运动速度较慢。直升机地面滑跑时，飞行员通过操纵总距和纵向周期变距控制速度，操纵横向周期变距调节滚转角，操纵尾桨距保持航向。这时的滚转角是由于起落架左右轮受力不同，起落架产生的形变不同而引起的。

固定模型总距为30%，纵向周期变距分别取10%，20%，30%，40%(中立位置为0，前极限为100%)，横向保持中立。直升机的速度、滚转角、轮胎支持力的变化如图4-图9。

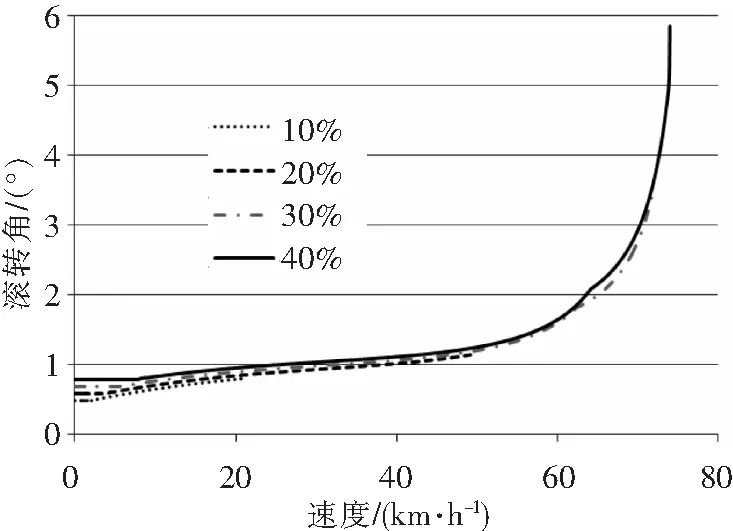
图5 地面滑跑的滚转角随速度变化

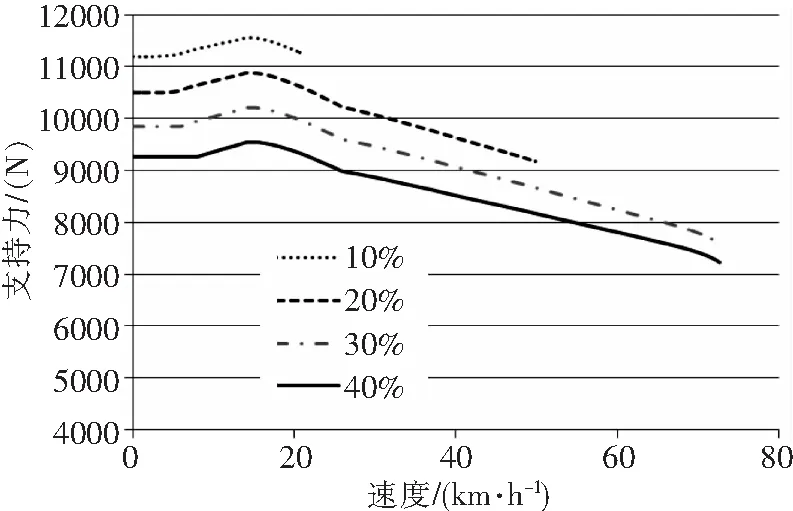
图6 地面滑跑尾轮支持力随速度变化

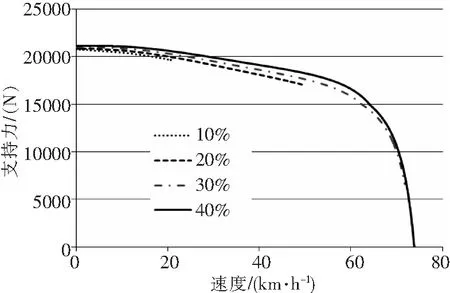
图7 地面滑跑左轮支持力随速度变化

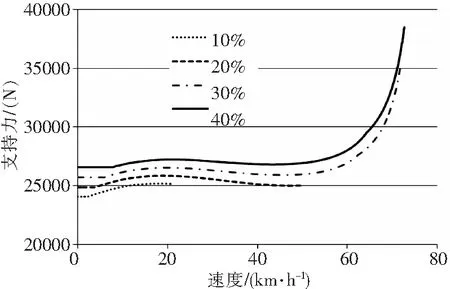
图8 地面滑跑右轮支持力随速度变化

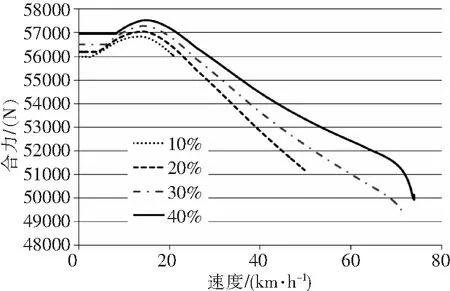
图9 起落架支持力合力随速度变化

在总距足够时，随着直升机纵向周期变距的增加，稳定滑跑的速度随之增加；滑跑速度越快，直升机的滚转力矩越大，这会引起直升机起落架左右轮胎受力不同而使滚转角增大；当速度增加到一定数值时，左轮支持力变为0而离地，这时直升机就可能发生侧翻。

滚转角的变化见图5。速度相同时，纵向操纵变化引起的滚转角变化很小；操纵相同时，速度增加，滚转角也随之增加。操纵相同时，速度增加，左轮支持力减小，右轮支持力增加；右起落架形变比左起落架大，由此产生了滚转角。滚转角过大会导致直升机侧翻，因此，直升机做地面滑跑时应注意滚转角的大小，控制滑跑速度或者通过横向操纵减小滚转角都可以预防侧翻的发生。

图9为直升机起落架支持力合力的变化。合力有一个先增加后减小的过程，这说明直升机旋翼拉力随速度先减小后增加。这是由于直升机滑跑速度增加会引起地面效应的减小和旋翼诱导速度的增加；速度较小时地面效应的减小为主要影响因素，故旋翼拉力减小；速度较大时地面效应影响变得很小，旋翼拉力随速度的增加而增大。

由于地面运动的特殊性，直升机以某一速度进行地面滑跑，可以通过多种总距和纵向操纵组合来实现。为进一步分析操纵量与直升机滑跑速度的关系，使操纵量与直升机滑跑速度的关系更清楚明了，给飞行员进行地面滑跑提供操纵量的参考，本文通过计算给出了不同速度的几种可行的操纵量组合，见图10。

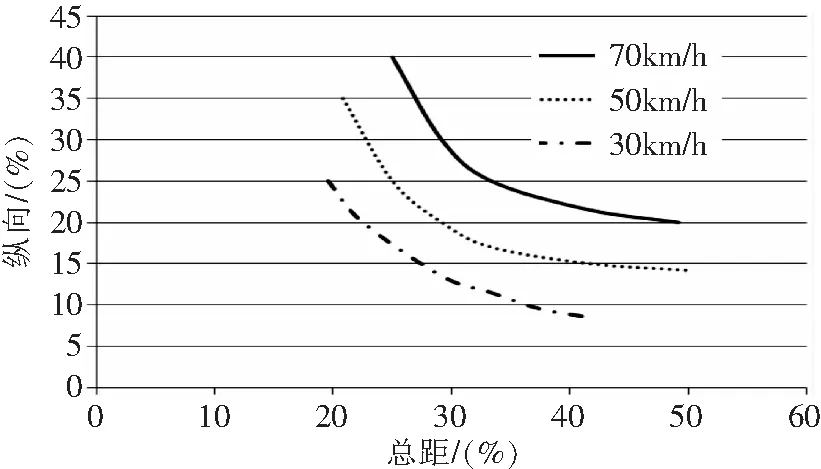
图10 速度与总距、纵向操纵量的关系

飞行员可根据需要的滑跑速度在图中选取合适的总距、纵向操纵量，作为实际操纵的参考。对应的横向、尾桨距见表1。(横向操纵中立位置为0，向右为正，范围为-100%到100%。)

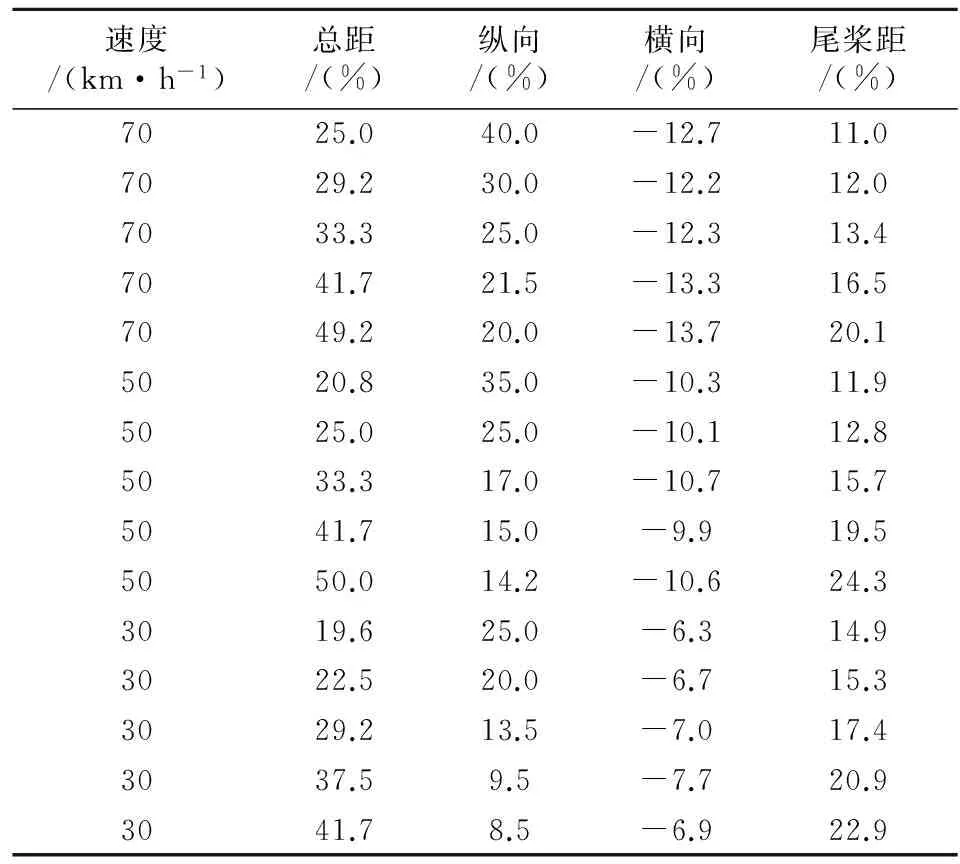
表1 不同速度的操纵量

横向操纵过大会导致直升机侧翻。为提供横向操纵的限制，本文对最严酷的条件(极限重量、重心、高度)和20节侧风下滑跑做了分析，最后得到不发生侧翻的横向操纵范围为-44%到20%。实际操纵应小于极限值。

3 总 结

直升机地面运动由于受地面的影响和限制而具有了不同的特性。本文针对直升机地面滑跑的操纵和姿态等进行研究，在直升机地面运动中引入了飞行力学分析，建立了可信的直升机地面运动飞行力学模型。通过计算分析了直升机地面滑跑的速度、姿态和起落架受力变化，给出了不同滑跑速度的操纵建议，为飞行员提供参考，为设计具有更好地面运动特性的直升机提供依据。

[1] 王适存.直升机空气动力学[M].南京：南京航空航天大学出版社,1990.

[2] Volodko A M. Dynamic of Helicopter Ground Motion[C].Russia:24TH European Rotocraft Forum Marseilles，1998．

[3] 杨永文，孟庆松，吕长生，直升机地面运动动力学研究[C].第二十四届全国直升机年会，2008.

[4] Bakker E，Pacejka H B．A New Tire Model with An Application in Vehicle Dynamics Studies[R]．SAE Paper，1989.

[5] UH-60A black hawk engineering simulation program : Volume I - Mathematical model[Z]. USAAVSCOM, Howlett, 1989.

Flight Dynamics Analysis of Helicopter Taxiing

XU Qinyong, YIN Shihui, XU Yumao

(China Helicopter Research and Development Institute, Jingdezhen 333001, China)

In this paper, the helicopter taxiing model was established with more accurate helicopter flight dynamics model, formed the helicopter flight dynamics model of taxiing. The rotor inflow model utilized Peters-He generalized dynamic inflow model, and the rotor aerodynamic model was based on the blade element theory, adopted equal annulus area as criteria for dividing blade. Use the rigid-body dynamics method to set up the helicopter taxiing model. Using flight test data to verify this model, we obtained the higher credibility. We analyzed the taxiing, got the change rule of the manipulation and attitude, and provided pilots suggestions.

helicopter taxiing; flight dynamics; manipulation

2015-04-10

许勤勇(1989-)，男，湖南娄底人，硕士，助理工程师，主要研究方向：直升机飞行力学。

1673-1220(2015)02-006-05

V212.13+1

A