基于PSDNN神经网络的稳风速控制系统的分析与应用
辛 颖,易 晖
(中国直升机设计研究所,江西 景德镇 333001)
基于PSDNN神经网络的稳风速控制系统的分析与应用
辛 颖,易 晖
(中国直升机设计研究所,江西 景德镇 333001)
介绍采用多点静压落差法测量风洞试验段的风速,并对其特点进行说明;针对低速直流式风洞稳风速控制困难,易受外部环境影响的问题,提出了一种多层前向神经元网络PSDNN。PSDNN神经网络的风洞稳风速控制系统不仅保留了原来的控制系统,同时还提高了稳风速控制的精度,为得到更好的试验数据提供保障。
PSDNN神经网络;稳风速控制系统;多点静压落差法
0 引言
风洞流场品质是反映风洞试验段内气流流动特性的关键因素,直接影响试验数据的精准度。对于低速风洞,其流场品质关键指标包括风速、方向场、气流温度、湍流度、动压稳定性等。低速风洞的稳风速控制系统是整个风洞重要的系统之一。稳风速控制系统具有大滞后、非线性、参数时变等特点,并且随风速、开闭口模式、模型姿态角、环境等因素的变化,及运行时间的不同,风洞本身的参数都会发生变化。这是一种非常复杂的控制系统,其传递函数很难用精确的数学模型表达。对于直流开口式低速风洞,极易受外界环境的影响,控制艰难。在复杂系统的辨识和自适应控制中,神经网络得到广泛的应用,出现许多基于两层神经网络的PID控制方法[1]。这种方法多数是前馈神经网络,适合静态网络,产生的控制信号为误差的比例、积分和微分的线性组合。大量实践证明,这种组合会引起快速性和超调量之间的矛盾[2]。为了克服这些缺点,本文提出了一种动态多层前向神经元网络PSDNN,其动态特性不仅通过网络的链接方式和反馈方式实现,而且还包含其内部的PSD神经元来实现反馈。
1 多点静压落差法测量试验段风速的原理
在低速风洞试验时,需要测量来流的速度或动压,如果通过在模型前安装风速管来测量,则会产生风速管对模型的气动力干扰,从而影响风速测量及模型试验数据的准确度。因此,通常采用压强落差法来测量试验段的风速,对于直流开口式低速风洞,可采用多点静压落差法[3]。
多点静压落差法采用两组静压探头测量反馈风速,一组放置在收缩段入口处平直部分内壁,探头与壁面平齐,垂直于气流方向;另外一组放置在收缩段出口处平直部分内壁,探头的安装和方向与前一组相同。将两组静压探头分别用管路连通做物理平均,输入到微压差传感器的相应输入端口,则微压差传感器的输出端口给出静压差值,反馈给PLC和上位计算机,如图1所示。多点静压落差法选取截面上的多点静压做平均,减小了由于外界环境及模型大攻角状态引起的风速不均匀性对风速反馈值的影响。

图1 多点静压落差法示意图
在风洞收缩段入口和出口分别取B截面和A截面,在试验段中心取C点。由于气流在流动过程中存在能量损失,下游的气流总压比上游的总压要低。利用伯努利方程及连续方程:
其中,Pi是i(A、B)截面静压值;vj是j(A、B、C)截面风速;ρ是空气密度;k是压强损失系数;Sm是m(A、B、C)截面的面积。
可得:

由式(3)可知,在风洞吹风试验时,通过测得AB截面的静压落差和大气密度,即可以得到试验段中心的风速。
2 系统工作原理及神经网络算法
系统运行时,由工控机发出设定信号给变频器,驱动电机和风扇旋转,在风洞形成气流。在风洞入口处设置落差测压点PA和PB,由微压差传感器测量截面A、B之间的压差,不同压差对应不同试验段风速。压差信号由数采板采集,经过神经网络运算,待试验段达到设定风速并满足控制精度后,停止给定信号,此时采集数据。如果风速精度达不到要求,则持续给出调节信号,直到满足风速精度。
神经网络PSDNN是一种多层前向神经元网络[4],与一般多层前向神经元网络形式相似,不同之处在于隐含层。一般多层前向神经元网络中的神经元的输入输出特性是相同和静态的,而PSDNN隐含层的神经元是由比例元、求和元和微分元组成,输入输出函数分别为比例、求和、微分函数,既有静态又有动态。PSDNN的动态特性不仅是通过网络的链接方式或反馈方式来实现,而且还包含PSD神经元来实现反馈,也就是说用神经网络加快PSDNN神经元的参数来调节风速。

图2 稳速压控制系统原理图
PSD神经元是2×3×1结构,包括输入层的2个神经元(u1,u2),隐含层的3个神经元(uP,uS,uD)和输出层的1个神经元(uy)。输入层接受外部信息,其中u1为对象的期望输出,u2为对象的实际输出。输入层神经元经过连接权重,进入隐含层。隐含层再经过连接权值,进入一个比例神经元的输出层,它完成整个网络控制规律的综合和输出,见图3。
输入层(u1,u2)可表示为采样时刻的函数(u1,u2)=[r(k),y(k)]。
隐含层(up,us,uD)表示为:

图3 PSDNN控制结构

在神经网络学习中,使实际输出和理想输出偏差绝对值最小,则权值wij正比于rij,规则为:
其中,m,d>0 ,是学习速率,z(k)是教师信号。根据随机逼近理论,当m很小时,权值收敛于定值。
输出层(uy)表示为:
uy(k)=w1(k)uP(k)+w2(k)us(k)+
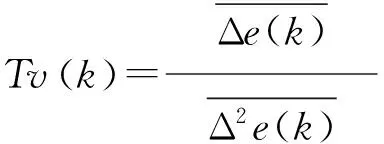
用神经网络作为控制系统的控制器时,权重初值的选取严重影响神经网络的学习和收敛速度。因为权重初值决定了学习起点和收敛初始方向。神经网络PSDNN按其独特的原则选取连接权重初值,这个原则是按照单神经元自适应PSD控制算法来确定的。选取输入层至隐含层的连接权重初值w1j=1,w2j=-1,隐含层至输出层的连接权重分别为wj=1,r0(k),r1(k),则自适应PSD控制为:
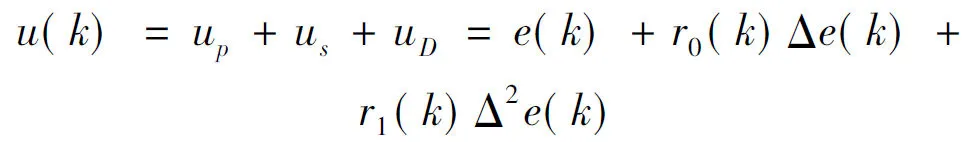
(9)

(10)
其中,r0(k),r1(k)可自动调整[5]。
这为PSDNN的连接权重值指出了可行方案,单神经元自适应PSD算法已经得到广泛使用,利用单神经元自适应PSD算法参数选取经验,加快PSDNN的调整速率,这不一定是最优选择,但一定是可行选择。
稳定性是控制系统最重要的性能之一,PSDNN控制算法也必须符合稳定性要求,否则将失去使用价值。稳定性分析需要从目标函数出发,本系统的目标函数为:E(k)=0.5(r(k)-y(k))2=0.5e2(k),权重值wi(k+1)=wi(k)-ηi∂E(k)/∂wi(k)。根据李雅普诺夫定理,ΔE(k)<0,系统是稳定的,于是可以得到0<η<2(PPT)-1,其中:
可见,只要学习速率满足上式的条件,就可以保证整个系统的全局稳定性,上式不但指出了系统的收敛条件,也指明了学习步长的取值范围,因此可以在保证系统收敛性的条件下,适当变化学习步长,以达到较好的学习效果和较快的收敛速度。
针对时变非线性系统[4]的被控对象:
取教师信号e(k),m=0,学习速率为0.7,0.8,0.9。将基于PSDNN神经网络算法、新型PID-NNC神经网络控制系统[6]及新型PIDNN神经网络控制系统[7]的仿真曲线进行对比,PSDNN的稳风速控制程序具有更稳定、精度更高、响应更快及超调小的特点(图4,图5)。

图4 PID-NNC控制系统仿真曲线(上)及新型PIDNN控制系统仿真曲线(下)
3 结 论
目前已经存在LabWindows调试成功的带死区PSDNN稳风速控制程序,获得了令人满意的效果,并在风洞中得到实际的应用。并且从仿真曲线和应用中看,PSDNN稳风速控制程序的自适应性更强,为在工业领域发展提供了良好的基础。随着神经网络理论研究的不断深入和控制理论的不断发展,这种控制方法应该具有更加广泛的工业应用前景。

图5 PSDNN控制系统仿真曲线
[1] 朱春波,包 钢,程树康,等. 基于比例阀的气动伺服系统神经网络控制方法的研究[J].中国机械工程,2001,12(12):1412-1414.
[2] Sun F C, Sun Z Q. Stable neural network-based adaptive control for sampled-data nonlinear systems[J]. IEEE Trans on Neural Networks, 1998,9(5):956-968.
[3] 易 晖,熊建军,汤永等. 多点静压落差法在风洞稳速压控制系统中的分析与应用[J].直升机技术,2013(4) :60-62.
[4] 吕鹏涛,惠增宏. NF-3风洞神经网络自适应稳风速控制系统研制[J].实验流体力学,2009,23(4):82-86.
[5] 崔皆凡,刘 艳,李 玥,等. 基于PSD算法的神经元PID多电机同步控制[J].机床与液压,2013, 41(19):18-21.
[6] 牛玉刚,赵建从,杨成梧. 一种新型神经网络控制器的研究[J].系统工程与电子技术,2000,22(6):45-83.
[7] 吴志敏. 基于新型PID神经网络的自适应控制系统研究[J].科学技术与工程,2008,1(8):76-79.
Analysis and Application of Wind Velocity Control System Based on PSDNN Neural Network
XIN Ying, YI Hui
(China Helicopter Research and Development Institute, Jingdezhen 333001, China)
This paper introduced multi-point static pressure method to measure wind velocity of wind tunnel, and described the characters. Due to the difficulties of wind speed control for low speed lineal wind tunnel low and influence of external environment, a multilayer previous neural network PSDNN was presented. The system was not only remain conventional control system, but also had higher precision, then this method ensured getting better test data.
PSDNN neural network; wind velocity control system; multi-point static pressure method
2015-09-15
辛 颖(1987-),女,辽宁省辽阳市人,硕士,工程师,主要研究方向:风洞试验技术。
1673-1220(2015)04-016-04
V211.74
A
———重庆建成世界一流汽车风洞

