悬索锚固区下料长度精细算法
魏远栋 杨林恺
(1.江西省交通设计研究院有限责任公司 南昌 330002; 2.江西省公路科研设计院 南昌 330002)
悬索锚固区下料长度精细算法
魏远栋1杨林恺2
(1.江西省交通设计研究院有限责任公司南昌330002;2.江西省公路科研设计院南昌330002)
摘要悬索桥主缆的下料是影响结构成桥状态的重要参数。文中基于中心索股的长度计算结果,提出了悬索锚固区各索股下料长度的精细算法。采用有限元软件建模,以悬链线索单元模拟主缆,根据结构的成桥状态计算出中心索股主缆的无应力长度;考虑锚固端索股的空间位置构造差异性,采用自编程序对各索股下料长度进行相对于中心索股长度的修正。以一座主跨110 m悬索桥为工程依托,对该精细算法进行验证,并给出了悬索锚固区各索股的精确下料长度。
关键词自锚式悬索桥索股下料长度精细化计算
悬索桥主缆的下料是影响结构成桥状态的重要参数。目前,研究悬索桥的理论方法较多。文献[1]根据已有的悬索桥分析理论[2],通过迭代算法得到成桥状态结构的线形和内力。文献[3]基于分段悬链线理论研究了自锚式悬索桥线形精确计算方法。但是,考虑到实际主缆为大体积构件,索股的空间位置分布位置差异性,特别是锚固区段主缆一般采用分层分散的方式锚固,每根索股经过散索套后到达锚固断面的锚固位置不同,相应锚固区各索股下料长度也不一致,因此有必要针对该部位的主缆下料长度作精细化计算。本文以一座悬索桥为依托,采用自编程序得出基于中心索股的无应力长度求解主缆下料长度的精细化计算方法。
1计算假定
计算方法考虑以下基本假定。
(1) 主缆为理想柔性材料,既不受压也不受弯。
(2) 主缆横截面积在外荷载作用下变化微小,忽略不计。
(3) 主缆材料满足胡克定律,应力与应变呈线性关系。
2精确计算中心索股无应力长度
悬索的主缆以悬链线索单元模拟[4],对主缆单元进行离散,除索鞍过渡段,其他位置主缆均离散为分段悬链线,累计各段悬链线单元的长度,加之索鞍处主缆圆弧段长度,即可得到中心索股主缆的准确下料长度。
3悬索锚固区各索股下料长度的精细算法
悬索锚固区是指散索鞍至锚垫板区段,如图1中所示A-A断面至B-B断面,其中A-A断面为散索断面,B-B断面为缆索的锚固断面;该区段缆索悬链线段可简化为直线段。修正计算按图2所示建立局部空间坐标系,设散索断面中心点A点坐标(x1,0,z1),锚端中心点坐标B点坐标为(x2,0,z2),根据设计资料可知A,B2点坐标,进而可求得缆索锚固区中心索股的有应力长度L及中心索股与水平向夹角θ;在图示局部坐标系中将A,B点的绝对坐标转换为相对坐标,即A(0,0,0),B(-Lcosθ,-Lsinθ)。

图1 锚固端立面图
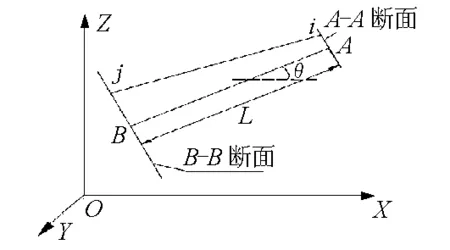
图2 锚固端简化坐标系
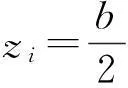
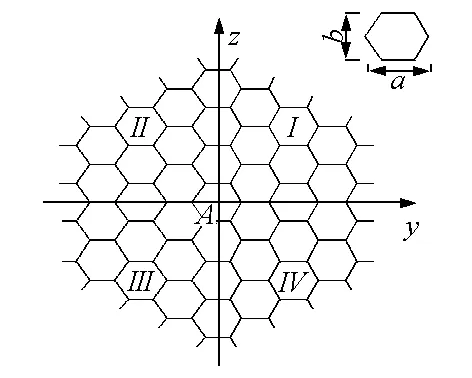
图3A-A断面局部坐标系

图4B-B断面局部坐标系
将任一索股的局部坐标点i点及j点坐标换算至整体坐标系,得到整体坐标系中任一索股两端的坐标点分别为
i点坐标:(-zisinθ,-yi,zicosθ)
j点坐标:(-zjsinθ,-Lcosθ,-yj,
zjcosθ-Lsinθ )
则i,j点坐标即代表I象限(其他象限计算方法相同)任意索股单元两端的坐标点,经计算,有应力长度为

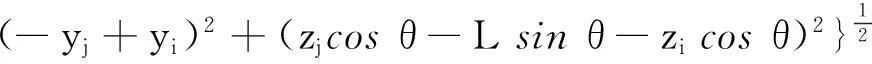
式中:S为缆索锚固区主缆的弹性伸长量ΔS及其无应力长度u之和,根据材料力学的基本公式,有关系式:(F/EA+1)u=S;F为缆索锚固区主缆的内力;E为缆索的弹性模量;A为缆索断面的横截面积。因此,建立缆索锚区主缆的局部坐标系,经过空间坐标变换,将任一索股的局部坐标统一至整体坐标系下,即可确定任一索股两端的相对位置坐标,精确求出缆索锚固区主缆各索股的下料长度。
4自锚式悬索桥工程算例
4.1 算例描述
本文的依托工程为一座跨径布置为40 m+110 m+40 m的自锚式悬索桥,以此对本文提出的精细算法进行验证。图5为成桥计算模型,拉索采用悬链线索单元模拟,塔顶主索鞍以单圆曲线过渡,图6为主缆索中各索股的横断面布置及索股编号;主要计算参数见表1。

图5自锚式悬索桥有限元计算模型


图6 主缆断面布置及索股编号
4.2 验证结果
按上述方法计算得到主缆中心索股无应力长度为240.584 m,缆索锚固区无应力索长9.947 m,通过对缆索锚固区精细计算,得到主缆各根索股下料长度,锚固区各索股的计算结果在图7中给出。

图7锚固区各索股下料长度修正计算结果对比
通过工程实例验算,对锚固区缆索各索股精细化结果对比可知,由于锚固区主缆各索股空间分布位置差异,主缆每股的无应力长度都不相同,部分索股计算值与中心索股长度差值较大,计算发现锚固区精确计算后与中心索股差值最大约4.9 cm,因此,在进行悬索桥主缆下料长度计算时,应考虑主缆结构的实际空间分布位置的差异性进行相对于中心索股长度的精细化修正计算,以保证计算结果的准确性。
5结语
(1) 建立缆索锚区主缆的局部坐标系,经过空间坐标变换,将任一索股的局部坐标统一至整体坐标系下,即可确定任一索股两端的相对位置坐标,精确求出缆索锚固区主缆各索股的下料长度。
(2) 论文以一座自锚式悬索桥为工程实例,研究了锚固区缆索下料长度精细化算法,研究发现由于各索股实际空间位置的差异性使各索股下料长度差异较大,有必要经过精细化算法进行相对于中心索股长度的修正计算后,再给出各索股的精确下料长度。
参考文献
[1]潘永仁,杜国华,范立础.悬索桥恒载结构几何形状及内力的精细计算[J].中国公路学报,2000(4):33-36.
[2]周孟波.悬索桥手册[M].北京:人民交通出版社,2003.
[3]文曙东,郑凯锋,栗怀广.空间索自锚式悬索桥线形精确计算方法研究[J].公路工程,2007,32(4):127-129.
[4]潘永仁,范立础.悬链线单元在悬索桥主缆下料长度计算中的应用[J].结构工程师,1998(3):22-24.
A Fine Calculation Method for the Anchorage Area of Suspension Bridge
WeiYuandong1,YangLinkai2
(1.Communications Design research institute Co., Ltd of Jiangxi Prov., Nanchang 330002, China)
2.Jiangxi highway research and design institute, Nanchang 330002, China)
Abstract:The unstressed length of the main cable is an important parameter that influences the finished state of bridge structure. A fine calculation method for the fabrication length of the main cable is proposed based on previous studies in this paper. Catenary cable element is utilized to simulate the main cable and calculate the unstressed length of the main cable center strand based on the target state of bridge structure. Then, the unstressed length of each main cable strand has been amended considering the actual spatial distribution of main cable at anchorage end. This calculation method has been verified by taking a suspension bridge with main span110m as an example.
Key words:suspension bridge; cable; fabrication length; fine calculation
收稿日期:2015-08-01
DOI 10.3963/j.issn.1671-7570.2015.06.007

