装配式斜交空心板梁桥的内力简化计算方法*

梁　栋　王云燕　马金龙　刘志强

(1.河北工业大学土木工程学院　天津　300401；　2.河北省土木工程技术研究中心　天津　300401)

装配式斜交空心板梁桥的内力简化计算方法*

梁栋1,2王云燕1马金龙1刘志强1

(1.河北工业大学土木工程学院天津300401；2.河北省土木工程技术研究中心天津300401)

摘要针对装配式斜交空心板梁桥的内力计算，推导了控制截面的内力折减公式，提出了将内力折减与铰接板法相结合的简化计算方法，并利用空间有限元和实桥测试等方法验证了该方法的正确性。

关键词装配式斜交空心板梁桥内力计算简化方法内力折减铰接板法

在桥梁建设中，常常由于桥位处的地形限制，或者由于高等级公路对线形的要求而将桥梁做成斜交。斜交空心板梁桥的桥轴线与支承线的垂线呈某一夹角，习惯上称此角为斜交角α。斜桥虽然有改善线形的优点，但其受力非常复杂。对于由多片空心板构成的装配式斜交桥，迄今仍没有成熟的荷载横向分布的简化计算方法。目前多借助计算机建立有限元模型得到。然而，有限元模型通用性较差，且不能真实模拟铰缝的力学状态，因此计算误差较大。

在理论分析方面，广大学者对简支斜交板的受力特点进行了大量研究，指出简支斜交板的跨中弯矩随斜交角的增大而减小[1-3]。但研究大多针对简支斜交的单梁[4](见图1)或整体式斜交板[5-6](见图2)进行。对于工程中常用的由多片空心板组成的装配式斜桥的内力分布，目前还没有成熟的简化计算方法。

图1　简支斜交单梁分析模型

图2　整体式斜交板分析模型

本文在前人研究的基础上，提出先考虑斜桥的内力折减，再利用铰接板法[2]计算斜交空心板梁桥各片梁的内力，以此得到装配式斜交空心板梁桥各片梁的内力。针对本文所提出的方法，利用空间有限元软件进行了对比分析，并通过实桥测试，验证了该方法的合理性。研究结论可为类似桥梁的设计及检测提供方便。

1装配式斜交空心板梁桥各梁内力的理论计算

1.1　斜交桥的内力折减

当集中力P作用于梁轴线上时，斜桥除了产生内力弯矩M外，还要产生转矩T，正是由于该转矩的存在使得跨中弯矩折减，求解该转矩是斜交桥内力折减的关键。

本文利用结构力学中的“力法”求解斜桥转矩。假定斜交桥横梁的抗弯刚度为无限大，抗扭刚度为0，则受载时主梁沿横梁方向的转动为0，而在垂直于横梁方向可自由转动，简化力学模型，见图3。按结构力学的内力规定，该力学模型中外力(转矩Ta，Tb)与反力(Ra，Rb)的正号见图3，弯矩(M)下侧受拉为正。根据以上假设，可将b端的扭转力(Tb)看作基本未知量X1，去掉扭转力对应的多余约束，将原结构转化成基本结构，见图4。

图3　简化力学模型

图4　基本结构

由上述推导可得简化力学模型x1位置处的弯矩值为

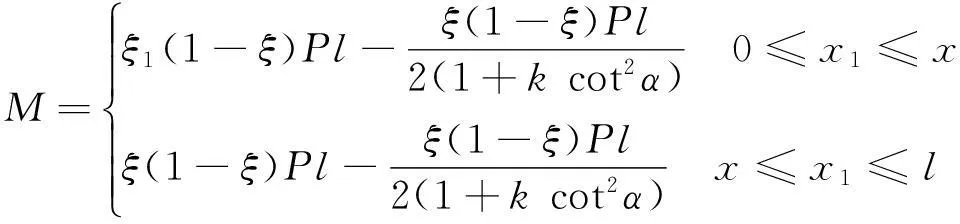
(1)

当ξ=ξ1=1/2时，即集中荷载P作用在跨中，计算跨中弯矩值为

(2)

由式(2)可见，斜交空心板梁桥，跨中截面作用集中力P时，跨中截面弯矩值随斜交角的增大而减小。

1.2　内力横向分布的铰接板法

针对装配式空心板梁桥，铰接板法[6]可将空间问题近似地转化成平面问题，在实际运用中具有简单、方便、快捷等优点。铰接板法的基本原理为：n条板梁组成的桥梁有(n-1)个欲求的未知铰接力峰值gi。当单位集中力P作用于1号梁时，根据力的平衡原理和力的互等定理，可得1号梁横向影响线的各竖标值为式(3)，再根据“力法”原理可得正则方程为式(4)。

(3)

(4)

式中：δik(i，k=1，2，…，n-1)为铰接缝k内作用单位正弦铰接力在铰接缝i处引起的竖向相对位移；δip(i=1,2,…,n-1)为外荷载P在铰接缝i处引起的竖向位移。由式(3)和(4)联立，解出各梁横向影响线的竖标值，相应的荷载横向分布系数如下。

(5)

1.3　装配式简支斜交空心板梁桥的内力简化计算方法

将内力折减的式(2)与铰接板法所得到的横向分布系数(5)结合起来以计算装配式斜交简支空心板梁桥的跨中弯矩，如下式。

(6)

本文采用有限元法与实桥测试相结合的方法，以验证式(6)的正确性。

2桥梁概况

为验证式(6)的合理性，本文针对下述桥梁进行了空间有限元分析和实桥测试。该桥跨径为20 m，简支空心板梁桥，斜交角为45°，设计荷载为公路-I级。该桥正面图和横断面布置分别见图5和图6。

图5　桥梁正面图

图6　桥梁跨中横断面图(单位：cm)

3空间有限元与简化计算方法的对比

针对上述桥梁，利用Midas/civil建立了其实体有限元模型，各梁之间的连接仅靠铰缝，铰缝也用实体单元模拟，铰缝的几何尺寸和材料特性与实际桥梁相同，见图7。简支梁桥梁高0.90 m，每块中板宽度1.19 m，边板宽度1.19 m，混凝土型号为C50，共9片梁，跨径为20 m。为进行对比分析，本文针对0°，15°，30°，45°，60°的倾斜角度进行了分析。集中荷载P取350 kN；1号梁弯扭刚度比k为1.482，2号梁弯扭刚度比k为1.177。

图7　实体有限元模型立面图

利用空间有限元和式(6)分别进行计算分析，可得出当1，2号梁跨中各自作用集中荷载P时，1，2号梁跨中截面应力值。计算结果见表1和图8。

表1　2种方法分别得到的跨中截面梁底应力　MPa

注：α为斜交角;相对误差δ为(|②-①|/①)×100%；δij表示荷载P作用于i号梁跨中时，j号梁跨中截面应力值的相对误差。

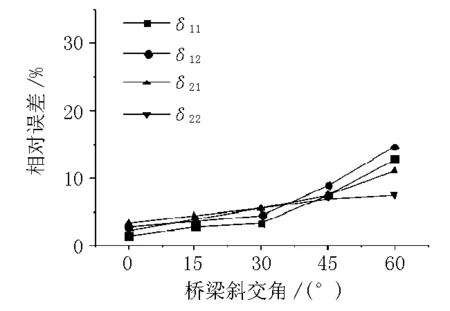
图8　相对误差趋势图

由表1和图8可见：当荷载P作用在1号梁跨中截面时，正桥1号梁相对误差值最小为1.40%，60°斜桥2号梁最大为14.63%；1号梁和2号梁的相对误差均随着斜交角增大而增大；斜交角度不大于45°时，相对误差在10%以内。当荷载P作用在2号梁跨中截面时，正桥2号梁相对误差值最小为2.18%，60°斜桥1号梁最大为11.12%； 1号梁和2号梁的相对误差均随着斜交角增大而增大；2号梁的相对误差均小于1号梁；斜交角度不大于45°时，相对误差在10%以内。

4实桥测试与简化计算方法的对比

4.1　测试概况

根据分析内容，对受力最大的1号梁、2号梁进行实桥检测。采用4辆350 kN的加载车(C1~C4)，加载车的前、中轴距为3.4 m，中、后轴距为1.4 m，车位布置见图9，图中截面B为跨中截面。试验挠度测点布置见图9(B1，B2分别为截面B上1，2号梁跨中梁底位置，A1，A2和C1，C2类同)，试验应变测点布置见图10。

图9　挠度测点布置和车位平面布置图(单位：cm)

图10　跨中应变测点布置及实桥布置图(单位：cm)

4.2　结果分析

本文分析了最大加载工况下1号梁与2号梁跨中B截面的挠度，实测值、式(6)计算结果与空间有限元模型计算结果的对比情况见表2，挠度向下为正；跨中B截面的梁底应力结果见表3，梁体下侧受拉为正。

表2　挠度测点检测结果　mm

表3　梁底应力测点检测结果　MPa

由表2和表3可见，本文所提出装配式斜交空心板梁桥的内力简化计算方法与空间有限元的计算结果非常相近，且与实桥测试结果吻合。

5结语

根据斜交空心板梁桥的结构特点，推导了其控制截面的内力折减公式，并结合铰接板法，提出了装配式斜交空心板梁桥的内力简化计算方法。理论分析及实桥测试结果表明，该方法具有很好的精度，在工程使用过程中简单、方便、快捷。

参考文献

[1]马占海.斜交板梁桥的横向受力理论计算与试验分析[J].交通科技,2015(2):40-41.

[2]姜基建,杨婧,王文龙.斜交箱梁桥静动力特性试验研究[J].交通科技,2015(1):1-4.

[3]何攀光.斜交涵长计算中平曲线半径影响的分析[J].交通科技,2006(1):10-12.

[4]李国豪.斜交结构的斜梁桥的荷载横向分布分析[J].同济大学学报:自然科学版，1994(4):395-400.

[5]赵书学.斜交桥梁的受力性能研究[J].公路交通科技,2004(9):57-59.

[6]黄平明.混凝土斜梁桥[M].北京：人民交通出版社，1999.

收稿日期：2015-05-28

DOI 10.3963/j.issn.1671-7570.2015.06.001

*天津市自然科学基金重点项目(12JCZDJC28900)资助