基于小波基的非线性抛物型系统模型预测控制
艾岭
(1.哈尔滨理工大学自动化学院,黑龙江哈尔滨 150080; 2.哈尔滨理工大学测控技术与仪器黑龙江省高校重点实验室,黑龙江哈尔滨 150080)
基于小波基的非线性抛物型系统模型预测控制
艾岭1,2
(1.哈尔滨理工大学自动化学院,黑龙江哈尔滨 150080; 2.哈尔滨理工大学测控技术与仪器黑龙江省高校重点实验室,黑龙江哈尔滨 150080)
针对一类由非线性抛物型描述的分布参数系统,研究了一种基于小波分解的模型降阶和预测控制方法。利用小波配点方法,分别将一阶和二阶空间偏导数投影到拟Shannon小波基上,不需要求解系统的主导极点,得到系统的低阶常微分方程逼近模型;采用前向Eular方法离散化时间变量,将得到的差分方程组模型作为系统的预测模型,选择标准二次优化性能指标,设计相应的非线性预测控制器;将此方法应用到由一个放置在反应器中的细长催化棒组成的传输-反应系统的温度场控制问题中,取得了满意的控制效果。
非线性抛物型系统;小波基;模型预测控制;棒式反应器;温度场控制
0 引言
目前,对于广泛存在于流体流动[1]、热传导[2-3]、空间分布化学反应[4-6]、柔性梁臂[7]等实际对象中的分布参数系统及其控制问题越来越受到学者和工程师的重视,已产生了许多可应用的模型逼近[8-9]和控制方法[10-11]。针对抛物型系统[12],一般采用(经验)主导基函数作为系统的空间基函数,将抛物型系统模型降阶为有限的常微分方程组进行处理[13]。由于需要首先求解主导基函数且采用的基函数是全局的,所以无法体现系统的局部特性,而择傅里叶级数[14]或其它正交多项式,如正交小波函数[15],它可以描述系统局部特性,空间基函数不依赖于对象特性,转换矩阵具有稀疏性,是一种理想的基函数。
预测控制是基于模型的先进控制算法[16],经过30多年的发展,已经成功应用在线性和非线性集中参数系统中[17],将其应用到分布参数系统是一种必然趋势。目前,已有学者对其进行研究并得到了有益的结果,将预测控制成功应用到分布参数系统的关键问题是找到描述分布参数系统的预测模型,而利用逼近模型转化为预测模型成为一个合理的思路。丁斗章等[18]应用Haar正交小波对分布参数系统进行逼近,提出了一种基于小波正交逼近的分布参数系统预测控制方法,获得了满意的效果。
本文选择拟Shannon小波尺度函数作为空间基函数,避免了Harr小波仅有一阶消失矩不适合逼近光滑函数和Shannon小波不具有紧支撑性的问题。基于小波配点法思想,应用离散化后的降阶模型作为预测模型,设计非线性预测控制器,并应用到一个棒式反应器温度控制问题中,说明所提算法的有效性。
1 问题描述
考虑一类抛物型系统的状态空间描述为[11]

具有如下形式边界条件,即

初始条件为

其中:X(x,t)=[X1(x,t)…Xn(x,t)]T表示状态向量,X(x,t)∈Hn[(α,β),Rn];X0(x)∈Hn[(α,β),Rn],Hn[(α,β),Rn]是定义在[α,β]区间上的n阶空间微分算子可积的无限维Hilbert空间,x∈[α,β]⊂R和t∈[0,∞)分别代表空间位置变量和时间变量;U(x,t)代表控制变量;y(x,t)代表输出变量;∂z2为空间微分算子;F(X)为关于X(x,t)的光滑函数; C、C1、C2、D1、D2、R1、R2为常值矩阵。
假设输出的测量点数量为2J+1,并且平均分布在区间[α,β]上,其中J为分解尺度,有界输入变量,设系统具有输入输出约束可表示为

其中:Umin,Umax分别表示U(x,t)的下限和上限; ymin,ymax分别表示y(x,t)的下限和上限。
2 预测模型
应用时空分解理论[8],将系统(1)中的时空变量展开的形式为

其中:Xj(xn,t)表示函数在点xn和时间t上的值,j表示小波尺度函数的层数;空间基函数选取拟Shannon小波尺度函数为[19]

一阶和二阶导数值分别如图1和图2所示。采用Eular前向差分法对时间偏导数进行离散,令Xj(xn,t)=Xj(xn,iΔt),i=1,2,…,则
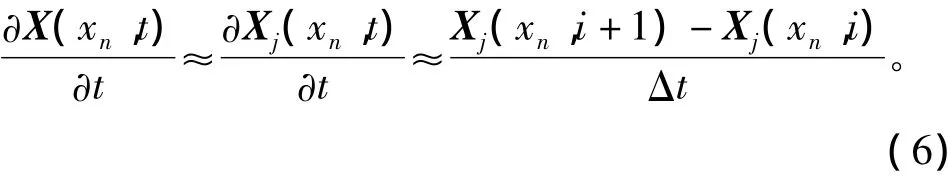
将式(3)、式(4)和式(5)代入式(1)可得


图1 拟Shannon尺度函数在区间[0,1]的一阶导数值Fig.1The first derivative of quasi-Shannon scaling function on the interval[0,1]

图2 拟Shannon尺度函数在区间[0,1]的二阶导数值Fig.2The second derivative of quasi-Shannon scaling function on the interval[0,1]
3 控制器设计
为了快速而平滑地得到系统设定值,定义参考轨迹为[20]

下面给出基于小波基的非线性预测控制算法。
算法1设计系统(1)在每一个采样时刻i=0,1,2,…的非线性预测控制器,分为4个步骤:
step1按式(10)定义系统最优参考轨迹;
step3求解关于U(·)∈UM(X(x,i))的最优控制问题,即

其中,P和M分别代表预测时域和控制时域;Q和R分别表示与受控变量的预测偏差相乘的权系数和与未来第i个控制变量相乘的权重对角矩阵;Umin和Umax分别表示的下限和上限。采用SQP算法对上述优化问题进行实时求解。
4 数值算例
考虑一个放置在反应器中的细长催化棒组成的传输-反应系统[21],如图3所示。
将物质A充进反应器入口,在催化棒上发生零阶放热催化反应为

由于反应放热,需要在催化棒周围放置冷却介质对系统进行冷却。
假设催化棒的密度、导热系数、比热和两端的温度均为常数,物质A在反应过程中是充足的。在这些假设下,催化棒一维无量纲温度场分布可由抛物型偏微分方程描述,即


βT,γ,βU分别表示反应热、活化能、导热系数,假设系统输出测量位置平均分布在轴向上,共有R= 2J+1个温度传感器,即

图3 催化棒示意图Fig.3Sketch map of catalytic rod
为了得到系统的真实值,应用有限差分法对系统进行求解,由于系统为一维抛物型系统,可以选择Matlab偏微分方程工具箱求解系统真实值。
取R=2J+1=24+1=17,利用式(3)、式(4)和式(5)得到系统(14)的P步向前预测值为

假设系统不存在控制约束,选择性能指标函数为

这里,P为预测时域,m为控制时域,分别取P=3,m=1,Q和R为权矩阵,Q=1 000×diag(1,…,1),R=diag(1,1),diag(·)为对角阵。
图4~图7分别给出了系统的控制变量、输出响应、不同位置的输出变化和空间稳态误差曲线,从仿真结果可以看出,本文所设计的控制器能够快速地(大概在0.2时间单位后)到达平衡状态(¯xss= 0),并且能够将系统的空间稳态误差在±0.01之间。

图4 控制器控制变量Fig.4Control variables
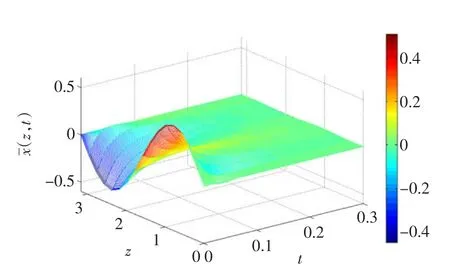
图5 输出响应Fig.5Curve of output response
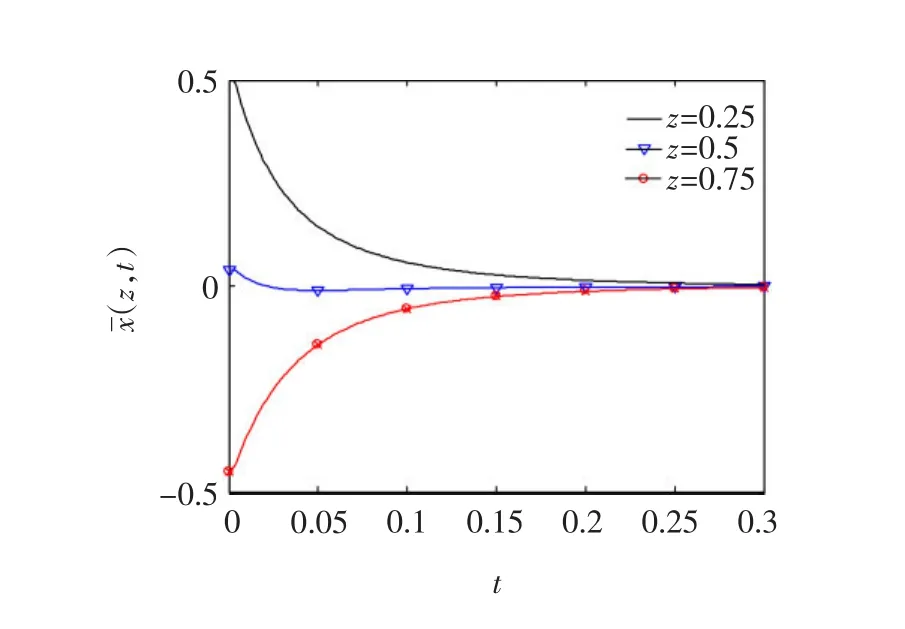
图6 不同位置的输出变化情况比较Fig.6Comparison of outputs at different locations

图7 稳态误差曲线Fig.7Curve of steady state errors
5 结论
针对参数化模型描述的非线性抛物型系统,利用小波配点法,选择拟Shannon小波尺度函数的一阶和二阶导数近似表示系统时空变量的空间偏导数,再利用前向Eular法离散化时间维常微分方程组,得到自回归差分方程组作为系统的预测模型,将控制问题转化为配置点上的预测控制问题,采用序列二次规划算法(SQP)在线求解滚动优化问题,将所提算法应用到棒式反应器的温度场控制问题中,取得了满意的控制效果。
[1]CANUTO C.Spectral methods in fluid dynamics[M].New York: Springer-Verlag,1988:1-10.
[2]BOSKOVIC D M,KRSTIC M,LIU Weijiu.Boundary control of an unstable heat equation via measurement of domain-averaged temperature[J].IEEE Transactions on Automatic Control,2001,12(46):2022-2028.
[3]李健,刘允刚.一类不确定热方程的自适应边界控制[J].自动化学报,2012,3(38):469-473.
LI Jian,LIU Yungang.Adaptive boundary control for a class of uncertain heat equations[J].Acta Automatica Sinica,2012,3 (38):469-473.
[4]华晨,李柠,李少远.分布参数系统的时空ARX建模及预测控制[J].控制理论与应用,2011,28(12):1711-1716.
HUA Chen,LI Ning,LI Shaoyuan.Time-space ARX modeling and predictive control for distributed parameter system[J].Control Theory&Applications,2011,28(12):1711-1716.
[5]WU W,CHEN C W.Measurement-based optimization and predictive control for an exothermic tubular reactor system[J].Industrial and Engineering Chemistry Research,2007,3:2064-2076.
[6]DUBLJEVIC S,CHRISTOFIDES P D,KEVREKIDIS I G.Distributed nonlinear control of diffusion-reaction processes[J].International Journal of Robust and Nonlinear Control,2004,14 (2):133-156.
[7]刘姝阳.基于分布参数模型机械臂操作柔性负载系统控制方法研究[D].长春:吉林大学,2013:4-13.
[8]LI H X,QI C K.Spatio-temporal modeling of nonlinear distributed parameter systems-a time/space separation based approach[M].New York:Springer,2011:13-50.
[9]窦磊.分布参数系统若干近似计算方法应用研究[D].南京:南京理工大学,2006:6-13.
[10]CHRISTOFIDES P D.Control of nonlinear distributed process systems:recent developments and challenges[J].AIChE Journal 2001,47(3):514-518.
[11]CHRISTOFIDES P D.Nonlinear and robust control of PDE systems:methods and applica-tions to transport-reaction processes[M].Boston:Birkhauser Boston Inc,2001:10-15.
[12]SMYSHLYAEV A,KRSTIC M.Adaptive control of parabolic PDEs[M].London:Princeton University Press,2010:1-2.
[13]LI H X,QI C K.Modeling of distributed parameter systems for applications:a synthesized review from time-space separation[J].Journal of Process Control,2010,20(8):891-901.
[14]FOURIER J.The analytical theory of heat[M].London:Cambridge University Press,2009:1-11.
[15]MAHADEVAN N,HOO K A.Wavelet-based model reduction of distributed parameter systems[J].Chemical Engineering Science,2000,55(19):4271-4290.
[16]席裕庚,李德伟,林姝.模型预测控制——现状与挑战[J].自动化学报,2013,39(3):222-236.
XI Yugeng,LI Dewei,LIN Shu.Model predictive control-status and challenges[J].Acta Automatica Sinica,2013,39(3):222-236.
[17]何德峰,丁宝仓,于树友.非线性系统模型预测控制若干基本特点与主题回顾[J].控制理论与应用,2013,30(3):273-287.
HE Defeng,DING Baocang,YU Shuyao.Review of fundamental properties and topics of model predictive control for nonlinear systems[J].Control Theory&Applications,2013,30(3):273-287.
[18]丁斗章.基于小波变换理论的分布参数系统预测控制[D].上海:华东理工大学,2008:1-15.
[19]WEI G W.Quasi wavelets and quasi interpolationg wavelets[J].Chem Phys Lett,1998,296(6):215-222.
[20]席裕庚.预测控制[M].2版.北京:国防工业出版社,2013: 4-9.
[21]REN Y Q.Multi-variable fuzzy logic control for a class of distributed parameter systems[J].Journal of Process Control,2013,23(1):351-358.
(编辑:张诗阁)
Model predictive control for nonlinear parabolic system using wavelet base
AI Ling1,2
(1.School of Automation,Harbin University of Science and Technology,Harbin 150080,China;
2.The Higher Educational Key Laboratory for Measuring&Control Technology and Instrumentations of Heilongjiang Province,Harbin University of Science and Technology,Harbin 150080,China)
For a class of nonlinear parabolic distributed parameter systems,model reduction and predictive control method were investigated.First,the first order and second order spatial partial derivative were projected to quasi-Shannon wavelet using wavelet collocation method respectively,eliminating the need of knowledge of solution of dominant pole of the system.The correspondent lower order model was obtained.A group of ordinary differential equations obtained through Eular’s discretizing time variable was selected as the predictive model of the system,standard quadratic optimization performance index was selected,and the corresponding nonlinear predictive controller was designed.This method was applied to the transfer-reaction system of catalytic rod,and simulation results indicate that the proposed method meets the requirements of system control.
nonlinear parabolic system;wavelet base;model predictive control;catalytic rod;temperature field control
10.15938/j.emc.2015.01.013
TP 273
A
1007-449X(2014)11-0090-06
2014-01-20
国家自然科学基金(61074127)
艾岭(1982—),男,博士,研究方向为分布参数系统,预测控制等。
艾岭

