一种SVPWM过调制算法及其在两电平逆变器中的应用

吴晓新，柳巍，阮毅，张笠君

（1.上海大学机电工程与自动化学院，上海 200072;2.南通大学电气工程学院，江苏南通 226019）

一种SVPWM过调制算法及其在两电平逆变器中的应用

吴晓新1，2，柳巍1，阮毅1，张笠君1

（1.上海大学机电工程与自动化学院，上海 200072;2.南通大学电气工程学院，江苏南通 226019）

过调制能够有效地提高逆变器的输出基波电压，传统的空间矢量PWM过调制算法需要经过复杂的实时计算或查表，不易于实现。针对此问题，研究一种过调制算法，不需要经过复杂的运算和查表，易于实现，能够使逆变器从线性调制区平滑地过渡到六阶梯波工作区，并且输出电压谐波含量低。在两电平逆变器矢量控制系统上对过调制算法进行了实验。理论分析和实验结果表明该算法具有输出电压谐波含量低和实现简便的优点，适合应用于矢量控制系统中。

空间矢量PWM;过调制;电压源逆变器;矢量控制;异步电机

0 引言

在交流传动领域，电压源逆变器占据主流地位，而SVPWM是电压源逆变器调制策略的主流，上个世纪末，对SVPWM的研究主要集中在线性调制区，线性区仅能够将输出电压提高到方波工况时的90.69%，为了获得更大的输出电压，逆变器必须工作在过调制区，直至达到方波工况。最近十几年，各种过调制技术开始得到研究［1－3］，在所有的过调制研究中，大都集中在作为电机驱动的逆变器，应该注意的是，过调制会引入低次谐波和高的THD，并且越接近六阶梯波工作模式，谐波含量越高，波形质量越差。进入过调制区后，输出电压将出现严重畸变，影响电机输出转矩。所以过调制研究关注的重点是谐波含量的多少以及实现的难易程度上。

目前提出的空间电压矢量过调制算法有很多种，算法的难易程度各不相同。文献［4］提出的前馈方法将过调制区划分为两个区间，分别采用不同的过调制模式，离线计算得到数值存放在表格中，通过在线查表的方式获得修正后的电压矢量。文献［5］对已有的双调制区算法进行改进，减少了计算量，但高次谐波含量更高。文献［6］将两个过调制区看成一个区，通过一种算法，使输出电压从线性区过渡到六阶梯波，它的算法简单易于实现，但比以前方法有更高的谐波含量。文献［7］给出了在过调制区如何对逆变器输出电压谐波含量分析的方法，可为以后的过调制算法进行性能指标分析。文献［8］给出了一个修正函数，使电压矢量的幅值和相角变化平稳，利用修正函数的连续性和对称性降低高频谐波成分，并且使线性调制区和过调制统一为一个调制区。但修正函数参数确定较为繁琐，且没有给出实验验证。

本文研究了一种SVPWM过调制算法，易于数字实现，经过傅立叶分析，逆变器输出电压谐波含量低，总谐波畸变得到改善。最后本文给出了实验结果，证明了理论分析的正确。

1 SVPWM方法

电压空间矢量定义为

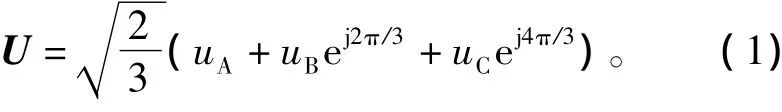
式中:uA、uB、uC为三相电压的瞬时值;U为合成的电压矢量。两电平逆变器一共可输出8个电压矢量，6个非零矢量长度均为。6个非零矢量将空间分为6个扇区，每个扇区60°，非零扇区顶点相连组成一个正六边形，如图1所示。

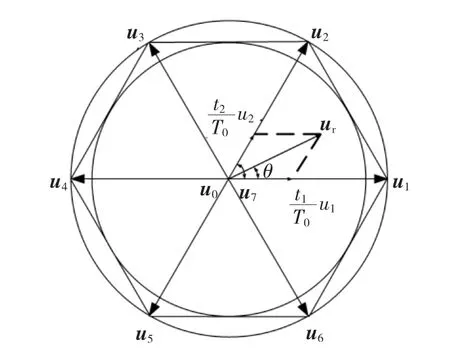
图1 空间电压矢量图Fig.1Voltage space vector diagram

1.1 线性调制区

当参考电压矢量ur的轨迹位于正六边形内切圆内部时，参考电压矢量可由相邻的2个基本电压矢量线性组合而成，内切圆内部为线性调制区。2个基本矢量的作用时间为t1、t2，其表达式为

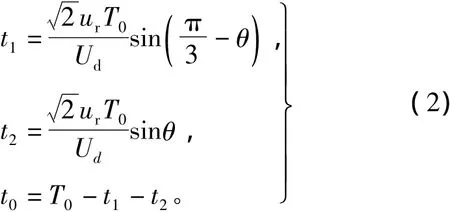
式中:t0为零矢量的作用时间;T0为SVPWM的开关周期。

线性调制区的特点是输出的电压矢量在角度和幅值上保持连续性。当参考电压矢量幅值超过内切圆半径时，逆变器就进入过调制状态，输出的电压波形也将产生畸变。

2 过调制策略

2.1 过调制I区策略

过调制I区内的参考电压矢量幅值位于正六边形内切圆和外接圆之间，即参考电压矢量轨迹部分在正六边形内部，部分在正六边形外部。

在1/4周期内，电压矢量轨迹如图2所示。ur为参考电压矢量轨迹，当参考电压矢量在六边形内部时，实际电压矢量和参考电压矢量相等。在六边形外部时，用六边形上不同相位和不同幅值的电压矢量来代替参考电压矢量。OA、OB为基本电压矢量，以OA为起始位置，如参考电压矢量在OP位置时，过P点分别作OA、OB的平行线，交OB、OA于G、H点，组成平行四边形OHPG，平行四边形与正六边形的边AB交于E、F点。当OP的相角小于时，以电压矢量OF为实际电压矢量，代替参考电压矢量OP，当OP的相角大于时，以电压矢量OE为实际电压矢量。

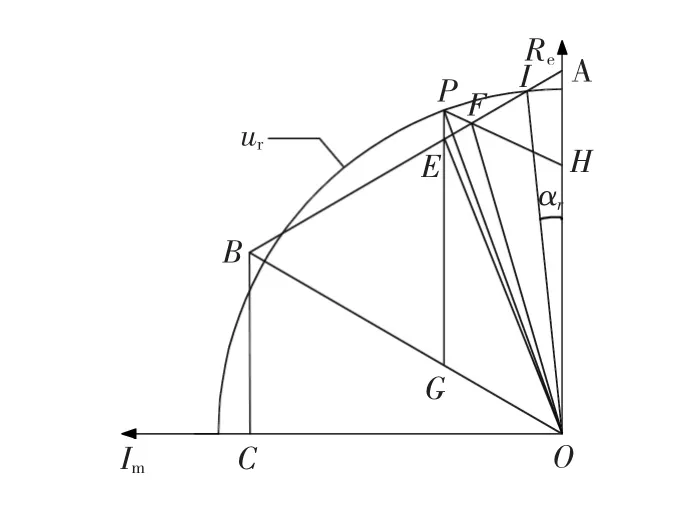
图2 过调制I区Fig.2Over modulation Region I

2.2 过调制II区策略

过调制II区内的参考电压矢量幅值位于正六边形外接圆之外。在1/4周期内，电压矢量轨迹如图3所示，当参考电压矢量的相角与某个基本电压矢量相角之差小于保持角αh时，输出电压矢量保持为该基本电压矢量，当相角之差大于保持角αh时，则采用与过调制I区相同的方法进行处理。过调制II区是利用六条基本电压矢量来增大输出电压基波的幅值，保持为基本电压矢量的时间越长，输出的电压基波幅值就越大，含有的低次谐波含量就更高，当每个基本电压矢量作用的时间为1/6周期时，逆变器就工作于六阶梯波状态。

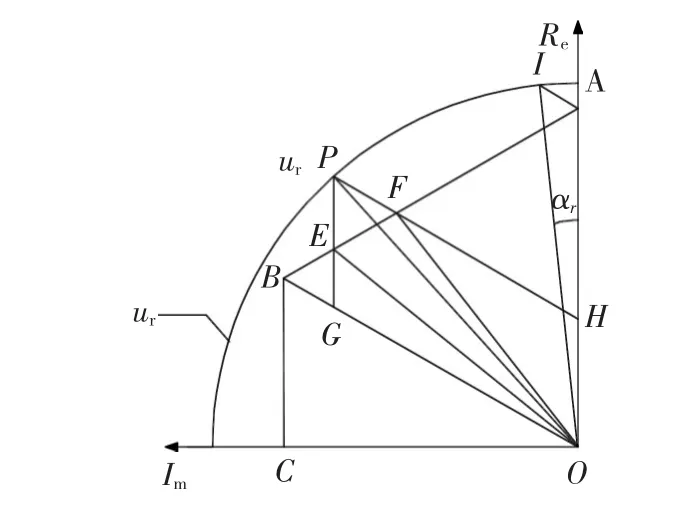
图3 过调制II区Fig.3Over modulation Region II

3 输出波形分析

3.1 过调制I区

定义电压利用率

式中:u1为输出相电压的基波幅值;UDC为逆变器的直流母线电压;为六阶梯波作用下的相电压基波幅值，因此电压利用率0≤M≤1。

参考电压矢量轨迹在1/4周期内如图4所示，图中粗实线为修正后的电压矢量轨迹。由于电压矢量在实轴（即A相相轴）的投影是A相电压瞬时值倍［10］，所以过调制I区中的修正后的电压矢量在实轴上的投影如图4所示，其中αr为参考电压矢量轨迹和正六边形边界交点与原点形成的边与扇区边的夹角，αr与ur的关系为投影值的表达式为

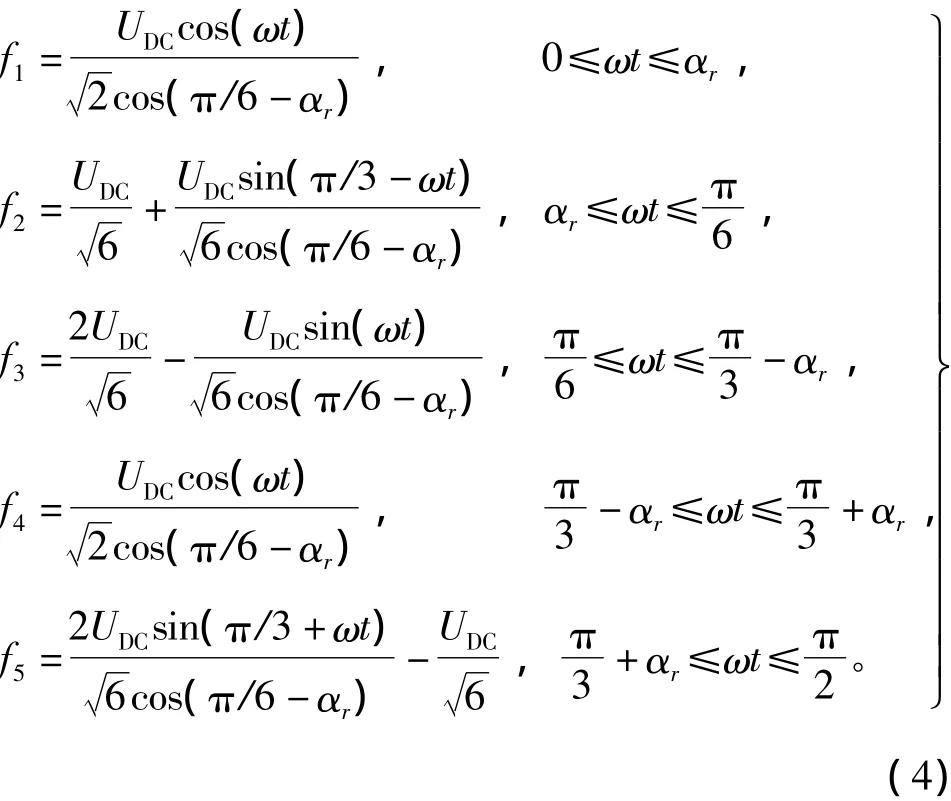
式中，ω为参考电压矢量ur的旋转角速度。

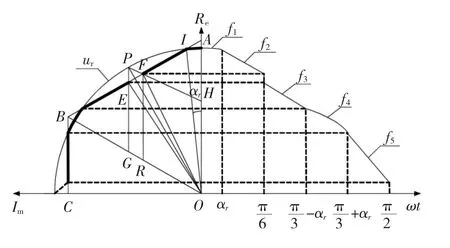
图4 过调制I区电压矢量轨迹Fig.4The trajectory of voltage vector in over modulation Region I

逆变器输出的相电压基波成分可由傅立叶分解得到，表达式为

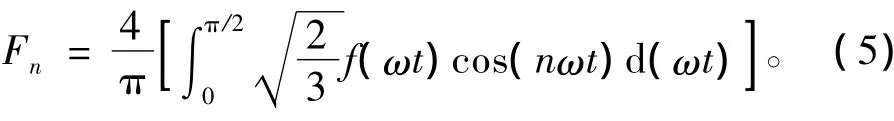
对式（4）进行傅里叶分解，求出基波幅值，代入式（3）可得电压利用率M。当，即参考电压矢量幅值为内切圆半径时，M=0.907。当，即参考电压矢量幅值为外接圆半径时，M=0.967。所以过调制I区电压利用率范围是0.907≤M≤0.967。

3.2 过调制II区

过调制II区中的修正后的电压矢量在实轴上的投影如图5所示，其中αh为保持角，αh与ur的关系为，投影值表达式为

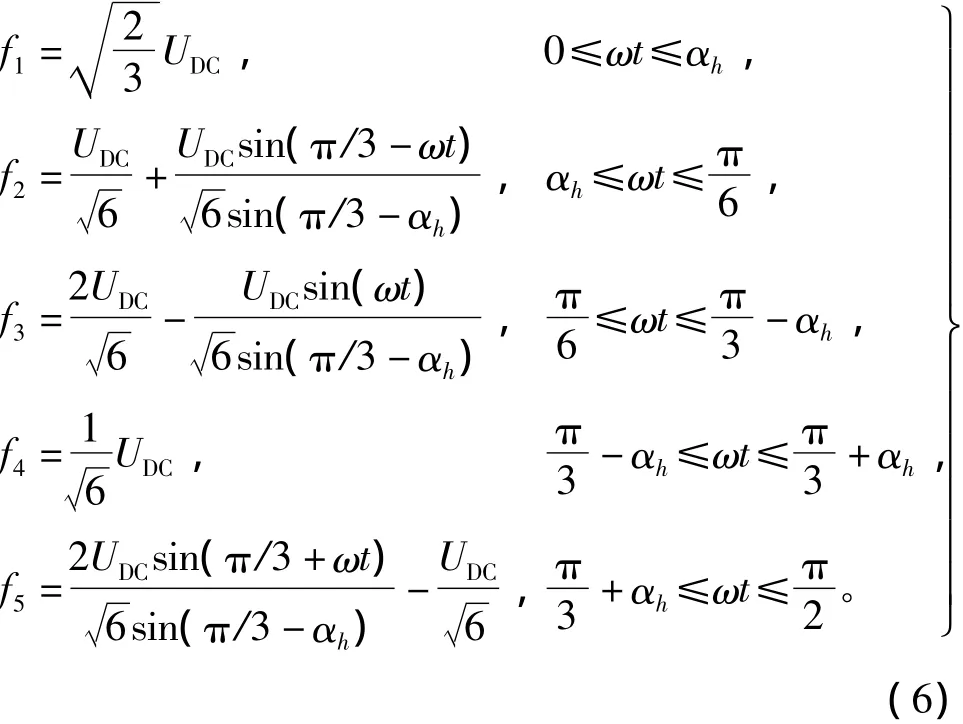
式中，ω为参考电压矢量ur的旋转电角速度。

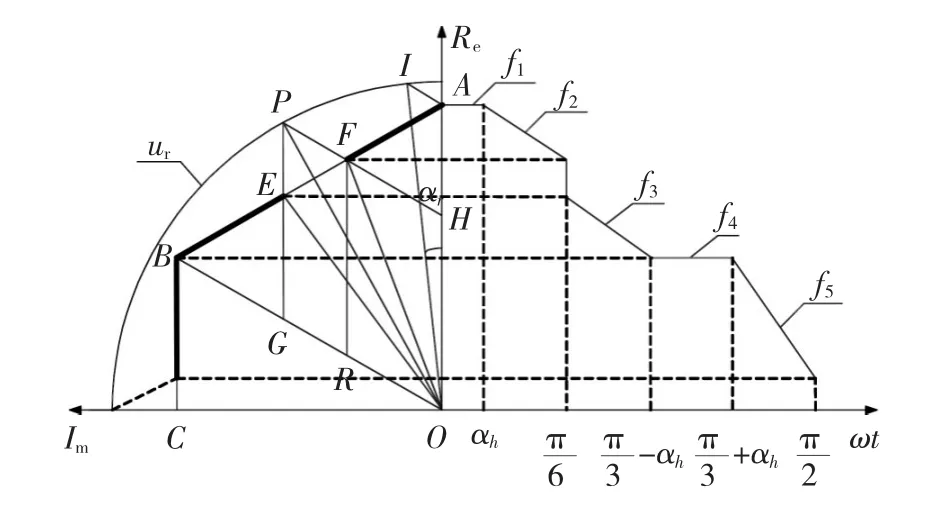
图5 过调制II区电压矢量轨迹Fig.5The trajectory of voltage vector in over modulation Region II

4 谐波分析

不考虑由于PWM调制产生的谐波，只考虑由于过调制引入的谐波。逆变器输出相电压中的各次谐波成分可由傅立叶分解得到［7］，表达式为式（5）。由于输出电压波形是正负半周期对称的，所以不含偶次谐波，根据电压型逆变器的工作原理，逆变器输出线电压中不含3次谐波，所以本节主要分析对逆变器性能影响较大的5、7、11、13次谐波。把式（4）和式（6）分别代入式（5），得到过调制I区和II区的各次谐波成分，结合式（3），可得谐波幅值与电压利用率M的关系。

用数值计算的方法画出基波电压幅值u1和参考电压矢量幅值ur的关系曲线，如图6所示。随着参考电压矢量幅值的增加，相电压基波幅值也相应的增加，并且是平滑地从过调制I区过渡到II区，最终达到基波电压幅值u1表达式为

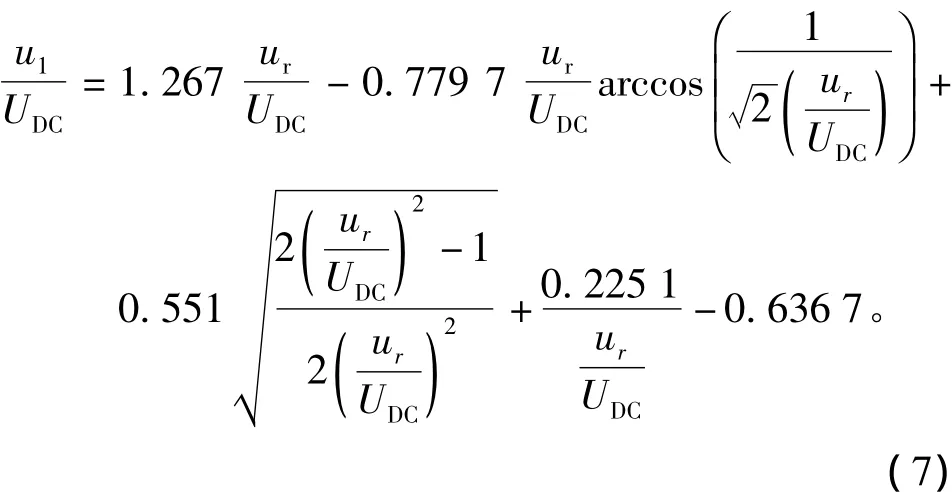
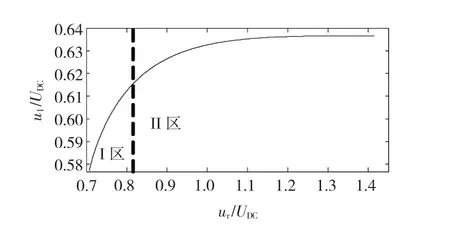
图6 基波电压幅值与参考电压矢量幅值关系Fig.6Relationship between u1and ur

图7为各次谐波电压幅值与电压利用率M的关系图。随着电压利用率的增加，各次谐波含量均逐渐增加，直到六阶梯波状态时达到最大值。

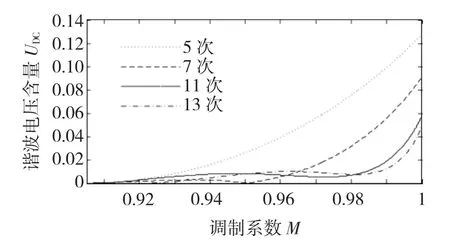
图7 谐波电压幅值与电压利用率M关系Fig.7Relationship between harmonic voltage amplitude and M

定义总谐波畸变率THD，记作

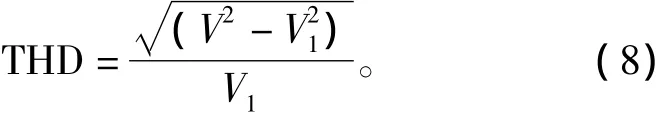
其中，V，V1分别为输出的相电压有效值和相电压基波分量有效值。图8画出了THD与电压利用率M的关系曲线，THD随着M的增加而增加。为了便于与其他算法进行比较，文献［10］中的基波电压幅值线性控制方法和文献［9］中的单调制区方法的THD曲线也画在图中。在整个过调制范围内，本文算法的THD值都比其他两种算法低，可以看出本文算法在谐波含量指标方面要优于其他两种算法。

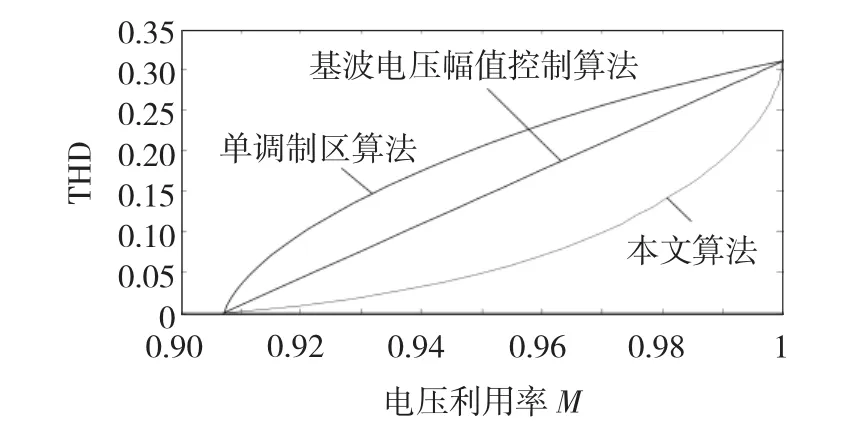
图8 THD与电压利用率M关系Fig.8Relationship between THD and M

5 仿真分析

为了验证本文过调制控制策略的有效性，在Matlab/Simulink环境下搭建了仿真模型进行仿真分析。仿真模型中异步电机参数与实际电机参数相同，为额定功率为3 kW;额定电压为380 V;额定电流为6.9 A;额定转速为1 400 r/min;额定频率为50 Hz;极对数为2。

图9为直流母线电压出现波动后，线电压和线电流的暂态响应。可以看出尽管直流母线电压下降，但逆变器过调制能保持输出电压基波分量不变。

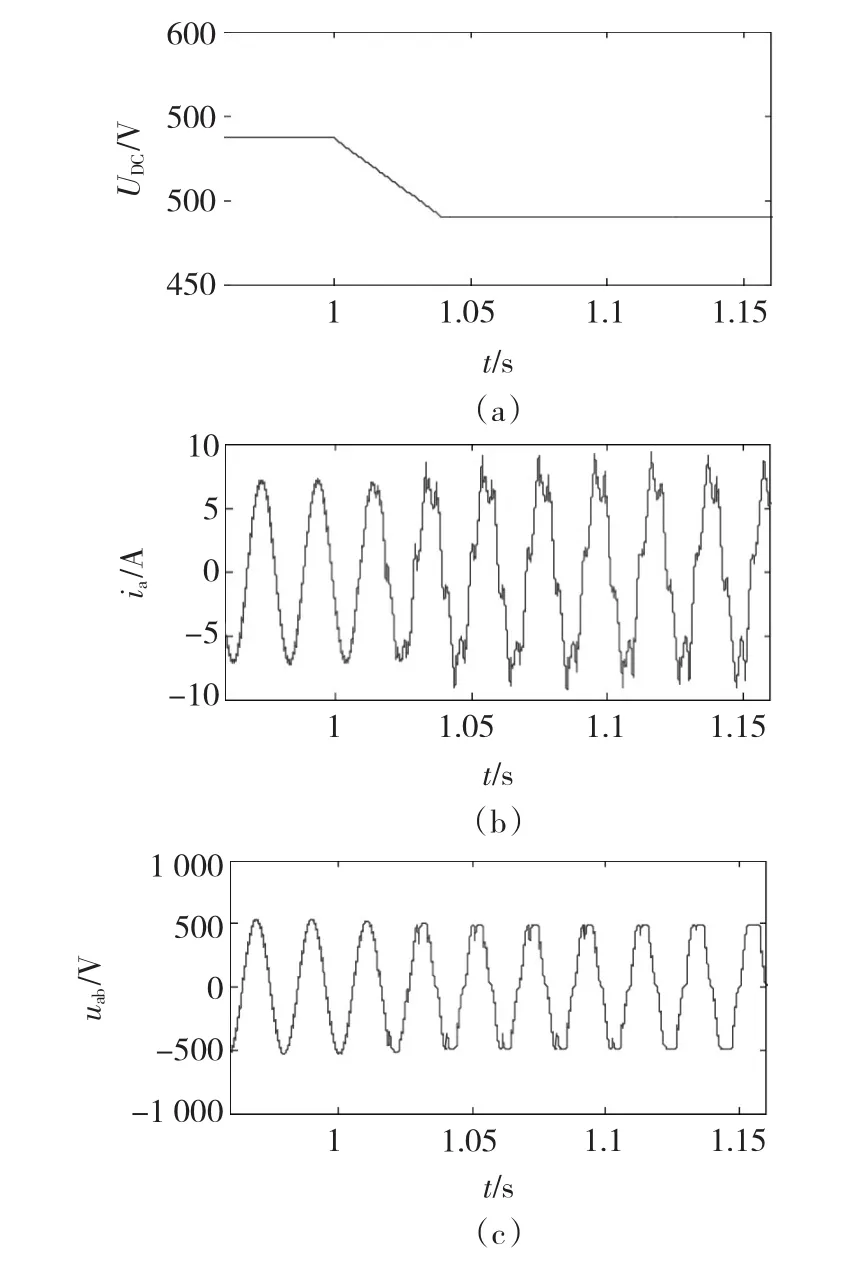
图9 直流母线电压跌落时的瞬态响应Fig.9Transient responses for dc-link voltage disturbance

图10为电压利用率为1时，线电压经过FFT变换后的各次谐波成分，从图10中可以看出，线电压中没有偶次谐波和3的倍次谐波，谐波以5、7、11、13次为主，且幅值大小符合理论计算。

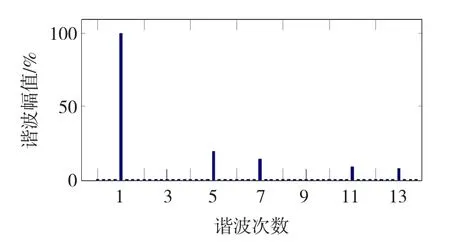
图10 M=1时，线电压频谱分析图Fig.10Harmonic spectra by FFT，normalized to fundamental component at M=1

6 实验结果

为了进一步验证本文提出的过调制算法的有效性，通过实验进行了验证。主电路采用IGBT模块构成一个三相电压源逆变器，开关频率为4 kHz，控制系统以dsPIC30F6010A为控制核心，采用矢量控制策略，异步电机参数如上节所述。

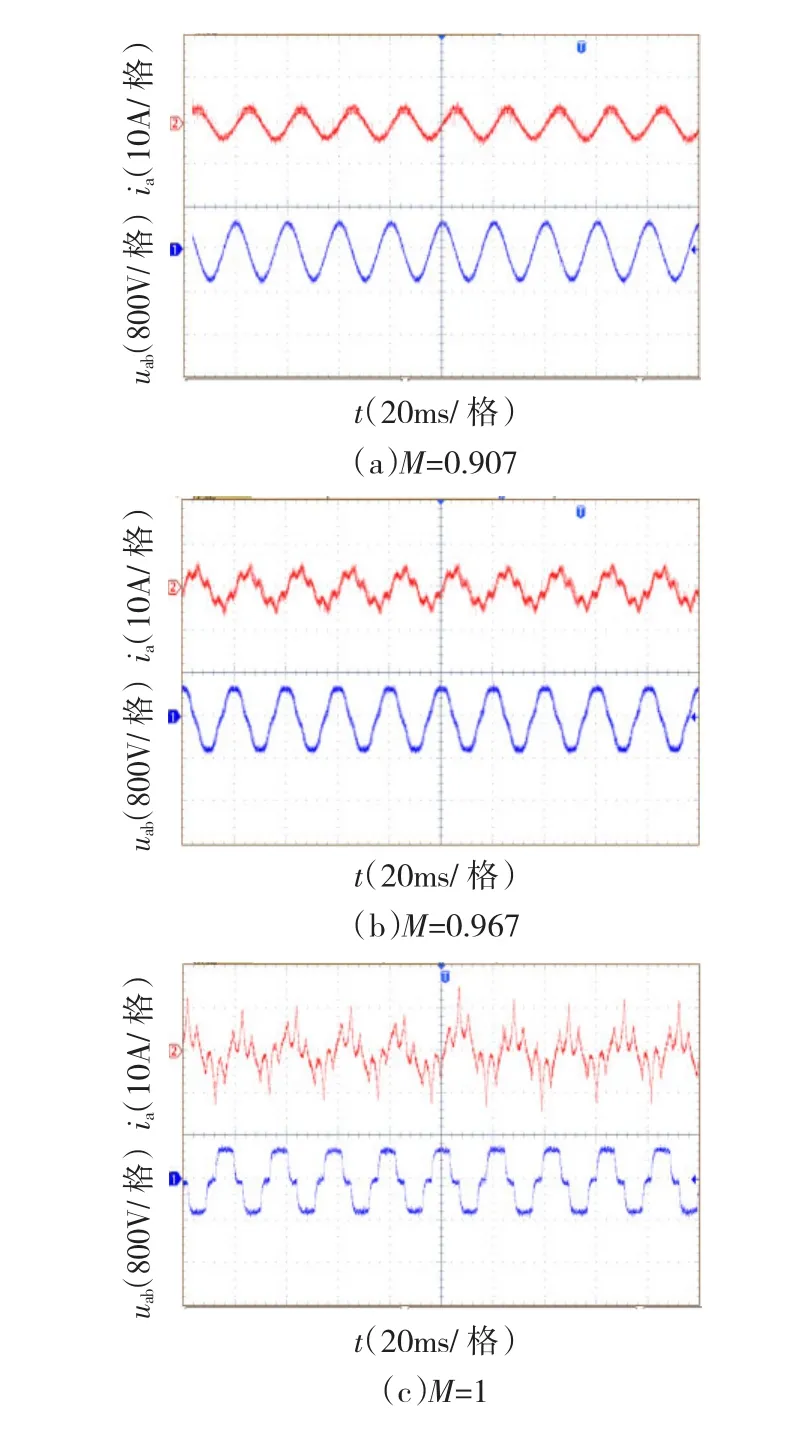
图11 线电压和线电流波形Fig.11Line voltage and line current waveforms

首先进行过调制算法的验证试验，图11为不同电压利用率下的线电压和线电流波形。图11（a）对应最大线性调制，此时电压和电流都是正弦波。图11（b）对应过调制I区和II区的分界处，电压和电流都发生一定程度的畸变。图11（c）为系统处于六阶梯波状态，电压和电流畸变最大。

图12为电压利用率从0.907增加到1时，线电压和线电流的动态响应曲线。可以看出电流不会突变，而是平滑地变化，说明系统动态过渡过程良好，图12为系统处于过调制状态的波形，所以谐波较大。

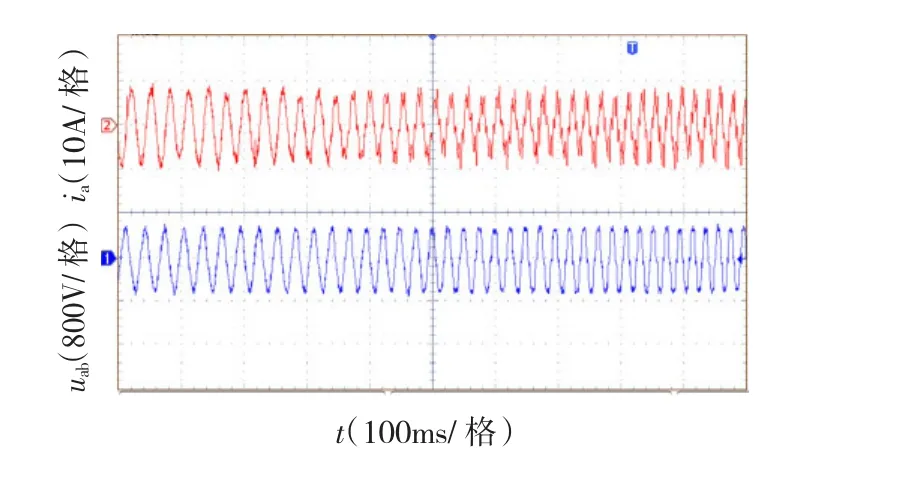
图12 电压利用率增加时的瞬态响应Fig.12Transient responses for M increases

直流母线电压降低时，逆变器通常工作在过调制区。图13为空载时直流母线电压从500 V降低到437 V时，系统从线性区过渡到过调制区，电压利用率增加，使输出电压基波含量不变，系统处于稳定状态。

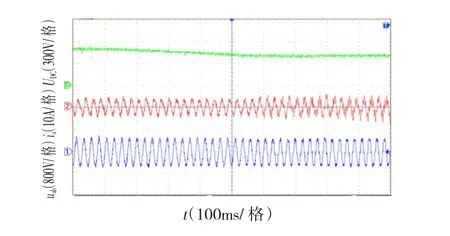
图13 直流母线电压跌落时的瞬态响应Fig.13Transient responses for dc-link voltage disturbance

7 总结

本文提出了一种SVPWM的过调制算法，能够使直流电压利用率达到1。详细分析了该算法的基本原理，通过傅里叶分析发现，该算法含有较低的谐波含量和THD。

实验表明，该算法能够使系统从线性调制区平滑地过渡到六阶梯波状态，不需要复杂计算和查表，可以方便地对现有系统进行改进，将该算法应用于矢量控制系统中，获得了满意的效果。

［1］吴芳，万山明，黄声华.一种过调制算法及其在永磁同步电动机弱磁控制中的应用［J］.电工技术学报，2010，25（1）:58－63.

WU Fang，WAN Shanming，HUANG Shenghua.An overmodulation algorithm and its application in pmsm drive with flux-weakening control［J］.Transactions of China Electrotechnical Society，2010，25（1）:58－63.

［2］TRIPATHI A，KHAMBADKONE A M，PANDA S K.Direct method of overmodulation with integrated closed loop stator flux vector control［J］.IEEE Transactions on Power Electronics，2005，20（5）:1161－1168.

［3］王建渊，王琦，钟彦儒.一种用于三电平逆变器的双模式过调制策略［J］.电机与控制学报，2012，16（6）:30－36.

WANG Jianyuan，WANG Qi，ZHONG Yanru.One strategy of two-model over modulation for three-level inverter［J］.Electric Machines and Control，2012，16（6）:30－36.

［4］HOLTZ J，LOTZKAT W，KHAMBADKONE A M.On continuous control of pwm inverters in the over-modulation range including the six-step mode［J］.IEEE Transactions on Power Electronics，1993，8（4）:546－553.

［5］S VENUGOPAL，G NARAYANAN.An overmodulation scheme for vector controlled induction motor drives［C］//Proceedings of IEEE Power Electronics，Drives and Energy Systems，2006，1－6.

［6］ANDRKS DIAZ，ELIAS G STRANGAS.A novel wide range pulse width overmodulation method［C］//Proceedings of IEEE Applied Power Electronics Conference and Exposition，2000，556－561.

［7］S BOLOGNANI，M ZIGIIOTTO.Space vector fourier analysis of SVM inverters in the overmodulation range［C］//Proceedings of IEEE Power Electronics，Drives and Energy Systems for Industrial Growth，1996，319－324.

［8］ILIOUDIS C Vasilios，MARGARIS I Nikolaos.A novel SVPWM overmodulation technique based on voltage correcting function［C］//oceedings of IEEE Power Electronics for Distributed Generation Systems，2012，682－689.

［9］BOLOGNANI S，ZIGLIOTTO M.Novel digital continuous control of SVM inverters in the overmodulation range［J］.IEEE Transactions on Industry Applications，1997，33（2）:525－530.

［10］张立伟，刘钧，温旭辉，等.基于基波电压幅值线性输出控制的SVPWM过调制新算法［J］.中国电机工程学报，2005，25 （19）:12－18.

ZHANG Liwei，LIU Jun，WEN Xuhui，et al.A novel algorithm of SVPWM inverter in the overmodulation region based on fundamental voltage amplitude linear output control［J］.Proceedings of the CSEE，2005，25（19）:12－18.

（编辑:刘素菊）

SVPWM over-modulation algorithm and its application in two-level inverter

WU Xiao-xin1，2，LIU Wei1，RUAN Yi1，ZHANG Li-jun1
（1.Electromechanical Engineering and Automation College，Shanghai University，Shanghai 200072，China; 2.School of Electrical Engineering，Nantong University，Nantong 226019，China）

The fundamental voltage of the inverter can be effectively improved with over-modulation.It needs complex real-time calculation or look-up table for traditional SVPWM over-modulation algorithm，which is not easy to implement.A over-modulation algorithm for SVPWM inverters is presented，which was simple and suitable for digital implementation.The inverter transited from the linear operation to the six-step operation smoothly.The harmonic components and the total harmonic distortion of the output voltage were analyzed.The over-modulation algorithm experiments were carried out on the two-level inverter vector control system.Theoretical analysis and experimental results verify that the algorithm is convenient and feasible，with low THD.

space vector PWM（SVPWM）;over-modulation;voltage inverter;vector control system;induction motors

10.15938/j.emc.2015.01.011

TM 464

A

1007－449X（2015）01－0076－06

2013－06－14

国家自然科学基金（61305031）;江苏省自然科学基金（KB2012227）

吴晓新（1978—），男，博士研究生，研究方向为异步电机矢量控制;

柳巍（1988—），男，硕士，研究方向为电力电子与电力传动;

阮毅（1955—），男，教授，博士生导师，研究方向为电力电子与电力传动;

张笠君（1990—），男，硕士，研究方向为异步电机无速度控制。

阮毅