开关磁阻电机多目标协同优化设计

宋受俊，葛乐飞，张蔓

（西北工业大学自动化学院，陕西西安 710072）

开关磁阻电机多目标协同优化设计

宋受俊，葛乐飞，张蔓

（西北工业大学自动化学院，陕西西安 710072）

针对开关磁阻电机存在多变量、强耦合、高非线性等特点以及传统方法较难快速而准确地获得其最优设计方案的问题，引入了多目标协同优化设计方法。对协同优化算法进行了改进，提出了新型动态松弛因子法以及最优保留策略，在保证算法收敛性的同时，提高了其收敛速度及精度。以效率及转矩脉动为目标，利用改进型协同优化算法对开关磁阻电机的初始设计方案进行了优化，得到了关键几何尺寸和控制参数的全局最优取值。针对优化方案功率密度和热负荷较高的问题，设计了一个定、转子双水冷系统，并通过集中参数热网络模型证明了电机主要部位温度在工程允许范围之内。分析结果表明，改进型协同优化算法的引入达到了提升电机效率并降低其转矩脉动的目的。

磁阻电机;多目标优化;协同算法;动态松弛法;最优保留策略;水冷系统;热网络模型

0 引言

作为一种极具竞争力的新型机电一体化设备，开关磁阻电机（SRM）具有结构简单坚固、调速范围宽、起动转矩大、控制灵活、可靠性较高、成本较低以及适应恶劣环境等诸多性能优势［1］，在航空工业［2］、电动汽车［3］、新能源发电［4］、伺服系统［5］，家用电器［6］等领域具有巨大的发展潜力和广阔的应用前景。然而，较低的运行效率、显著的转矩脉动极大地限制了SRM的进一步应用及推广。如何快速而准确地对其进行优化设计及控制以突破技术瓶颈，一直是国内外学者研究的热点问题。

开关型供电模式以及铁心磁密的高度饱和使得SRM驱动系统具有多变量、强耦合、高非线性等特点，给设计及控制造成了较大的困难［7－8］。国内外学者在该领域做了大量的工作，取得了显著进展，有效提升了SRM的性能［9－11］，部分学者在其工作中引入了优化思想［12－14］，为SRM的设计提供了新途径。

协同优化算法（COA）是由斯坦福大学的Ilan M.Kroo等学者提出的，非常适用于求解多学科复杂优化问题，在航空航天［15］、电力传输［16］、生产配送［17］等领域得到了广泛应用。

SRM的优化设计过程涉及到效率、转矩脉动等多个目标以及几何尺寸、控制参数等多个变量，是一个复杂的多维优化问题，而COA是一种层级优化思想，可以通过学科划分有效降低所求解问题的复杂度。另外，研究发现SRM优化可以转化为只有定、转子极弧耦合的优化问题，而COA非常适用于求解学科内变量远远多于学科间耦合变量的松散耦合问题。

本文在SRM的优化设计及控制中引入了COA，在一定的优化目标及约束下，得到了关键几何尺寸和控制参数的全局最优解，在保证外形尺寸不变的前提下，提高了效率，减小了转矩波动，从而验证了方法的有效性，显示了其性能优势。

除电磁特性外，热特性是电机设计中需要考虑的另一个重要方面。本文通过热特性分析发现所得优化方案的热负荷较高，温升较大，有必要设计散热系统。

目前，电机热特性分析方法主要分为数值法和解析法两类。有限元法（FEM）是数值法的代表［11］，三维FEM的准确度较高，但处理过程复杂，计算量大，较为耗时。集中参数热网络法（LPTN）是最常使用的热特性解析计算方法［18］，与FEM相比，LPTN能够在保证相当精度的同时，提高计算速度，且具有较强的灵活性。

本文设计了一个定、转子双水冷系统，并利用LPTN对优化方案进行了校核，结果证明电机各主要部分的温度均在工程允许范围之内。

1 协同优化算法及其改进

COA是一种按学科对复杂问题进行分解、协调以及综合优化的方法，其基本思想为将复杂问题分解成一个系统级优化问题和若干个学科级优化问题，首先通过各学科的独立并行运算，在满足各自局部约束的前提下实现自身优化。而后，学科级优化结果和约束信息被反馈至系统级，并通过系统级优化使学科间的不一致性达到最小。经过多次迭代，直到达到最大优化代数或连续几代适应度值的均方差小于某一个正实数，最终得到一个符合学科间一致性约束的系统最优解。其算法框架如图1所示。其中，F（Z）为系统级目标函数，Z为系统级优化变量构成的向量，Zj为系统级第j维优化变量;Ji（Z）为系统的第i个约束条件，亦即第i个学科的目标函数;gi（Xi）为第i个学科的约束条件，Xi为由第i个学科中的优化变量构成的向量，Xij为第i个学科中的第j维优化变量;M为系统级优化变量的维数，N为划分的学科数;αij为一个系数，若第i个学科的第j维变量与系统变量耦合，则其值为1，反之为0。

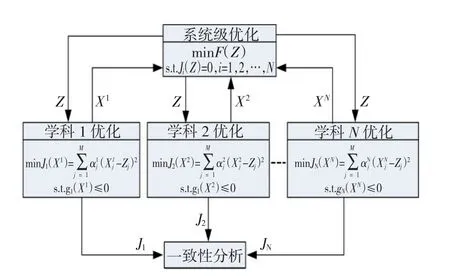
图1 COA算法框架Fig.1Framework of COA

在传统COA中，由于系统级一致性约束函数与优化变量没有直接关系，导致系统级约束函数可能是非光滑的，甚至是不连续的，而且可能产生局部最优，降低了算法的鲁棒性。国内外学者对此提出了多种改进方法，如系统级敏感度法、响应面法、近似子空间法、松弛约束法等。其中松弛约束法是较常用的方法，但松弛因子ζ的选取具有主观性，缺少理论依据。ζ值太小，减小了可行解的搜索范围，太大又会使一致性约束失去意义。文献［19］提出了一种动态松弛算法，并对动态松弛因子的选取方法进行了研究;文献［20］采用“或”逻辑把两个学科中以为半径的搜索空间叠加在一起，在一定程度上增强了COA的全局搜索能力。但上述方法均只适用于两个学科，而且两个学科之间的维数必须相等。在实际应用中，学科往往是3个以上的，并且学科之间维数不一定相等，对此本文提出了一种新型的动态松弛因子法。

在COA中，系统级优化可描述为

在松弛算法中，引入松弛因子ζ，使系统级优化中的等式约束变为不等式约束，扩大搜索区间。

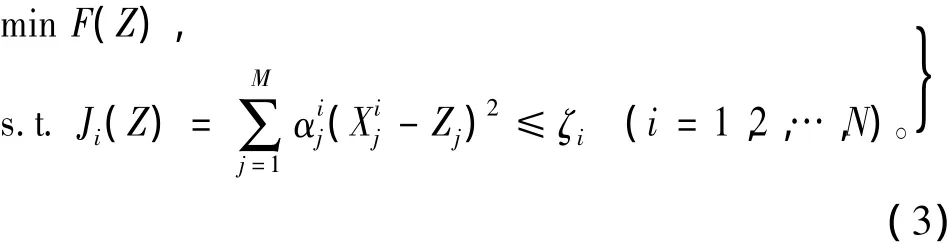
传统松弛算法中，各个约束条件的松弛因子ζi取值相等，这在各约束条件自变量维数相等的情况下是合理的，而对于不同维数的学科取相同的松弛因子，会导致各学科间优化的不平衡。COA是解决自变量松散耦合的优化算法，各约束条件下的自变量维数一般不会相等，因此需要根据自变量的维数来分配松弛因子，在本文所提出的改进算法中，ζi是维数与离散程度的函数。

系统级的搜索空间为如下约束条件的解集。

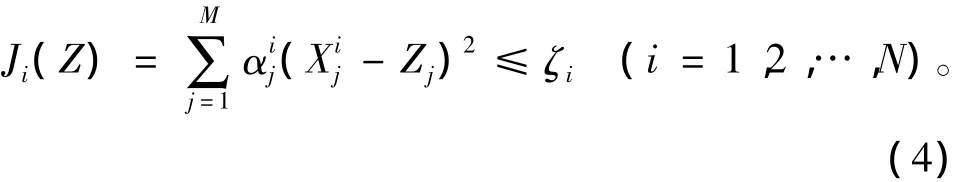
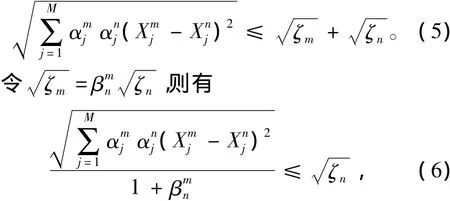
由式（6）可知，第i个学科松弛因子的均方根必须满足

该结果与文献［19］相同，故本文所提出的方法是文献［19］方法的推广，通用性更强。

大量的理论研究及工程实践表明，COA本身是收敛的，但在系统或学科级无法得到最优解时，COA也可能发散。因此，选用合适的系统和学科级优化算法对保证COA的收敛性有很大作用。本文采用粒子群算法，它具有计算简单、收敛速度快、鲁棒性强等优点。任何一种算法在大量的计算中都只能以一定概率获得最优解，为了保证算法的收敛性，本文引入了最优保留策略，即如果本代的优化结果不比上代更优，则用上代结果替换本代。另外，当最优解处于约束条件的边界时，由于一致性约束，有可能出现学科级优化结果满足约束条件，而系统级不满足。为了避免这种情况，本文在系统级优化中将所有的约束条件作为罚函数。图2所示为本文所提出的改进型粒子群COA的流程图。

为了验证改进型COA的优化能力，本文利用经典优化问题——压力容器优化设计对算法进行了测试。图3所示为用于存放压缩气体的压力容器，它由位于两头的锻压半球帽和中间的轧钢圆筒组成，各部件通过焊接连成一个整体。

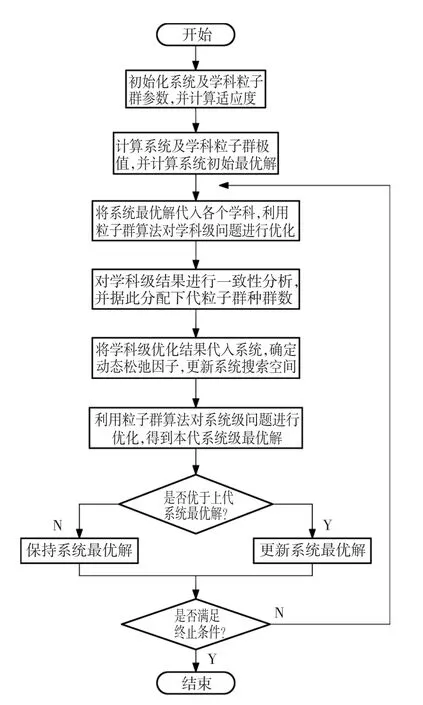
图2 改进型粒子群协同优化算法流程图Fig.2Flowchart of improved particle swarm COA

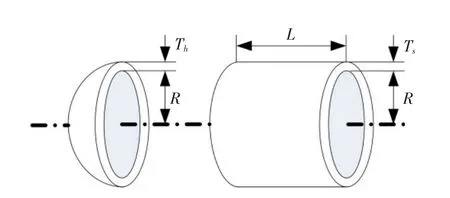
图3 压力容器示意图Fig.3Schematic diagram of pressure vessel

以制造成本最小为优化目标，制造成本包括材料、锻造和焊接成本，优化变量为半球帽厚度Th、圆筒厚度Ts、圆筒内半径R和圆筒长度L，而约束条件则遵照美国机械工程师学会（ASME）制定的锅炉和压力标准设置。该优化问题的数学描述为

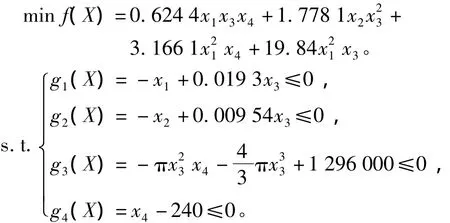
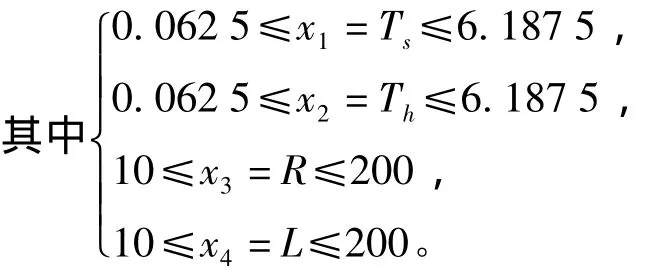
需要指出的是，由于压力容器各部件均由厚度为0.062 5的钢材叠压而成，所以Th和Ts都必须是0.062 5的倍数。

本文在求解该问题时以式（9）作为目标函数

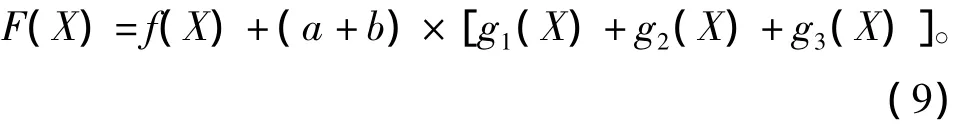
其中，系数a、b的值分别取决于是否满足动态松弛因子要求以及优化问题本身的约束条件，如果满足则取0，反之取一个大的正实数，以达到惩罚的目的。

图4给出了优化过程中目标函数值以及各优化变量的变化曲线，可见改进型COA的收敛速度快且稳定，通过优化使得压力容器的制造成本降低至6 071.8，此时x1=0.812 5，x2=0.437 5，x3=42.098 4，x4=176.637 2。图5给出了采用传统COA的优化结果，其成本为6 112。对比可见，改进型COA在收敛速度、稳定性和优化结果质量方面均要优于传统COA，从而验证了本文所提出改进方法的有效性。

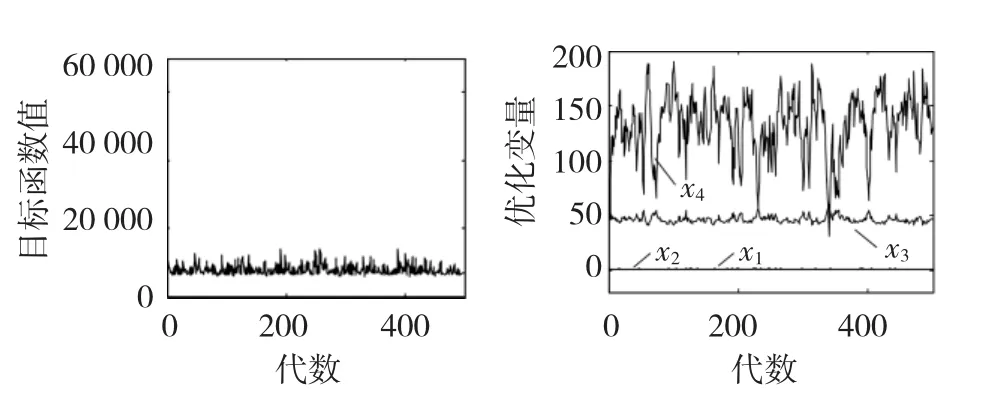
图5 传统COA压力容器设计结果Fig.5Design results of pressure vessel with traditional COA

文献［21］给出了采用粒子群算法（PSO）、高斯粒子群算法（GPSO）、粒子群－文化算法（PSOCA）以及高斯粒子群－文化算法（GPSO－CA）4种方法对同一压力容器优化设计问题的求解结果，分别为8 329.490 8、7 781.111 0、6 201.473 7以及6 112.561 9，本文所提出的改进型COA所得制造成本比这4种方法都要低，从而进一步证明了其性能优势。

2 SRM初始设计及优化

本文首先对一个3相6/4极SRM进行了初始设计，指标如下:电压Vs=270 VDC，额定转速n= 27 000 r/min，额定功率PN=30 kW，额定效率η= 80%。在设计之前，图6给出了主要尺寸的几何意义。

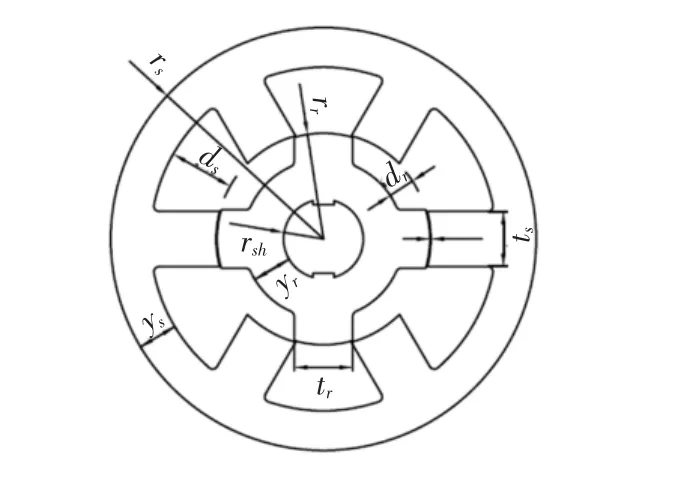
图6 SRM各主要尺寸示意图Fig.6Schematic diagram of the major dimensions in SRM

本文的初始设计主要基于SRM的输出方程［22］，如式（10）所示。

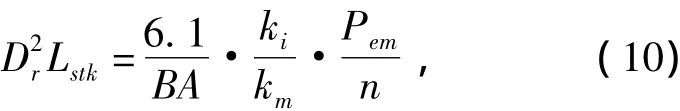
其中:Dr为转子外径;Lstk为铁心叠长;B为磁负荷，此处取0.4 T;A为电负荷，此处取28 000 A/m;ki、km为电流系数，此处取ki=0.5、km=0.8;Pem为电磁功率，其估算式为

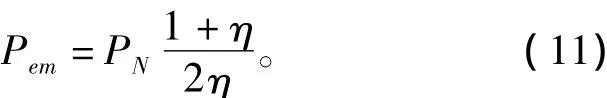
本文采用角度位置法（APC）对SRM进行控制，其中开通角θon和关断角θoff的取值计算为

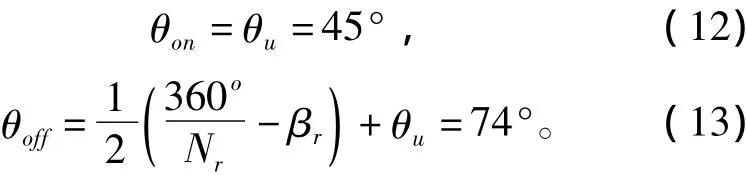
其中:θu为非对齐角位置，记为45°;Nr为转子极数; βr为转子极弧。

本文利用自行开发的SRM性能计算软件对初始方案进行了核算，该软件首先通过等效磁路法和磁共能法获得SRM在某些特定转子位置下的电磁特性，继而利用分段解析法对特性进行表示，最后调用Matlab仿真模型得到电机效率、转矩脉动等性能指标。该软件已经过反复测试，其计算误差在工程允许范围之内。经过核算，在额定转速下，初始设计方案的输出转矩为9.3 N·m，输出功率为26 kW，效率为81.4%，转矩脉动系数为1.344 6。可见，初始方案的性能基本满足指标要求，不足在于输出功率稍低，效率偏低，且转矩脉动系数较大。

SRM的尺寸参数众多，且与电机性能的关系较为复杂，有必要分析它们对电机效率、转矩脉动等的影响模式，进而为优化提供理论依据。在电机外形尺寸不变的前提下，经过理论分析及大量仿真发现下列尺寸对电机的效率具有较大影响:定子轭高ys，转子外径rr，定子极弧βs和转子极弧βr。另外，βs和βr的取值还会影响转矩脉动。

基于上述研究结果，本文从提高效率、减小转矩脉动的角度出发，对SRM的关键尺寸及控制参数进行优化，优化前提是电机外形尺寸Ds和Lstk不变，并引入如下约束条件:对于给定功率与转速的电机，电负荷A与磁负荷B越高，则电机的主要尺寸越小，材料越省，但损耗及温升越高。综合考虑电机的工况以及散热条件，一般可以选取15 000 A/m≤A≤50 000 A/m，0.3 T≤B≤0.6 T。定子绕组的电流密度J主要用于限制电机的铜耗和温升，考虑到SRM的双凸极结构以及定子集中式绕组，其电流密度可以取的高一些，本文取J≤10 A/mm2。定子极最大磁密Bps越大电机铁耗越大，综合考虑所选电机材料的磁化特性曲线与电机损耗，本文取Bps≤1.8 T。需要说明的是，由于本文旨在设计一个高功率密度电机，所以约束条件的上限值均较大。

为了在优化时兼顾电机效率和转矩脉动，将目标函数设为

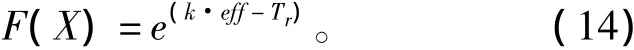
其中:eff为效率;Tr为转矩脉动系数;k的取值可根据优化指标要求以及eff和Tr的范围确定。

1）几何尺寸优化

根据约束条件，将问题划分为两个学科，学科1只包含βs和βr2个优化变量，而学科2则包含rr、rs1、βs和βr四个优化变量，其中rs1=rs－ys为定子内径。图7给出了几何尺寸优化的算法框架。

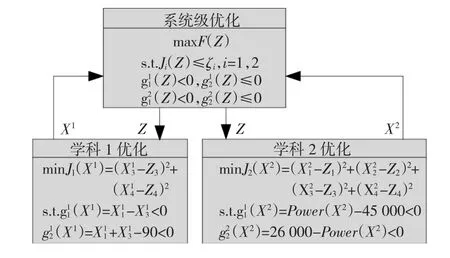
图7 几何尺寸优化算法框架Fig.7Framework of algorithm for dimensions optimization

图8给出了几何尺寸多目标优化的结果，可见优化后的目标函数值为24.82，此时的电机效率为87.7%，转矩脉动系数为1.17，功率为32.6 kW。与初始设计相比，本次优化在一定程度上提高了电机效率，减小了转矩脉动，但效果不是特别明显，主要原因在于在外形尺寸及电、磁负荷等的约束下，只对几何尺寸进行优化，性能的上升空间有限。

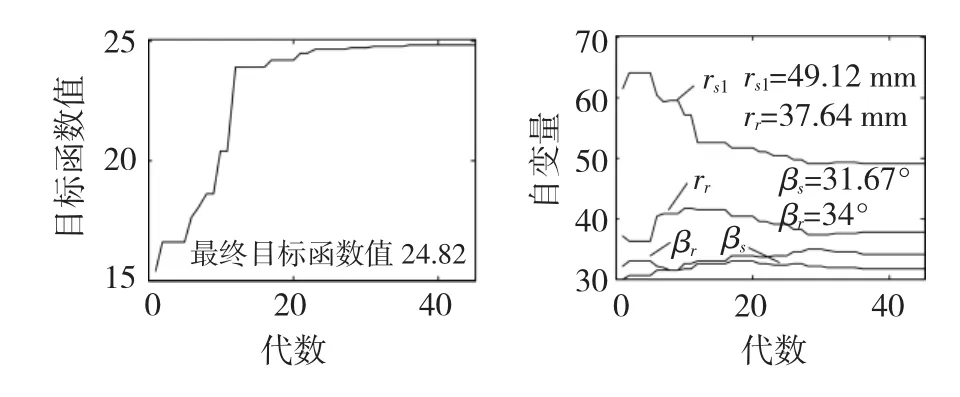
图8 几何尺寸优化结果Fig.8Optimization results of dimensions

2）几何尺寸及控制参数综合优化

众所周知，开关磁阻电机的性能同时受到几何尺寸和控制参数的影响，为了得到系统级的最佳设计方案，应该同时对两者进行优化。在综合优化中仍分为2个学科，与几何尺寸优化不同之处在于学科2增加了2个优化变量，开通角θon以及关断角θoff。

图9给出了综合优化的结果，优化后的目标函数值为3741.9，此时电机效率为89.15%，转矩脉动系数为0.688，功率为31.3 kW。可见，综合优化可以得到比几何尺寸单一优化性能更好的设计方案，效率进一步提高的同时，较大地减小了转矩脉动。综合优化结果即作为本文电磁优化设计的最终方案。需要说明的是，在实际加工时还需根据公差对部分尺寸进行微调，但不会影响电机性能。

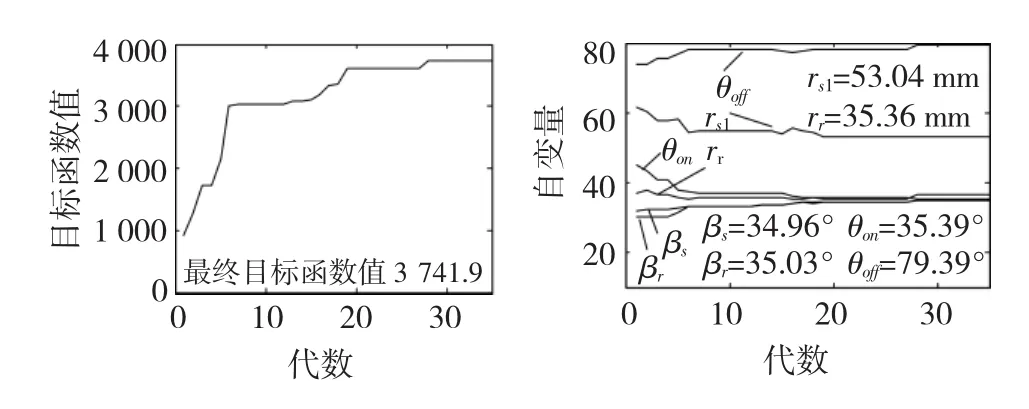
图9 几何尺寸及控制参数综合优化结果Fig.9Optimization results of dimensions and control parameters

3 冷却系统设计

虽然上述综合优化设计方案的性能较初始设计方案有较大提升，但由于其功率密度及热负荷较高，若无冷却系统则难以工程实现。根据电机的损耗及绕组温升情况，本文设计了一个定、转子双水冷系统，并通过集中参数热网络法对增加冷却系统后电机各主要部位的温度进行了核算。图10给出了带有冷却系统的SRM截面图，图中阴影部分为所设计水冷系统的水槽。为了降低水冷系统对电机电磁特性的影响，定子水槽位于电机定子外围的铝壳内，半径r1=6 mm，数量为n=20，并且两两构成一个冷却回路。转子冷却系统的水槽则直接开在电机轴的中心，为了兼顾轴的刚性，半径r2=4 mm，水的流速为1 m/s。

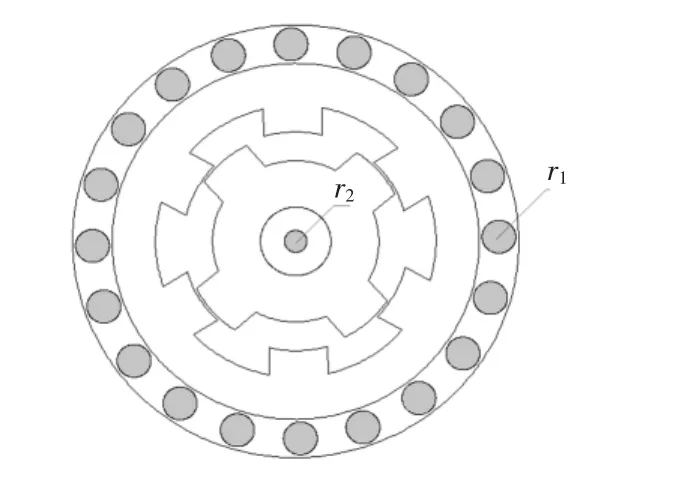
图10 带冷却系统SRM截面图Fig.10Cross-sectional view of SRM with cooling system

图11所示为带冷却系统SRM的集中参数热网络模型，图中热阻R1～R45的计算方法可参见文献［2］，由该模型计算得到的电机各主要部位的温度如下:定子齿127℃，定子轭104℃，转子齿126℃，转子轭110℃，绕组115℃。由此可见，增加定、转子双水冷系统之后，SRM各部位的温度均在工程允许范围之内，且此时冷却水的温度低于80℃。需要说明的是，额定工况下，所设计SRM内的铁耗远大于铜耗，且定子水冷系统对绕组散热效果较好，因而定转子齿的温度要稍高于绕组温度。另外，由于采用了转子水冷，在应用中必须采取一定的动密封措施。

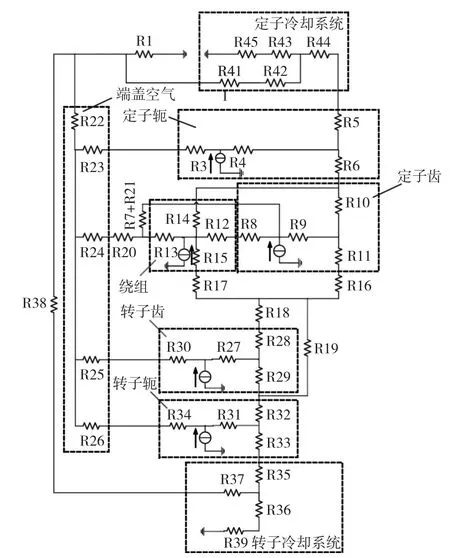
图11 带冷却系统SRM等效热网络模型Fig.11Equivalent thermal network model of SRMwith cooling system

4 结论

本文针对SRM自身特点以及设计中存在的问题，引入COA对一个3相6/4极SRM进行了优化设计和控制。提出了一种新型动态松弛因子法以及最优保留策略，提高了COA的收敛速度、稳定性及优化质量，并通过压力容器优化设计问题对改进型COA的有效性和性能优势进行了验证。在一定的性能要求及约束下，利用改进型COA对SRM的初始设计方案进行了优化，提高效率的同时，较大的减小了转矩脉动。针对优化方案热负荷及温升较高等问题，设计了一个定、转子双水冷系统，使电机各主要部位的温升在工程允许范围之内。本文的工作可以为SRM优化设计及控制，尤其是整个SRM驱动系统的多学科、系统级优化设计提供参考。

［1］VIJAYAKUMAR K，KARTHIKEYAN R，PARAMASIVAM S，et al.Switched reluctance motor modelling，design，simulation，and analysis:a comprehensive review［J］.IEEE Transactions on Magnetics，2008，44（12）:4605－4617.

［2］SONG Shoujun.Detailed Design of a 30 kW Switched Reluctance Starter/Generator System Used in More/All Electric Aircraft［M］.Germany:Shaker Press，2009:28－43.

［3］ZHU Z Q，CHAN C C.Electrical machine topologies and technologies for electric，hybrid，and fuel cell vehicles［C］//Proceedings of IEEE Vehicle Power and Propulsion Conference，September 3－5，2008，Harbin，China.2008:1－6.

［4］CARDENAS R，PENA R，PEREZ M，et al.Control of a switched reluctance generator for variable-speed wind energy applications［J］.IEEE Transactions on Energy Conversion，2005，20（4）: 781－791.

［5］于林科，郑建明.开关磁阻电机直驱电液位置伺服系统模糊滑模控制仿真［J］.哈尔滨理工大学学报，2011，16（5）:76－80.

YU Linke，ZHENG Jianming.Simulation study on fuzzy sliding mode control for switched reluctance motor direct drive electro-hydraulic position servo system［J］.Journal of Harbin University of Science and Technology，2011，16（5）:76－80.

［6］张珍，韦忠朝.开关磁阻电机在家用食物料理机中的应用［J］.湖北工业大学学报，2012，27（1）:84－88.

ZHANG Zhen，WEI Zhongchao.Application of switched reluctance motor to food blender［J］.Journal of Hubei University of Technology，2012，27（1）:84－88.

［7］高洁，孙鹤旭，米彦青，等.计及互感的开关磁阻电机单双相励磁静态性能分析［J］.电机与控制学报，2012，16（11）:45－51.

GAO Jie，SUN Hexu，MI Yanqing，et al.Static performance analysis of SR motor with single and double phase excitation considering mutual inductance［J］.Electric Machines and Control，2012，16（11）:45－51.

［8］张磊，刘闯，王云林，等.开关磁阻电机磁链特性检测与位置信号估计［J］.电机与控制学报，2013，17（2）:28－33.

ZHANG Lei，LIU Chuang，WANG Yunlin，et al.Flux linkage characteristic detection of switched reluctance motor and the position estimate［J］.Electric Machines and Control，2013，17（2）: 28－33.

［9］SOZER Y，TORREY D A.Optimal turn-off angle control in the face of automatic turn-on angle control for switched-reluctance motors［J］.IET Electric Power Applications，2007，1（3）:395－401.

［10］LI Weili，SHENG Man，HUO Fei.Optimal design and finite element analysis of switched reluctance motor for electric vehicles［C］//Proceedings of IEEE Vehicle Power and Propulsion Conference，September 3－5，2008，Harbin，China.2008:1－5.

［11］WU WEI，DUNLOP J B，COLLOCOTT S J，et al.Design optimization of a switched reluctance motor by electromagnetic and thermal finite-element analysis［J］.IEEE Transactions on Magnetics，2003，39（5）:3334－3336.

［12］OWATCHAIPHONG S，CARSTENSEN C，DE DONCKER R W.Optimization of predesign of switched reluctance machines cross section using genetic algorithms［C］//Proceedings of 7th International Conference on Power Electronics and Drive Systems，November 27－30，2007，Bangkok，Thailand.2007: 707－711.

［13］张艳丽，夏斌，谢德馨，等.基于克里金插值技术的开关磁阻电机极面优化设计［J］.电机与控制学报，2013，17（3）: 56－61.

ZHANG Yanli，XIA Bin，XIE Dexin，et al.Optimum design of pole face of switched reluctance motor based on Kriging interpolation［J］.Electric Machines and Control，2013，17（3）:56－61.

［14］RAMINOSOA T，BLUNIER B，FODOREAN D，et al.Design and optimization of a switched reluctance motor driving a compressor for a PEM fuel-cell system for automotive applications［J］.IEEE Transactions on Industrial Electronics，2010，57 （9）:2988－2997.

［15］吴蓓蓓，黄海，吴文瑞.带子星航天器总体参数多学科设计优化［J］.航空学报，2011，32（4）:628－635.

WU Beibei，HUANG Hai，WU Wenrui.Multidisciplinary design optimization of main parameters of spacecraft with sub-vehicles［J］.Acta Aeronautica et Astronautica Sinica，2011，32（4）: 628－635.

［16］SHUAI Zhikang，LUO An，SHEN Z J，et al.A dynamic hybrid var compensator and a two－level collaborative optimization compensation method［J］.IEEE Transactions on Power Electronics，2009，24（9）:2091－2100.

［17］刘涛，梁春华.一种求解生产－配送问题的协同优化方法［J］.哈尔滨理工大学学报，2013，18（1）:120－124.

LIU Tao，LIANG Chunhua.A collaborative optimization approach for production-distribution problem［J］.Journal of Harbin University of Science and Technology，2013，18（1）:120－124.

［18］BOGLIETTI A，CAVAGNINO A，LAZZARI M，et al.A simplified thermal model for variable-speed self-cooled industry induction motor［J］.IEEE Transactions on Industry Application，2003，39（4）:945－952.

［19］李响.多学科设计优化在飞行器设计中的应用［D］.西安:西北工业大学，2004.

［20］温庆国，宋保维，王鹏.基于iSIGHT软件的协同优化算法若干问题研究［J］.西北工业大学学报，2013，31（1）:145－149.

WEN Qingguo，SONG Baowei，WANG Peng.Some problems of collaborative optimization based on iSIGHT［J］.Journal of Northwestern Polytechnical University，2013，31（1）:145－149.

［21］DOS SANTOS COELHO L，MARIANI V C.An efficient particle swarm optimization approach based on cultural algorithm applied to mechanical design［C］//Proceedings of IEEE Congress on Evolutionary Computation，July 16－21，2006，Vancouver，Canada.2006:1099－1104.

［22］吴建华，开关磁阻电机设计与应用［M］.北京:机械工业出版社，2000:110－144.

（编辑:张诗阁）

Multi-objective collaborative optimal design of switched reluctance machine

SONG Shou-jun，GE Le-fei，ZHANG Man
（School of Automation，Northwestern Polytechnical University，Xi’an 710072，China）

Switched reluctance machine（SRM）has multi－variable，strong coupling and highly nonlinear characteristics，and it’s not easy to find optimal design scheme quickly and accurately by traditional methods.To solve this problem，multi-objective collaborative optimal design method was introduced.Collaborative optimization algorithm was improved，and novel dynamic relaxation factor method and elitist strategy were proposed to enhance the convergence speed and accuracy of the algorithm with guarantee of its convergence.Improved collaborative optimization algorithm was used to optimize the efficiency and torque ripple of the initial design scheme of SRM，and the global optimum values of key geometric dimensions and control parameters were obtained.According to the high power density and thermal load of the optimal scheme，a stator and rotor dual water cooling system was designed.By using lumped parameter thermal network model，the temperatures of some important parts of SRM were verified to be acceptable for practical applications.The results of analysis show that application of improved collaborative optimization algorithm can increase the efficiency of the machine and decrease its torque ripple simultaneously.

reluctance motors;multi-objective optimization;collaborative optimization algorithm;dynamic relaxation method;elitist strategy;water cooling systems;thermal network model

10.15938/j.emc.2015.01.010

TM 352

A

1007－449X（2015）01－0068－08

2013－09－06

国家自然科学基金（51107100）;教育部博士点基金（20116102120033）;陕西省自然科学基金（2011GQ7001）

宋受俊（1981—），男，博士，副教授，硕士生导师，研究方向为电机及其系统;

葛乐飞（1992—），男，硕士研究生，研究方向为开关磁阻电机优化设计;

张蔓（1989—），女，硕士研究生，研究方向为开关磁阻电机性能计算。

宋受俊