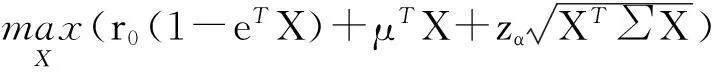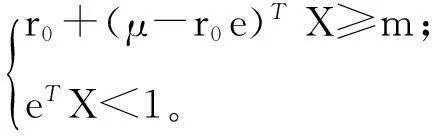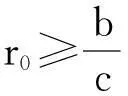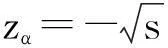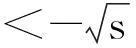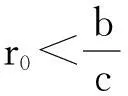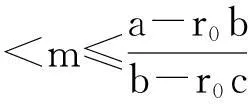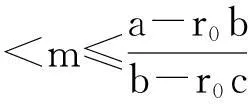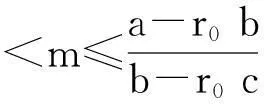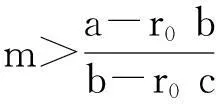考虑无风险资产的安全首要有效投资组合

刘慧宏,丁元耀

(宁波大学,浙江 宁波 315211)



考虑无风险资产的安全首要有效投资组合

刘慧宏,丁元耀

(宁波大学,浙江 宁波 315211)

摘要：安全首要准则在应用于投资策略选择时,更强调投资要预防极端或重大损失的发生。目前三种经典的安全首要投资组合模型皆存在局限性。综合并改进三种经典安全首要投资组合选择模型,以此为基础,建立一个新的考虑无风险资产的安全首要投资组合选择模型,并讨论其最优投资组合策略,该模型更加适合进行国家社会保障基金的投资管理。在存在无风险资产的情形下得到安全首要最优投资组合策略存在的充分必要条件,给出有效投资组合策略的显式表达。

关键词：安全首要准则;投资策略;无风险资产;社保基金投资

一、引言

现代投资组合理论及其应用的既有研究中,除均值—方差准则模型以外,另一类最典型的投资组合选择模型就是安全首要准则模型。经典的安全首要准则模型有三种基本形式,分别是由Roy提出的RSF模型、由Telser提出的TSF模型和由Kataoka提出的KSF模型。早期的研究主要集中于均值—方差模型的理论框架,但是,自1997年亚洲金融危机以来,安全首要准则模型便受到了更多的关注。在理论研究中,RSF模型在连续时间条件下动态化,*Chiu M, Wong H, Li D, “Roy’s Safety-First Portfolio Principle in Financial Risk Management of Disastrous Events，”Risk Analysis, vol.32, no.11(2012.11), pp.1856-1872.TSF模型通过分解可行解集转化为双层最优化问题讨论求解方法,*郑珍:《Telser的安全第一准则下的最优CRP组合投资策略》,硕士学位论文,兰州大学,2012年,第11页。KSF在椭球分布下得到最优解解析式及其存在条件,*Ding Y， Zhang B,“Optimal portfolio of safety-first models,” Journal of Statistical Planning and Inference, vol.139，no.9(2009.09), pp.2952-2962．安全首要准则也与均值—方差准则结合起来研究,用几何方法解释了安全首要准则、期望效用准则及均值方差准则之间的关系,*Li Z, Yao J, Li D,“Behavior patterns of investment strategies under Roy’s safety-first principle,” The Quarterly Review of Economics and Finance, vol.50, no.2(2012.05), pp.167-179.安全首要准则与均值—下半方差准则相结合建立模型。*Promislow D, Young V, “Minimizing the probability of ruin when claims follow Brownian motion with drift,” North American Actuarial Journal, vol.9,no.3(2005.03), pp.109-128．改进型安全首要准则模型对保险资金投资进行风险管理,*陈雷:《基于改进型安全第一准则的保险资金投资风险管理研究》,硕士学位论文,西南财经大学,2012年,第54页。随机可持续回报被引入安全首要准则模型,以研究社会责任投资。*Dorfleitner G, Utz S, “Safety first portfolio choice based on financial and sustainability returns,” European Journal of Operational Research, vol. 221,no.1(2012.08),pp.155-164.无论是理论研究还是应用研究,均取得了比较丰富的研究成果。

不同于均值—方差准则,在安全首要准则下,风险被认为是造成损失或未达到预期的最大可能原因,以潜在的损失概率来测度,投资者在进行投资决策时应优先控制未来收益低于某一水平的概率。安全首要准则在应用于投资策略选择时,更强调投资要预防极端或重大损失的发生。然而,三种经典的安全首要投资组合模型也存在局限性。第一,在RSF模型与TSF模型中,安全收益水平事先已知, RSF模型的目标为破产概率最小,TSF模型的目标是破产概率约束下的期望收益最大。第二,在KSF模型中,安全收益水平事先未知,其目标则是破产概率约束下的安全收益水平最大。现实中,追求收益是几乎一切投资的基本要求,即使像国家社会保障基金的投资,在强调基金安全的同时也要为了实现基金的保值增值而选择收益更高的投资策略。

本文将在综合与改进三种经典安全首要投资组合选择模型的基础上,建立一个新的考虑无风险资产的安全首要投资组合选择模型,并讨论其最优投资组合策略。本文的结构安排如下:第二部分,建立一个考虑无风险资产的双目标安全首要投资组合选择模型;第三部分,根据市场信息对模型进行简化;第四部分,给出模型的最优解及有效前沿;第五部分,考虑不允许筹借资金投资风险资产时,模型的最优解及其存在条件;第六部分进行总结。

二、改进的安全首要投资组合选择模型

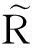
假设Rmin表示投资者所希望的最低安全收益水平,其大小取决于投资者对风险的承受水平α,其中0<α<1。对于投资者而言,以下的模型可以更好地描述其投资决策的行为:

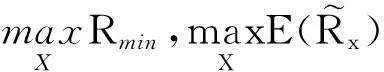
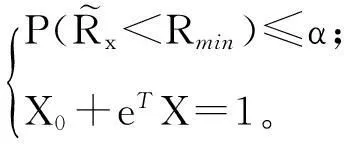
(1)

这是一个双目标安全首要投资组合选择模型。显然模型(1)是对经典安全首要模型的改进,本文称其为改进安全首要投资组合选择模型(ModifiedSafety-FirstModel,简称MSF模型)。

三、简化的改进安全首要投资组合选择模型

为了获得MSF模型(1)的有效投资组合,本文考虑从以下几个方面将模型(1)转变为单目标随机优化模型。

首先,假设投资者想寻找期望收益水平不低于给定水平m的有效投资组合,则MSF模型(1)可以等价为如下模型:

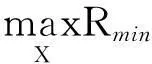
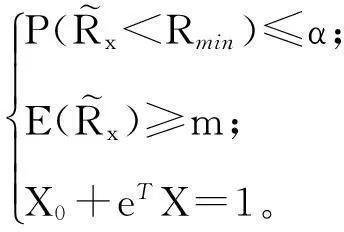
(2)

通常要求m>r0,否则将所有资金存入银行会是最优策略,此时投资者将获得固定收益率r0,这也是安全收益。因此本文将假定m>r0。

其次,假设投资者想寻找安全收益水平不低于给定水平r的有效投资组合,则MSF模型(1)可以等价为如下模型:

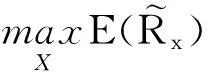
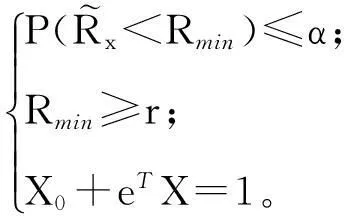
(3)

再次,引入参数λ,则可以将MSF模型(1)等价为如下模型:

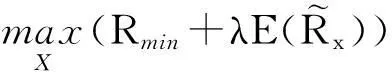
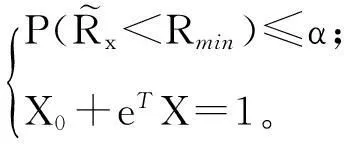
(4)

对于给定的α,如果MSF模型(1)存在有效前沿的话,可以通过求解不同参数值m的模型(2)、不同参数值r的模型(3)或不同参数值λ的模型(4)中的任意一个来获得该有效前沿。因此,本文接下来只讨论模型(2)。

虽然Ding和Zhang曾对模型(2)进行了讨论,但他们只是在不存在无风险资产的情形下讨论了该安全首要模型的最优投资组合策略的选择问题。①Ding Y, Zhang B, “Risky Asset Pricing Based on Safety First Fund Management,”Quantitative Finance, vol. 9,no.3(2009.03), pp.353-361.

(一)风险资产收益服从椭球分布情形

假设收益向量R服从n维椭球分布,即R～En(μ,Ω,gn),密度函数为:

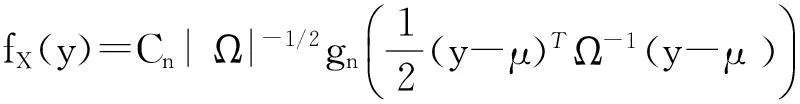
y∈Rn。

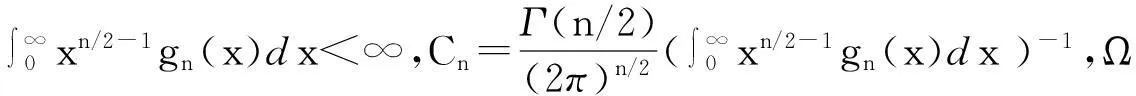
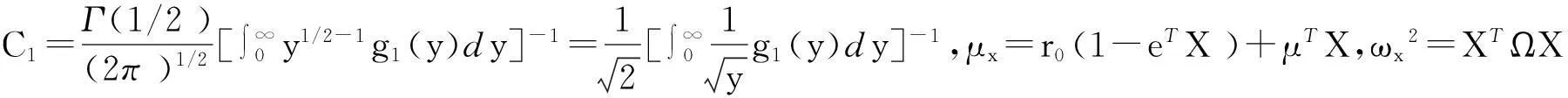
令kα满足:

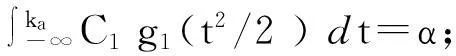
(5)

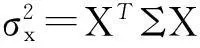
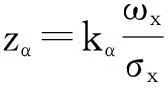
(6)

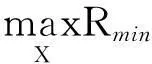
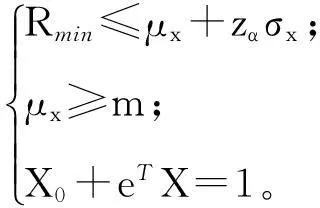
(7)

模型(7)可以进一步表示为:

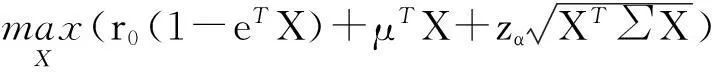
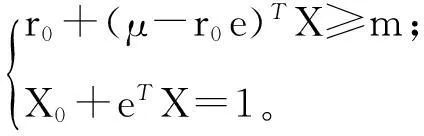
(8)

(二)风险资产收益分布不规则情形

如果收益向量R分布不规则或无法确知其分布类型,那么可以通过著名的Tchebycheff不等式得到:

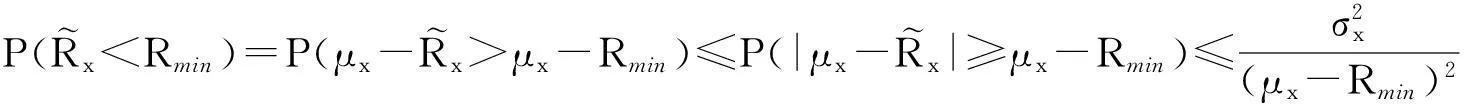
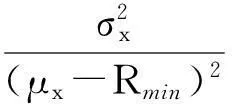
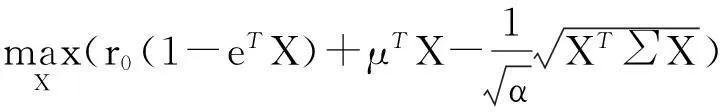
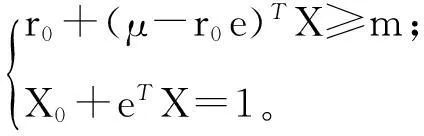
(9)

四、改进安全首要投资组合选择模型的有效前沿

(一)安全首要投资组合最优解及其存在条件

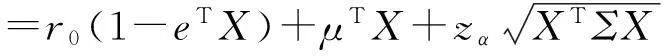
为了表示方便,本文采用如下记号:

a=μT∑-1μ,b=μT∑-1e,c=eT∑-1e,

d=ac-b2,s=a-2br0+cr02。

(10)

容易验证a>0,c>0,d>0,s>0。

根据Kuhn-Tucker条件对凸非线性规划问题——模型(8)进行求解,可以得到定理1。

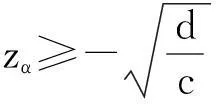
定理1:当m>r0时,安全首要有效投资组合策略存在的充分必要条件是:

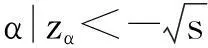
(11)

此时,唯一的安全有效投资组合策略由以下公式给出:

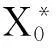
X*=(m-r0)∑-1(μ-r0e)/s。

(12)

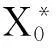
显然,X=0,X0=1对于在任意给定的风险控制水平α下都是一个安全首要有效的投资组合。但是,这个组合对于社保基金的投资应用而言并没有实际价值。

(二)安全首要投资组合的有效前沿及其特征

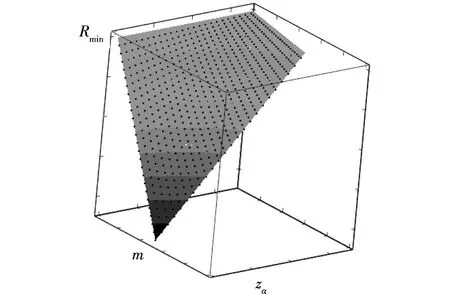
全部安全首要有效投资组合策略的集合构成安全首要投资组合的有效前沿。对于每个有效投资组合策略,对应一个风险控制水平、期望收益水平、安全收益水平的组合(α,m,Rmin);反之,给定满足存在条件的一组(α,m,Rmin),对应一个安全有效投资组合策略。因此,安全首要投资组合策略集也对应于三维空间的一个集合{(α,m,Rmin)},该集合称为MSF投资组合有效前沿。由于风险控制水平α与概率风险度zα一一对应,因此为了更加直观,我们下面用安全首要投资组合策略集对应的集合{(zα,m,Rmin)}描述MSF投资组合有效前沿。对于给定的满足存在条件的风险控制水平α或者概率风险度zα,每个安全首要有效投资组合策略对应一个期望收益水平、安全收益水平的组合(m,Rmin),这些有效投资组合策略的集合或者其对应的二维空间点集{(m,Rmin)},形成α-MSF投资组合有效前沿。MSF投资组合有效前沿与α-MSF投资组合有效前沿统称为安全首要投资组合有效前沿。

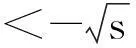
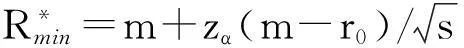
(13)

于是,MSF投资组合有效前沿可以表示为:

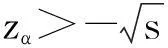
{(α,m,Rmin)|zα<-s,m>r0,

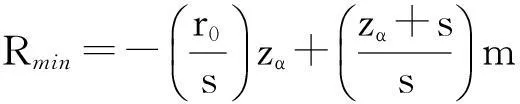
(14)

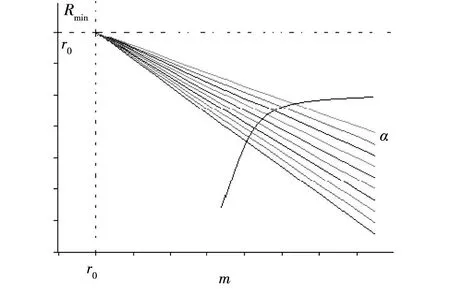
可见,在三维空间α-m-Rmin或者zα-m-Rmin坐标系中,MSF投资组合有效前沿是在范围zαr0,Rmin

图1　MSF安全首要投资组合有效前沿

图2　α-MSF投资组合有效前沿族

总之,安全首要投资组合有效前沿具有如下特征:第一,安全首要投资组合前沿是一个凸开集;第二,任何两个安全首要有效投资组合策略的线性组合仍然是一个安全首要有效的投资组合策略;第三,安全首要有效投资组合策略可以由任何两个有效的安全首要投资组合所生成,即存在两基金分离现象;第四,对于给定的风险控制水平α,安全首要投资组合的均值—方差有效前沿与经典的均值—方差模型有效前沿相同。

五、不允许筹借资金投资风险资产条件下的安全首要投资组合策略

考虑到现实的基金管理中不允许筹借资金投资风险资产,所以显然有约束X0≥0。类似的,模型(8)可以构建不允许筹借资金投资风险资产条件下的安全首要投资组合模型:

(15)

只考虑0<α<0.5情形,此时模型(15)是一个凸非线性规划问题。根据Kuhn-Tucker条件模型(15)进行求解,可以得到定理2与定理3。

安全首要准则不像方差一样局限在资产的波动性上, 还反映了资产损益的分布情况, 是一个更加综合的指标。因此安全首要准则描述风险的思想更加适用于社保基金投资管理。*李仲飞,姚京:《安全第一准则下的动态资产组合选择》,系统工程理论与实践,2004年第1期,第41页。不允许筹借资金投资风险资产的安全首要投资组合策略,与现实的社保基金投资管理要求更加接近,应该能更好地指导社保基金的投资活动,具体将另外撰文讨论。

六、结论

本文的创新之处在于将三种经典形式的安全首要投资组合选择模型集成为一个安全控制条件下的多目标优化模型,并在风险资产收益服从椭球分布和不允许筹借资金投资风险资产的条件下,给出了求解最优投资组合的方法与有效投资组合的显式表达。虽然在相同的经典假设下,安全首要投资组合的均值—方差有效前沿完全相同,但是改进后的安全首要模型,其应用背景和实际意义均有别于均值—方差模型,安全投资者选择投资策略的步骤和操作过程也有别于均值—方差投资者。

另一方面,对于放宽模型假设条件的进一步研究,无论是否具有新的发现,对于理论或者实践都具有一定的意义。

〔责任编辑：沈丹〕

·经济观察·

Security-First Efficient Portfolio of Investment with a Riskless Asset

LIU Hui-hong, DING Yuan-yao

(NingBoUniversity,NingBo315211,China)

Abstract:Security-first principle puts emphasis on prevention from severe loss when it is applied in the selection of investment strategies. Currently the three classical security-first portfolio of investment have limitation. Based on classical security-first portfolio of investment models, the paper put forward an improved security-first portfolio of investment model with a riskless asset which is well adapted to management of investment of social security fund. It obtains the necessary and sufficient conditions for existing optimal security-first portfolios of the model, and then provides explicit expression of efficient portfolio strategies.

Key words:security-first; investment strategy; Riskless Asset; investment of social security fund

作者简介：刘慧宏,男,博士,宁波大学商学院副教授;丁元耀,男,博士,宁波大学商学院教授。

基金项目：国家社科 “社保基金投资的市场风险防控对策研究”(12BGL029);浙江省自然科学 “改进的安全首要投资组合选择理论研究”(LY12G01006)

收稿日期：2014-11-15

中图分类号：F830.5;F832.4

文献标识码：A文章分类号：1674-7089(2015)01-0027-08