改进的Kmeans算法在电厂煤质分析中的应用



潘华1, 高杨杨1, 郑芳1, 刘维明2

(1.上海电力学院 经济与管理学院, 上海200090; 2.镇江谏壁电厂 能源部, 江苏 镇江212006)

摘要:针对传统K-means算法聚类结果受初始值影响、迭代次数多和易出现局部最优解的弊端,研究改变初始值的选择,并采用三角形三边关系定律减少迭代次数对算法作进一步改善.通过数据对比了传统算法与改进算法,结果表明改进算法有较高的准确率.最后,通过实例为电厂的煤种选择提供了参考.

关键词：聚类分析; 数据挖掘; K-means算法; 经济选择

随着经济全球化进程的加快,电力企业所面临的机遇与挑战并存,电力市场也进入了国际化,为了生存和发展,电力企业必须掌握未来资讯.这就意味着企业要充分利用历史数据进行分析、总结,只有掌握企业信息,才能对企业进行管理,保证其良好运行,从而获得最大经济效益.[1]因此,提高电厂经济效益成为每个电力企业所关心的重点.提高经济效益,归根结底是对成本的控制,而如何选择优质煤,降低煤耗,是考虑的主要因素.因为降低发电煤耗可以提升机组的经济运行水平.此外,优质煤还可以降低环境污染,降低因碳排放与硫排放等成分引起的污染治理费用.

目前,聚类分析被广泛应用于农业、医学、电信等领域,聚类初始点的选择、[2]模糊因子的确定[3]等,大部分已经得到解决,但在电力企业的应用还处于初级阶段.随着电力市场竞争的不断扩大,对企业数据进行整理、分析,获取有利信息,也必将成为电力企业的迫切需求.本文结合实际,利用改进的K-means算法,研究聚类算法在A电厂煤经济选择中的应用.

数据挖掘又称为数据库中知识发现(Knowledge Discovery from Database,KDD),是指从大量数据中提取出可信、新颖、有效并能被人理解的模式的高级处理过程.[4]K-means算法属于数据挖掘算法,因为其简单、高效,而且可以用于多种数据类型而被广泛应用.

K-means算法是基于划分的聚类方法,其基本思想是:首先选定K个初始聚类,然后通过迭代的方法,逐次更新各聚类中心的值,直至得到最优的聚类结果.

K-Means聚类基本步骤如下:

步骤1从包含n个对象中任意选出K个对象作为初始簇中心;

步骤2对其中的每一点,计算距离改点最近的中心,并将其分配到该簇,最后形成K个初始分类;

步骤3更新每个簇的中心(即计算每个簇中对象的均值)作为新的中心点,重新计算每个数据到新的中心点的距离,然后再将每个数据和距离其最近的簇分为一组;

步骤4重复步骤2和步骤3,直到分类的重心或均值没有明显变化为止.

1.2　算法的改进

1.2.1聚类中心的选择

在聚类中,欧几里得距离被广泛用于标识两个标量元素的相异度.本文样本点之间的距离采用欧式距离.样本X=(x1,x2,x3,…,xn)和样本Y=(y1,y2,y3,…,yn)之间的距离的计算式为:

d(X,Y)=

(1)

一个样本点X和一个样本集合V之间的距离定义为:

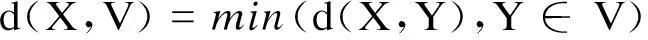
(2)

为了找到在空间分布上相一致的、相似程度较大的数据集合,采取如下步骤:

(1) 找出距离最近的两个点形成一个样本集Q1,并将它们从总样本集P中删除;

(2) 计算Q1中每个样本与P中每个样本之间的距离,找出在P中与Q1中最近的点,将其放入集合Q1中并将其从P中删除;

(3 )直到Q1中的样本个数达到一个阈值;

(4) 再从P中找到样本中数据之间距离最近的两个点构成Q2;

(5) 重复上面的过程直到形成k个点集,最后对k个点集分别进行算术平均,形成k个初始聚类中心.[5]

阈值α的取值因实验数据不同而有所不同.有实验表明,α取0.75时效果较好.[6]

1.2.2减少迭代次数

在K-means算法中,每次计算是将每一个数据对象通过计算均值分到离其最近的簇类中心,对于每个新的分类要重新计算簇类中心,因此当数据较多时,算法耗时较大.本文运用三角形两边之和大于第3边的定律,[4]以减少K-means算法中每次迭代的计算次数,进而缩短计算时间.

令xi∈X,d(cm,cn)为两个聚类中心的距离,那么d(cm,cn),d(xi,cm)与d(xi,cn)3边构成了一个三角形,如图1所示,则d(cm,cn)≤d(xi,cn)+ d(xi,cm),如果d(cm,cn)≥2d(xi,cm),则有d(xi,cm) ≤d(xi,cn),即xi到中心cn的距离比到cm的距离大.因此,在d(cm,cn)≥2d(xi,cm)的前提下,不必计算d(xi,cn).

图1　构成的三角形

2算法和实验对比

2.1　算　法

经过改进后的K-means算法描述如下.

(1) 计算任意两个样本之间的距离d(X,Y),找到集合P中距离最近的两个点形成集合Qm(1≤m≤k),从集合P中删除这两点.

(2) 在P中找到距离集合Qm最近的点将其放入集合Qm,并从集合P中删除该点.

(3) 重复(2)中步骤,直到集合中的样本点个数大于等于αn/k(0<α≤1).

(4) 如果m

(5) 将最终形成的k个集合中的样本点分别进行算术平均,从而形成k个初始簇中心cj(I),j=1,2,3,…,k.

(6) 从这k个初始聚类中心出发,计算每两个聚类中心间的距离d(xi(I),cj(I)),[5]其中i=1,2,3,...,k;j=1,2,3,...,k.

(7) 设xi当前所在的类为Qm,计算xi与Qm类中心的距离d(xi,cm(I)).若d(cm(I),cj(I))≥2d((xi,cm(I))不成立,则计算d(xi,cj(I));若d(xi,cj(I))

(9) 若|Jc(I+1)

2.2　实验对比

为验证此次改进算法的优越性,我们将传统的K-means算法和改进的K-means算法进行了比较,结果如表1所示.表1中的2组实验数据Wine和Iris源于UCI数据库(UniversityofCaliforniaIrvine).

表1　两者算法的实验数据对比

由表1可知,计算得出改进后算法的准确率高于传统的K-means算法,能得到较好的细分效果,可以用于对实际数据的聚类分析.此外,在第一个迭代阶段指定聚类簇时,改进的K-means算法实际上已经减少了计算量.当数据集中的样本点很多时,即n较大时,其优越性将更明显.

3实例分析

本文以A电厂入厂煤的相关数据为研究对象.众所周知,影响煤炭质量的因素很多,例如水分、灰分、挥发份、硫含量、空气干燥基水分等多个因素.在未进行聚类前,数据分布杂乱,很难发现有用的信息,因此需要对原始数据进行预处理.

根据影响因素之间的关系以及因素对煤质量造成的影响程度分析,最终确定了其中10个重要因素为影响煤质量的关键因素.具体如下.

Aar为收到的基灰分;Ad为干燥基灰分,煤燃烧之后留下的残渣部分,灰分越高,说明煤中可燃成分较低、发热量就低;[7]Fcd为固定碳,其含量越多越好;Mtar为水分;Mad为空气干燥基水份,一般说来,水分高会影响煤的质量,在煤的利用中,水分高的煤难以破碎,煤炭中的水分通常要求在10%左右;Std为硫分;Sar为硫元素含量,两者属于煤中的有害元素,通常要求其在1%以下才能用于燃烧,过多的硫分会对设备造成损害;Var为收到的基挥发分;Vd为干燥基挥发份;Vdaf为干燥无灰基挥发分,3者用来判断煤的变质程度,燃烧中也可用来确定锅炉型号和煤炭分类.

根据这10维特征对数据进行了分析比较,如表2所示.然后用改进的K-means算法进行聚类分析,实验结果如表3所示.

表2　根据样本因素处理过的部分电厂煤数据　%

表3　采用改进的K-means算法进行分析后的实验结果　%

由表3可以看出,第2类的灰分明显高于其他两类,且固定碳含量过低.在电厂发电需求中,这类煤的燃烧效率与另外两类相比太低,且在3类煤中,其质量最差.第1类与第3类相比,其灰分含量高于第3类,在燃烧后会产生比第3类更多的废渣;其次,在硫分的对比上,第1类为1%,而第3类只有0.51%.因此,无论是从废渣处理还是从废气排放来看,第3类的煤炭质量都要优于第1类.

因此,从煤炭质量角度考虑,第3类煤炭应作为电厂采购入厂煤时的第一选择.

而从电厂采购煤种统计情况来看,第3类煤中神混煤与伊泰3#煤居多,因此电厂可以考虑主要使用这两个品种.

4结语

针对传统K-means算法聚类结果受初始值影响和耗时长的弊端,将传统算法进行了分析改进.为验算改进后算法的优越性,将改进的K-means算法与传统算法进行了对比.然后,将改进的K-means算法对A电厂的入厂煤数据进行了分析,并对历史数据进行了聚类分析,从历史数据中了解数据信息以求寻找更符合电厂经济效益和生态效益的入厂煤品种,以期为决策者在选择煤种时提供参考.

参考文献：

[1]邢继武.提高电厂经济效益途经浅析[J].经济论丛,2012(16):181.

[2]GONZALEZ T.Clustering to minimize and maximum inter cluster distance [J].Theoretical Computer Science,1985,38(2-3):293-306.

[3]PAL N R.BEZDEK J C.On cluster validity for the fuzzy c-means model [J].IEEE Transactions on Fuzzy Systems,1995,3(3):370-379.

[4]吴昌晟.数据仓库在企业资源计划中的应用研究[D].武汉:华中科技大学,2005.

[5]耿筱媛,张燕平,闫屹.改进的K-means算法在电信客户细分中的应用 [J].计算机技术与发展,2008(18):164-167.

[6]袁方,孟增辉,于戈.对K-means聚类算法的改进[J].计算机工程与应用,2004(36):44-48.

(编辑胡小萍)

(1.School of Economics and Management, Shanghai University of Electric Power, Shanghai200090, China;

2.Department of Energy,Zhenjiang Jianbi Power Plant, Zhenjiang212006, China)

Abstract:In view of the fact that the traditional K-means algorithm for clustering results are affected by the initial value,the number of iterations and the more likely defect of local optimal solution,a study is conducted on the initial value selection and the triangle trilateral relations law is adopted to reduce the number of iterations of the algorithm for further improvement.Through comparison of the traditional algorithm and the improved algorithm,the results show that the improved algorithm has higher accuracy.Finally,an economic choice support in power plant coal is examplified.

Key words:clustering analysis; data mining; K-means algorithm; economic choice

中图分类号：TM621; TK16

文献标志码：A

文章编号：1006-4729(2015)06-0585-04

基金项目：国家自然科学基金(71271065).

通讯作者简介：潘华(1976-),男,副教授,上海人.主要研究方向为电力信息化与决策支持,电力工程施工管理等.E-mail:stevepan2005@126.com.

收稿日期：2015-04-20

DOI：10.3969/j.issn.1006-4729.2015.06.018