弹性力学平面问题的几种解法

明星 沈强

（郑州大学 土木工程学院，河南 郑州 450001）

弹性力学作为固体力学的一个重要分支，它是研究弹性固体由于受外力作用，边界约束或者温度改变及其他一种或多种外界条件作用下产生的应力、应变和位移。它的研究对象是板、壳、实体以及单根杆件。可以说弹性力学是材料力学问题的精确解，是结构力学，塑性力学等力学学科的基础，其广泛应用于土木工程、航空航天工程及机械工程等多个学科领域。并且随着科学技术手段的进步，电子计算机得以应用到弹性力学的计算分析中，这极大地促进了弹性力学问题的分析计算更加深入，促使了有限单元法得以实现。因此本文从弹性力学最基本的平面问题出发，通过求解平面问题的解析法、数值法和试验方法来感受弹性力学研究问题的手段、方法，体会弹性力学的魅力，并为其它力学学科的学习打下基础。

1 解析法

解析法是根据研究对象在结构中的静力平衡条件，几何关系和物理关系建立边界条件，平衡微分方程，几何方程和物理方程，并以此求解应力分量，应变分量和位移分量的一种平面问题的精确解法。按求解时的基本未知量选取不同可分为按位移求解的位移法和按应力求解的应力法。

（1）位移法：以位移为基本未知量时的基本方程如下

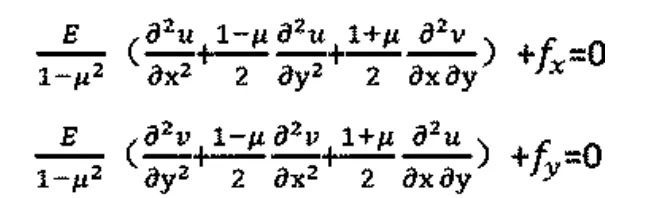
位移边界条件如下

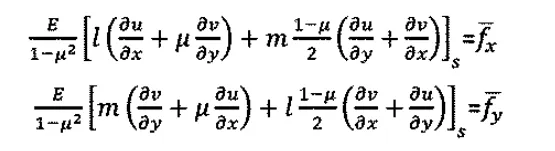
从上面的公式可以看出位移法求解平面问题时的基本未知量只有两个，与应力法的三个基本未知量相比求解简单很多，并且不但能求解位移边界条件，还能求解应力边界条件与混合边界条件。

(2)应力法：应力法以应力分量作为基本未知量，由此平面问题的平衡微分方程，几何方程，物理方程以及边界条件经过推导可变为如下形式：

基本方程：

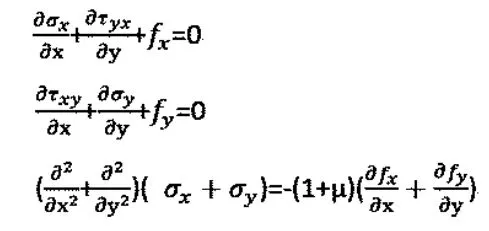
应力边界条件：

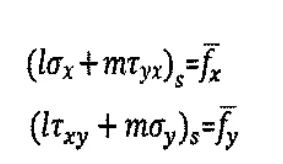
值得注意的是按应力求解时边界条件应全部为应力边界条件。对于位移边界条件，虽然在局部边界上可用圣维南定理转化为应力边界条件，但此时得到的解答已不是精确解，同时上述推导过程是基于平面应力问题的，对于平面应变问题应把弹性常数作相应调整。

2 数值解法

弹性力学平面问题的解法虽然针对某些问题来说可以得到精确解，但是其不适合实际工程中复杂问题的计算。相反的，数值分析方法虽然只是对实际问题的近似解答，但其求解时的过程清晰，步骤明确，便于编程，并且工程上常有安全系数的保证，因此近似解与不会对实际工程造成太大影响。从而使数值分析方法在工程问题中得到大量应用。数值分析方法有以下三种：

差分法：用差分方程替代平衡微分方程，将求解微分方程变为求解代数方程，简化了计算。

变分法：变分法其实是一种能量法，以外力所做的功及弹性体的应变势能来建立弹性力学的求解方程。其中基本未知量为弹性体的虚位移，运用的基本原理为虚位移原理和最小势能原理。

有限单元法：在力学模型上进行近似将弹性体简化为有限个单元体，且各单元体之间仅在有限个结点处交铰结而成的结构物。然后进行单元分析，形成单元刚度矩阵，进行整体分析，集成整体刚度矩阵，并运用矩阵位移法求解。有限单元法便于编程，因此随着电子计算机技术的发展得以广泛应用于工程实践的各个方面。相关软件有ANSYS、ADINA、MSC、ABAQUS。

3 实验的方法

除了解析法和数值分析方法外，工程上常用的简单实用的方法还有实验法。将弹性体贴上应变片，连接上计算机便可以轻松模拟计算弹性体的内力分布情况。

4 结论

弹性力学问题求解的解析法，数值分析方法和实验法各有千秋，应结合具体的工程实际问题选用合适的方法。同时也应认识到目前弹性力学求解方法并不完善，在工程中中仍有许多问题还无法得到令人满意的结果。因此学习掌握弹性力学的现有方法，并结合科学技术的发展和认识了解的加深提出新的，更加符合实际工程要求的弹性力学求解方法才是弹性力学研究的根本目的所在。