无限维系统中的量子纠错定理

王 丽,孙凡果,贺 衎

(太原理工大学 数学学院,太原 030024)

无限维系统中的量子纠错定理

王 丽,孙凡果,贺 衎

(太原理工大学 数学学院,太原 030024)

信息在传输过程中，经常会受到噪声的影响。为了避免噪声的影响，就需要对量子信息进行纠错。 量子纠错定理描述量子信道可纠错的充分必要条件。但目前的纠错定理基于有限维量子系统给出。 本文研究无限维量子纠错定理，给出量子信道具有有限维纠错码的充要条件。

量子信道;量子纠错;编码

在量子力学中,一个量子系统由复希尔伯特空间H表示。一个量子态可以表示成一个迹为1的正算子ρ.用B(H)表示所有有界线性算子的全体,T(H)表示所有迹类算子的全体。迹范数定义为

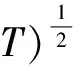
如果ρ2=ρ,则ρ为纯态;如果ρ2≠ρ,则ρ为混合态。用S(H)表示复希尔伯特空间H上所有态的全体。通过量子纠错可以避免在量子信息传输过程中噪声和其它不必要的干扰。量子纠错理论发展成了类似于噪声信道的经典编码[2-4,7-9]并且一些研究人员开发出了优化的量子纠错理论[5-6,10-12]。

量子信道ε:T(H)→T(H)是一个完全正的保迹线性映射。在文献[13]中讨论了无限维系统的量子信道表示量子信道ε的算子和表示为

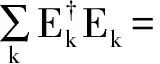
1 主要结论和证明

设C是复希尔伯特空间H的子集, 并且P是H到C上的正交投影, 如果存在一个量子信道R:T(H) →T(H) 使得

R∘ε(ρ)=ρ.

对所有满足ρ=PρP的ρ∈T(H)都成立,则C是信道ε上的一个量子纠错码(QECC)。下面的定理是主要结论。

PEi†EjP=αijP.

式中,D=(αij)∈T(l2)是一个密度算子。

由上述定理,得到下面推论。Mn代表n阶矩阵。

PEi†EjP=αijP.

式中:D=(αij)是一个正矩阵。

为证明定理1,需要下面引理。

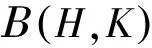
则

1)Φ是正的当且仅当对所有|ψ〉∈Η,存在压缩矩阵Ω=(ωji(|ψ〉))j,i使得

C|ψ〉=Ω(|ψ〉)A|ψ〉 ;

2)Φ是完全正的当且仅当存在压缩矩阵Ω=(ωji)j,i∈Β(l2)使得

C=ΩΑ.

式中：A=(A1,A2,…,An,…)T;C=(C1,C2,…,Cn,…)T;ΩΑ=(ωjiI)A=(Ω⊗I)A.

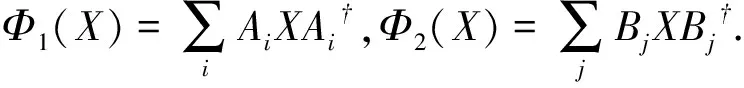
引理2的证明 定义Φ=Φ1-Φ2,Ψ=Φ2-Φ1。显然Φ和Ψ是从T(H)到T(K)的线性映射。 我们知道T(H)的对偶空间是B(H),用Φ*和Ψ*∶B(K)→B(H)分别表示Φ和Ψ的共轭, 则对任意X∈B(K)

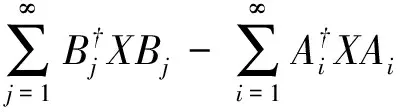
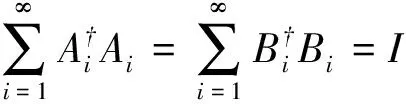
如果Φ1=Φ2, 那么Φ*=0,Ψ*=0, 这说明Φ*和Ψ*是从B(K)到B(H)的完全正的线性映射。 所以存在压缩算子Ω=(ωij)和Γ=(γji)使得Α=ΩΒ,Β=ΓΑ.

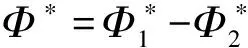
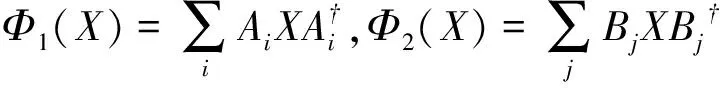
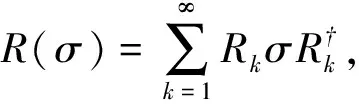
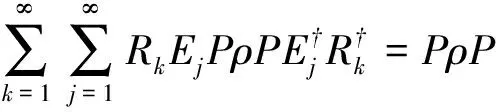
通过引理1,存在复数βkj使得

RkEjP=βkjP

对所有1≤j≤∞,1≤k≤∞都成立。注意

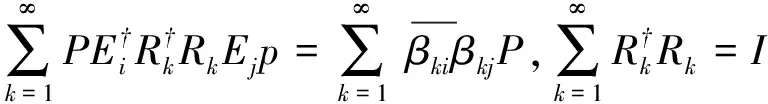
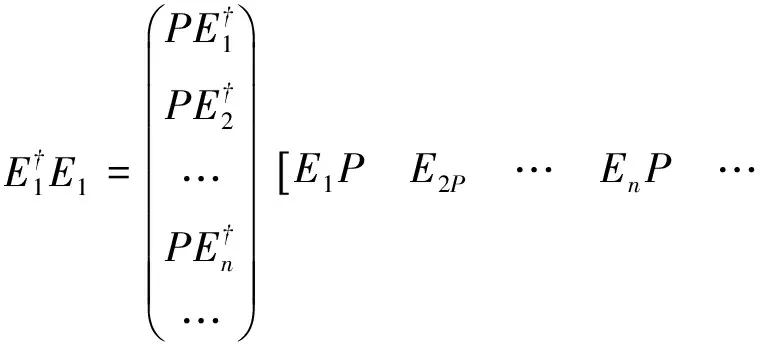
(αijp)=D⊗P.

因此D≥0.

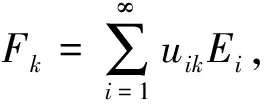
通过替换

由算子的极分解,存在算子Uk使得

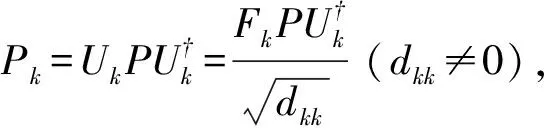
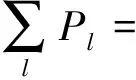
对任意满足ρ=PρP的ρ,

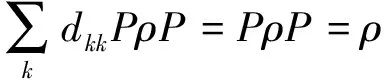
所以,C是ε的量子纠错码。证明完成。

Hou J C.A haracterization of positive linear maps and criteria of entanglement for quantum states.J Phys A:Math Theor，2010，43(38):385201-385220.

Gottesman D.Class of quantum error-correcting codes saturating the quantum Hamming bound.Phys Rev A，1996，54(3):1862-1868.

Steane A M.Error Correcting Codes in Quantum Theory.Phys Rev Lett，1996，77(5):793-797.

Knill E，Laflamme R.Theory of quantum error-correcting codes.Phys Rev A，1997，55(2):900-911.

Kosut R L，Lidar D A.Quantum Error Correction Via Convex Optimization.Quant Ief Proc,2009,443(8):443-459.

Kosut R L,Shabani A，Lidar D A.Robust Quantum Error Correction via Convex Optimization.Phys Rev Lett,2008，100(2):020502-020505.

Nielsen M A，Chuang I L.Quantum Computation and Quantum Information.Cambridge:Cambridge University Press，2000.

Shor P W.Scheme for reducing decoherence in quantum computer memory.Phys Rev A，1995，52(4):2493-2496.

Laflamme R，Miquel C，Paz J P，et al.Perfect Quantum Error Correcting Code.Phys Rev Lett,1996，77(1):198-201.

[10] Reimpell M,Werner R F.Iterative Optimization of Quantum Error Correcting Codes.Phys Rev Lett,2005，94(8):080501-080504.

[11] Soraya Taghavi，Robert L.Kosut，Life Fellow.Daniel A.Lidar，IEEE TRANSACTIONS ON INFORMATION TEORY，2010，56(3):1461-1473.

[12] Yamamoto N，Hara S，Tsumara K.Suboptimal quantum-error-correcting procedure based on semidefinite programming.Phys Rev A，2005，71(2):022322- 022327.

[13] Wang L，Hou J C，Qi X F.Fidelity and entanglement fidelity for infinite-dimensional quantum system.J Phys A,2014，(47):304-335.

(编辑：刘笑达)

Theory of Quantum Error-Correction in Infinite-Dimensional Quantum System

WANG Li ，SUN Fanguo，HE Kan

(CollegeofMathematics，TaiyuanUniversityofTechnology，Taiyuan030024，China)

Information is often affected by noise during transmission. In order to avoid the effect of noise,it is needed to correct the quantum information.The current quantum error-correction theory gives the sufficient and necessary conditions for the error-correction of quantum channel in finite dimensional quantum systems. In this paper,the quantum error-correction theory in infinite dimensional quantum systems was studied,and the necessary and sufficient conditions were given for the error-correction of quantum channel with finite dimensional error correcting codes.

quantum channel;quantum error-correction;infinite dimensional quantum systems

1007-9432(2015)04-0480-03

2015-01-10

国家自然科学基金项目资助：纠缠破坏信道和量子测量的代数结构和几何特征(11201329)

王丽(1980-)，女，山西运城人，博士，主要从事算子代数与量子力学研究，(Tel)15035115553

贺衎，男，副教授，(Tel)13803496971

O177.1

A

10.16355/j.cnki.issn1007-9432tyut.2015.04.024