机械微细加工辅助用超声振动台的设计

赵 蕾,梁 欣,吕 明,王时英,刘建成,2

(1.太原理工大学 机械工程学院,太原 030024;2.美国太平洋大学,美国 加利弗尼亚州 95211)

机械微细加工辅助用超声振动台的设计

赵 蕾1,梁 欣1,吕 明1,王时英1,刘建成1,2

(1.太原理工大学 机械工程学院,太原 030024;2.美国太平洋大学,美国 加利弗尼亚州 95211)

基于一维纵向振动理论,利用理论解析法设计了机械微细加工辅助用振动平台。利用有限元软件进行优化设计,确定了圆锥段的最佳开槽数量和圆柱段的最佳开狭缝数量,改善了工作面的振幅分布均匀性,增大了工作面的振幅；增加圆锥段的长度以减小振动平台的谐振频率,通过有限元分析，研究了振动平台的谐振特性,满足工程应用的要求,验证了设计方法的可行性。为大尺寸振动体的设计提供了一种简便的方法。

超声振动；微细加工;振动平台设计；理论解析法;有限元法;谐振特性

超声机械微细加工是将超声振动与传统机械微细加工相结合的一种新型加工工艺,可以减小切削力、延长刀具寿命、提高工件的加工精度和加工质量[1-3]。

振动平台的设计是超声机械微细加工工艺的关键技术之一,其谐振特性关系到加工质量。由于振动平台的直径大于1/4波长,振动平台不仅做纵向振动,而且还做横向的耦合振动,利用一维纵向振动设计理论的设计误差较大。林玉书等利用耦合振动理论研究了大尺寸塑料焊接工具的三维振动,并研究了横向振动与开槽之间的关系,改善了工具辐射面上的位移分布均匀程度[4];周光平等利用表观弹性法对圆柱体、空心圆柱体、矩形六面体等耦合振动单元进行分析,并利用开槽、开狭缝、增加弹性体和二次设计等方法来控制超声振动体的振动[5],但是上述设计方法较为复杂。

笔者基于一维纵向振动理论,利用理论解析法设计振动平台,用有限元分析法研究了开槽数量和开狭缝数量对振动平台谐振特性的影响,并进一步对振动平台的谐振频率进行优化,使振动平台的谐振特性满足工程应用的要求。

1 振动平台理论分析模型的建立

机械微细加工辅助用超声振动系统，主要由超声波发生器、换能器和振动平台组成。超声波发生器和换能器是比较成熟的器件,有专门的厂家生产；为了整个振动系统谐振，振动平台的频率与换能器一致，这需要进行专门的设计。振动平台的理论分析模型如图1所示,右端面为工作面；d1，d2为振动平台的小端直径和大端直径；l1，l2为振动平台圆锥段长度和圆柱段长度；以左端面的圆心为原点,中心线为x轴,向右为正方向建立坐标轴。

图1 振动平台的理论分析模型Fig.1 Vibration Analytical Model for Ultrasonic Vibration System

2 振动平台的理论设计

忽略振动平台的横向振动,仅考虑沿x方向的轴向振动,振动平台圆锥段的位移函数和应变函数分别为[6]:

(1)

(2)

振动平台圆柱杆段的位移函数和应变函数分别为:

ξ2=a21cos(Kx)+a22sin(Kx) ，

(3)

(4)

振动平台只做一维纵向振动时,在x=l1处圆锥杆与圆柱杆的位移和力相等,即有边界条件:

(5)

(6)

振动平台的左端面与换能器连接,振幅最大,则振幅的导数为零,即:

(7)

振动平台的右端面自由振动,受力为零,即:

(8)

式(5)-(8)是关于a11，a12，a21，a22的齐次方程组,要使待定系数a11，a12，a21，a22不全为零,则方程组系数行列式的值必为零,因此有:

(9)

式中的Dij是式(5)-(8)中a11，a12，a21，a22的系数,式(9)即为振动平台的频率方程。

3 振动平台的设计和有限元分析

振动平台的谐振频率f=20kHz,材料为45钢,密度ρ=7 810kg/m3,弹性模量E=209GPa,小端直径(由换能器的直径确定)d1=56mm,圆柱段的直径(由使用要求决定)d2=100mm。为了减小圆柱段的横向振动,需保证圆柱段的厚径比大于0.3,取圆柱段长度l2=40mm。式(9)中仅圆锥段长度l1未知,利用MATLAB编程计算,计算结果如图2所示,l1=73.03mm。

图2 圆锥段长度l1计算结果Fig.2 Relationship Between Solution Δ and l1

图3 f=22.830 kHz时,振动平台的位移云图Fig.3 Mode shape of Ultrasonic Vibration System

图4 振动平台工作面的相对振幅分布曲线Fig.4 Relationship between displacement and r

根据振动平台的形状参数建立三维模型,导入有限元软件ANSYS12.0,采用Solid95单元进行自由网格划分,模态提取方法为BlockLanczo,搜索频率阶数为15阶,起始搜索频率为15kHz,进行模态分析,分析结果显示在f=22.830kHz时振动平台主要做纵向振动。振动平台的位移云图如图3所示,左端面处的相对振幅最大。工作面的相对振幅分布曲线如图4所示,最大相对振幅为0.549,最小相对振幅0.364,振幅相差较大,需要进一步采取措施,抑制圆柱段的横向振动,改善工作面的振幅分布均匀程度。

为抑制振动平台的横向振动,常用的方法是在振动体上开槽,开槽的宽度为λ/25～λ/20。频率f=20kHz的纵波在45钢中的波长λ=(E/ρ)1/2/f=258.65mm,取在圆锥段上开槽的宽度为10mm,开槽深度为22mm,槽均布于圆锥段。改变开槽的数量,工作面的最小振幅与最大振幅之比α，振动平台的谐振频率f的变化曲线分别如图5、图6所示。

图5 开槽数量对工作面振幅分布均匀程度的影响Fig.5 Relationship between α and the number of solt

图6 开槽数量对振动平台谐振频率f的影响Fig.6 Relationship between frequency and the number of solt

开槽数量n1<12时,随着开槽数量的增加,工作面的最小振幅与最大振幅之比增加；开槽数量n1>12时,随着开槽数量的增加,工作面的最小振幅与最大振幅之比减小,振动平台的谐振频率随着开槽数量的增加而减小。因此，确定圆锥段的开槽数量n1=12,此时振动平台的位移云图和工作面的振幅分布曲线分别如图7、图8所示。振动平台的左端面与YP-7015-4Z型换能器连接,振幅为8μm,由此计算得工作面的最大振幅为3.77μm,输出振幅较小。

图7 开槽数量为n1=12时,振动平台的位移云图Fig.7 Mode Shape of Ultrasonic Vibration System (n1=12)

图8 开槽数量n1=12时,工作面的相对振幅分布曲线Fig.8 Relationship between displacement and r(n1=12)

为了增加工作面的振幅,在圆柱段均匀地开细缝,细缝的宽度为5mm,深度为20mm,长度为20mm,距工作面的距离为10mm。改变细缝的数量,工作面的最大振幅ξ、最小振幅与最大振幅之比α、振动平台的谐振频率f如表1所示。随着细缝数量的增加,工作面的最大振幅ξ随之增大,振动平台的谐振频率f随之增加。由表1可以确定狭缝的数量为20。

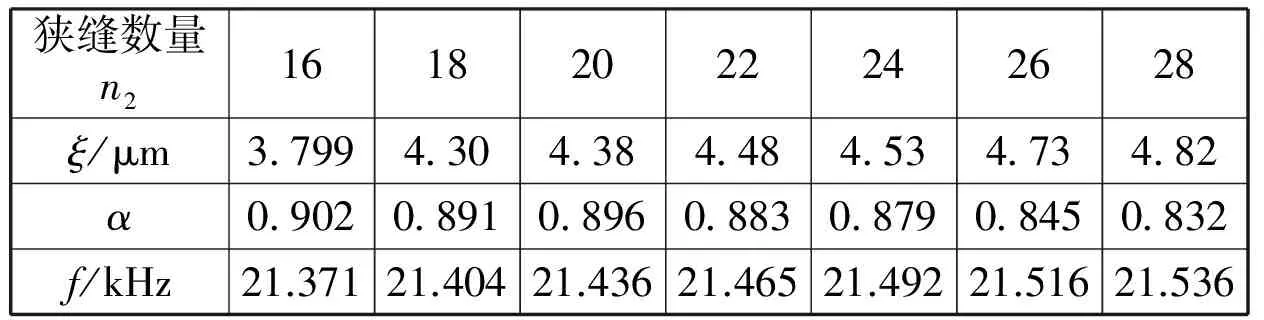
表1 狭缝数量对振动平台谐振特性的影响

为减小振动平台的谐振频率,增加圆锥段的长度l1,当l1=83mm时,振动平台的谐振频率f=19.890kHz,位移云图如图9所示,工作面的相对振幅分布曲线如图10所示。从图中得知，工作面的最大振幅为4.37μm,最小振幅与最大振幅之比α=0.916,谐振特性满足工程应用的要求。

图9 振动平台的位移云图Fig.9 Mode Shape of Ultrasonic Vibration System

图10 振动平台的相对振幅分布曲线Fig.10 Relationship between displacement and r

4 结论

1) 基于一维纵向振动理论,利用理论解析法设计了大尺寸振动体,并利用有限元分析进行优化设计,使其谐振特性满足工程应用的要求,为大尺寸振动体的设计提供了一种简单的方法;

2) 随着圆锥段开槽数量的增加,振动平台工作面的最小振幅与最大振幅之比α增大,开槽数量为12时,α最大,改善了工作面振幅分布的均匀性;

3) 随着圆柱段开狭缝数量的增加,工作面的最大振幅随之增大,振幅分布的均匀性变差,经综合考虑确定最佳狭缝数量n2=20;

4) 可以通过增加振动体的长度来减小谐振频率,使振动平台与振动系统的其余器件实现谐振。

[1]LEESK,JANGSH,LEESW,etal.Geometricmachiningmechanismoftheultrasonicdrilling[M].Switzerland:TransTechPublicationsLtd,2007:66-71.

[2]ThomasPNH,BabitskyVI.Experimentsandsimulationsonultrasonicallyassisteddrilling[J].JournalofSoundandVibration,2007,308:815-830.

[3]CHERNG,LEEH.Usingworkpiecevibrationcuttingformicrodrilling[J].InternationalJournalofAdvancedManufacturingTechnology,2006,27(7-8):688-692.

[4] 林书玉,张福成.超声塑料焊接工具横向振动及其开槽的研究[J].声学技术,1992,11(4):24-28.

[5] 周光平,梁明军,王家宣.大尺寸超声振动体的研究[J].声学技术,2004,23(3):183-188.

[6] 林仲茂.超声变幅杆的原理和设计[M].北京:科学出版社,1987.

(编辑：庞富祥)

Design of Ultrasonic Vibration System in Ultrasonic Vibration Assisted Micro Machining

ZHAO Lei1,LIANG Xin1,LYU Ming1,WANG Shiying1,LIU Jiancheng1,2

(1.CollegeofMechanicalEngineering,TaiyuanUniversityofTechnology,Taiyuan030024,China;2.SchoolofEngineeringandComputerScience,Stockton95211,USA)

On the basis of the theory of one-dimensional longitudinal vibration, ultrasonic vibration system in ultrasonic vibration assisted micro machining was designed using the theoretical analytical method.The optimal solution about slot number of conical section and slit number of cylindrical section was determined by finite element software,which improves the uniformity of amplitude in workplace and enlarges the amplitude in workplace. The resonant frequency of vibration platform is reduced by increasing the length of conical section.The resonance characteristic of the system was investigated by modal analysis with the finite element software ANSYS,which meets the engineering requirements and verifies the feasibility of the design method.The study provides a convenient way to design large sized vibrators.

ultrasonic assisted micro machining;heoretical analytical method;finite element;resonant vibration character

1007-9432(2015)04-0371-04

2015-03-13

山西省自然科学基金资助项目：风冷式单层CBN砂轮超高速磨削机理的研究(2013011024-2)；山西省研究生优秀创新项目：超声珩点工程应用适应性研究(20133042)

赵蕾(1988-)，女，山西太原人，硕士生，主要从事超声辅助微细加工研究,(Tel)18734130622，(Email)zhaolei.jill@qq.com

吕明(1957-)，男，教授，博士生导师，(Email)lvming@tyut.edu.cn

TG544 TH113.1

A

10.16355/j.cnki.issn1007-9432tyut.2015.04.001