基于随机点扩散函数的多帧湍流退化图像自适应复原方法

朱瑞飞，魏　群*，王　超，贾宏光，吴海龙,2

(1.中国科学院 长春光学精密机械与物理研究所，吉林 长春130033；

2.中国科学院大学，北京 100049)



基于随机点扩散函数的多帧湍流退化图像自适应复原方法

朱瑞飞1，魏群1*，王超1，贾宏光1，吴海龙1,2

(1.中国科学院 长春光学精密机械与物理研究所，吉林 长春130033；

2.中国科学院大学，北京 100049)

摘要：针对湍流退化图像随机性的问题，提出了一种基于随机点扩散函数的多帧湍流退化图像自适应复原方法。首先介绍了随机点扩散函数的图像退化模型，并分析了点扩散函数随机性对图像复原造成的影响，建立了基于随机点扩散函数的多帧图像退化模型。在此基础上，建立了基于多帧退化图像的全变分复原模型，利用前向后向算子分裂法对模型进行求解，提高了算法的运算效率。然后，提出了一种新的自适应正则化参数选取方法，该方法利用全变分复原模型的目标函数计算正则化参数，当正则化参数收敛时，复原图像的峰值信噪比达到最大值，因此利用目标函数的相对差值作为自适应算法迭代终止的条件，可以获得最佳复原效果。最后通过实验分析，算法中退化图像的帧数应不大于10帧。实验结果表明：当取10帧退化图像时，AFBS算法运算时间与单帧的FBS算法相当，信噪比增益为1.4 dB。本文算法对图像噪声有明显的抑制作用，对湍流退化图像可以获得较好的复原效果。

关键词:图像复原；自适应正则化；随机点扩散函数；多帧模型；前向后向分裂算子；湍流退化图像

Adaptive restoration method of multi-frame turbulence-degraded

images based on stochastic point spread function

1引言

导弹作为目前高科技战争的主要武器，对目标特性获取的精确性及导弹时效性的依赖程度不断提高，因此，导弹多采用成像探测跟踪瞄准系统，而且飞行速度不断提高[1]。然而，带有成像探测系统的飞行器在大气层内高速飞行时，光学头罩与来流之间形成复杂的流场，引起目标图像偏移、抖动、模糊等气动光学效应[2]，从而严重影响导引头探测、识别和跟踪目标的能力[3-4]。从湍流退化图像中有效地复原出原目标图像，是实现超声速导弹成像探测及精确制导必须解决的关键问题之一[5]。

湍流退化图像复原的困难之处在于其点扩散函数是随机的[6]，这就导致利用湍流物理知识和退化图像先验知识估计得到的点扩散函数不能很好地复原出每一帧图像。基于多帧图像复原的方法可以在一定程度上提高湍流退化图像复原的稳定性，是目前主流的湍流退化图像复原方法。邵慧等人以退化序列中任意帧作为起始帧，逐次增加迭代帧，有效地提高了多帧算法的运算效率[7]。Hong等人利用连续两帧退化图像结合湍流的先验知识估计出图像退化的点扩散函数，获得了较好的复原效果[8]。这些方法都是从提高图像复原算法的运算效率出发，没有考虑湍流流场中图像的退化模型，所以算法的稳定性相对较差。

为了解决大气湍流点扩散函数随机性的问题，Ward提出了一种新的图像退化模型[9]，该模型考虑了湍流随机性的特点，能够较为准确地描述大气湍流对图像的影响。基于随机点扩散函数的图像退化模型被成功应用于均值滤波[10]、维纳滤波[12]以及全变分图像复原[12]，取得了一定的复原效果。但是这些方法在复原图像时都假设点扩散函数噪声是一个已知量，当点扩散函数噪声未知时，实际复原图像往往不能达到理想效果。Jung等人将随机点扩散函数的图像退化模型应用于多帧的全变分图像复原中，当点扩散函数噪声未知时，获得了高质量的复原图像[13]。

本文根据湍流退化图像随机性的特点，提出了一种基于随机点扩散函数的多帧湍流退化图像自适应复原方法。为了减小点扩散函数随机性给图像复原带来的困难，该方法首先建立了多帧图像退化模型，在此基础上，建立了基于多帧退化图像的全变分复原模型。为了提高算法的运算效率，采用前向后向算子分裂法(Forward-backward Splitting，FBS)对模型进行了求解。针对传统正则化参数选取方法的不足，提出了利用模型目标函数自适应地计算正则化参数的方法，并通过实验证明了当正则化参数收敛时，复原图像的峰值信噪比(PSNR)达到最大，从而给出了算法迭代终止的条件。

2基于随机点扩散函数的多帧图像退化模型

2.1　随机点扩散函数模型

受Ward的启发，图像退化的一般数学模型可以改写为：

(1)

式中：观测时间t∈[0,T]，点扩散函数h(x,y,t)以及噪声n1(x,y,t)都是随时间随机变化的，所以退化图像也是随时间变化的。这里假设h(x,y,t)随时间变化的均值是已知的，即:

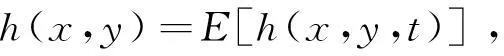
(2)

这样，式(1)可以写成如下形式：

(3)

(4)

(5)

本文把n2(x,y,t)称为点扩散函数h(x,y)的噪声，式(3)~(5)称为图像退化的随机点扩散函数模型。

以国际标准测试图像Lena为例，分析点扩散函数噪声对观测图像的影响，原始图像如图1(a)所示。n2(x,y,t)是一个均值为0的高斯噪声，方差分别取0.001，0.01，0.1，h(x,y)是一个大小为11×11的高斯模糊核，不考虑噪声n1(x,y,t)。对原始图像退化处理后得到如图1(b)、1(c)、1(d)所示模糊图像。

图1　点扩散函数噪声对观测图像的影响 Fig.1　Influence of the noise of the PSF on the blurred images

从图1中可以看出，点扩散函数噪声n2(x,y,t)对观测图像的质量影响很大，点扩散函数噪声越大，图像的质量越差。应用全变分正则化复原方法分两种情况对图1中退化图像进行复原，第一种情况点扩散函数噪声已知，第二种情况点扩散函数噪声未知，复原结果分别如图2和图3所示。

图2　点扩散函数噪声已知时图像复原结果 Fig.2　Results of image restoration with known n2

图3　点扩散函数噪声未知时图像复原结果 Fig.3　Results of image restoration with unknown n2

从图2和图3可以看出，当点扩散函数噪声已知时，图像能获得非常好的复原效果；当点扩散函数噪声未知时，复原效果较差，尤其是噪声较大时，复原图像的质量甚至低于退化图像。因此，从随机的湍流退化图像中直接获得高质量的复原图像是非常困难的。

2.2　多帧图像退化模型

在随机点扩散函数模型的基础上，提出了多帧图像退化模型，其表达式为：

(6)

(7)

式中：k=1,2,…,N，N为所取的连续图像的帧数。对于N帧连续图像，其平均图像的定义为：

(8)

将式(6)和式(7)代入式(8)中可得：

(9)

(10)

(11)

3基于FBS的自适应正则化图像复原

3.1　基于多帧退化图像的全变分正则化模型

Rudin和Osher提出的全变分图像复原模型[14]因为其具有明显的各向异性扩散的特性，被认为是目前较为合理的能够保持图像边缘特征的图像模型，公式如下：

(12)

(13)

(14)

(15)

3.2　前向后向算子分裂法

前向后向算子分裂法是一种分而治之的方法，能够将复杂问题分解为一系列简单项子问题进行求解[15]，经常用来求解包含光滑保真项和非光滑惩罚项的优化问题，具有很好的收敛性[16]。如果函数f0(Ω)，对于任意x∈Ω，最小化问题:

(16)

存在唯一最小解，称这个最小解为函数f的邻近算子，记为proxf。邻近算子具有非常严格的非扩张特性，非常适合迭代最小化的算法求解。

对于式(17)所示的凸最优问题：

(17)

如果f1∈Γ0(Ω)，f2∈Ω满足利普西茨连续可微条件，那么对于∀(x,y)∈Ω，有

(18)

式中：β∈(0,+∞)是f2的利普西茨常数。这时，式(17)的最优解为：

(19)

式(19)写成迭代的形式：

(20)

式中：步长参数γn是一个满足有界区间[γmin,γmax]的序列，即:

(21)

FBS算法的第一步迭代是对函数f2(x)进行梯度下降操作，是显式的迭代格式；第二步迭代是求解f1(x)的邻近算子，是隐式的迭代格式。FBS算法是联合了两种基本的迭代格式的方法，算法不需要求解整个目标函数的邻近算子，从而降低了求解难度，同时又保持了隐式的迭代格式，保证了算法的收敛性，

但是使用FBS求解模型时，其中一项必须满足利普西茨可微条件，所以应用范围有一定的局限性。

利用FBS求解式(12)的全变分正则化模型，算法执行过程如表1所示。

表1　FBS算法执行步骤

序列{αn}是松弛因子，定义为：

(22)

3.3　基于FBS的自适应正则化图像复原

在正则化图像复原的方法中，正则参数的选取非常关键，其在很大程度上决定了复原图像的质量。正则参数起着平衡保真项和正则项的作用，参数过小时，复原模型的平滑性较差，去噪效果不佳，甚至在图像中产生块状的失真，参数过大时，正则项在模型中占的比重就大，平滑效果虽好，但是图像的纹理细节也同样被平滑掉了，造成图像信息丢失。

目前，正则化参数的自适应选择方法主要有广义交互验证法(Generalized Cross-Validation，GCV)[17]和L曲线法[18]。GCV利用统计学方法，无需噪声方差的先验知识，但是GCV法不能实现全局最优，L曲线法的收敛性比GCV法差，计算量更大。为了提高运算效率，在压缩感知理论中经常采用序贯策略选择合适的正则参数，即预先规定正则参数的初值和迭代终止的最小值，然后选取合适的下降方法使正则参数逐渐减小，较大正则参数时的模型最优解作为下一次迭代的初始解，直到正则参数下降到预设的最小值时停止迭代。一般按照如下经验公式计算：

(23)

式中:r∈(0,1)是减缩因子。采用这种方法选取γ，保证了正则参数单调递减，同时可以提高算法的收敛速度，但是这种方法无法自适应地找到合适的λ1、λmin以及减缩因子r，这几个参数能否合理的选择直接影响着算法复原效果和运算效率。利用FBS算法对Lena退化图像进行复原，图4是按照式(23)选取正则参数时，复原图像的PSNR随正则参数的变化关系。

图4　选择不同减缩因子时PSNR与λ的关系 Fig.4　PSNR versus λ by choosing different r

从图4中可以看出，减缩因子越小，算法收敛的速度越快，但复原效果也越差，所以选择合适的下降规律尤为重要；随着正则参数的减小，PSNR先增加后减小，因而找到一种合适的迭代停止条件不仅可以获得最佳的复原图像，还可以减少算法的运算时间。本文提出一种新的利用全变分正则化模型的目标函数自适应地选取正则参数的方法，目标函数定义如下：

(24)

式中：

(25)

正则参数的计算公式为：

(26)

容易证明，目标函数是凸函数，而且是λk的单增函数，即当F(λk,uλk)减小时，λk随之减小，保证了算法的收敛性。

分别用两种不同正则参数选取方法对Lena退化图像复原，第一种方法作为参考方法，λ从λ1=0.5依次减小0.001，进行500次迭代，第二种方法按照式(26)计算正则参数，取λ1=0.5,λ2=0.4，同样进行500次迭代，复原过程中PSNR和F(λ,μλ)随正则参数λ的变化曲线如图5所示。

图5　两种正则参数选取方法比较 Fig.5　Comparison of two selection methods of regularization parameter

从图5(a)可以看出，使用本文方法复原的图像，PSNR随正则参数λ的减小快速增大，并收敛到最大值，图像获得最佳复原效果，而目标函数F(λ,uλ)在迭代过程中能快速收敛，因此可以用连续两次迭代中F(λ,uλ)的相对差值作为迭代终止的判定条件，这样就避免了由于λmin选取不合适造成的复原效果不佳以及迭代次数多的问题。定义循环迭代终止的条件为：

(27)

显然，算法中λ1和λ2的选取不能通过式(26)计算，本文用退化图像作为初值计算λ1，即：

(28)

式中：权系数一般取0

(29)

如果λ2≥λ1，那么取λ2=0.8λ1。

为了进一步提高自适应算法的计算效率，将算法FBS中的内外两层迭代合并为只有一层迭代，算法执行步骤如表2所示。

表2　AFBS算法执行步骤

4实验结果与分析

为了验证本文算法对湍流退化图像的复原效果，本文在Matlab2012软件环境条件下进行了复原实验，实验所使用的计算机配置为：处理器是Intel(R) Core(TM) i5-2450M CPU，主频是2.5 GHz，内存是2 GB。

4.1　复原效果比较实验

图6　复原效果比较 Fig.6　Restoration effect comparison

图7　ISNR随帧数k的变化曲线 Fig.7　Curves of ISNR vs. k

实验一的目的是从图像的复原效果和实时性两方面验证本文自适应算法。原始Satellite图像如图6(a)所示，通过仿真得到序列湍流退化图像，图6(b)是其中一帧退化图像。分别用单帧图像的FBS算法和AFBS算法以及多帧图像的FBS算法和AFBS算法进行了图像复原实验，其中FBS算法所选参数为：λ1=0，λmin=0.000 1，r=0.8，niter=10；AFBS算法迭代终止条件为：reldiff=0.000 1。复原结果如图6(c)~6(h)所示。从图中可以看到，随着帧数k的增加，FBS算法和AFBS算法图像复原效果越来越好，而且多帧的算法对噪声有明显的抑制作用。复原图像信噪比增益(ISNR)随帧数k的变化曲线如图7所示，ISNR随着帧数k的增大而增大，当k>10时，ISNR的增幅变缓，AFBS算法的ISNR明显大于FBS算法。算法的运算时间随帧数k的变化曲线如图8所示，运算时间随着帧数k的增大而增大，FBS算法运算时间大于AFBS算法。综合考虑复原效果和运算效率，退化图像的帧数应小于10帧。

图8　运算时间随帧数k的变化曲线 Fig.8　Curves of time vs. k

4.2　实际湍流退化图像复原实验

实验二利用AFBS算法对实际湍流退化图像进行复原，图9是连续10帧湍流退化图像，图10是单帧图像和多帧图像的复原结果，图11是复原图像的局部放大图。从图中可以看出，本文复原方法复原的图像边缘细节清晰，与单帧图像的复原方法相比，图像的复原效果更加明显。

图9　湍流退化图像序列 Fig.9　Turbulence-degraded images sequence

图10　湍流退化图像复原效果 Fig.10　Restoration effect of turbulence-degraded images

图11　退化/复原图像局部放大图 Fig.11　Close-ups of degraded/restored image regions

5结论

本文提出了一种基于随机点扩散函数的多帧湍流退化图像自适应复原方法。该方法首先根据湍流随机性的特点，建立了基于随机点扩散函数的多帧图像退化模型，并证明了模型的正确性，通过实验验证了点扩散函数随机性给图像复原造成的困难。在此基础上，建立了基于多帧退化图像的全变分复原模型，利用FBS将复原模型分解为两个简单的子问题进行求解，提高了算法的计算效率。然后重点研究了正则化参数的选取方法，建立了正则化参数与模型目标函数的关系，提出了基于FBS的自适应正则化图像复原算法。综合考虑图像复原效果和算法运算时间，退化图像的帧数应不大于10帧。实验结果表明：当退化图像取相同的帧数时，AFBS算法运算时间比FBS算法减少了10%以上，PSNR提高了0.6~0.8 dB；当取10帧退化图像时，AFBS算法运算时间与单帧的FBS算法相当，ISNR为1.4 dB。本文算法对图像噪声有明显的抑制作用，对实现湍流退化图像的复原具有一定的理论和应用价值。

参考文献：

[1]魏群，艾兴乔，姜湖海，等.超音速光学导引头整流罩的形状优化[J].光学 精密工程,2010,18(2):384-389.

WEI Q,AI X Q,JIANG H H,etal.. Optimizing design of dome figure for supersonic seekers[J].Opt.PrecisionEng.,2010,18(2):384-389.(in Chinese)

[2]殷兴良.气动光学原理[M].北京：中国宇航出版社，2003.

YIN X L.PrincipleofAero-Optics[M]. Beijing：China Astronautics Press，2003.(in Chinese)

[3]费锦东.高速红外成像末制导对气动光学效应技术研究的需求[J].红外与激光工程,1998,27(1):42-51.

FEI J D. Study on aero-optical effect technology for high speed missile infrared image guide[J].InfraredandLaserEngineering,1998,27(1):42-51.(in Chinese)

[4]姜振海，王超，魏群，等.超音速共形整流罩风洞试验及其光机特性[J].光学 精密工程,2012,20(9):2000-2005.

JIANG ZH H,WANG CH,WEI Q,etal.. Wind tunnel experiment of supersonic conformal dome and its optical and structure characteristic[J].Opt.PrecisionEng.,2012,20(9):2000-2005.(in Chinese)

[5]张士杰，李俊山，杨亚威，等.湍流退化红外图像降晰函数辨识[J].光学 精密工程,2013,21(2):514-521.

ZHANG SH J,LI J SH,YANG Y W,etal.. Blur identification of turbulence-degraded IR images[J].Opt.PrecisionEng.,2013,21(2):514-521.(in Chinese)

[6]张天序，洪汉玉，孙向华，等.基于估计点扩展函数值的湍流退化图像复原[J].自动化学报,2003,29(4):573-581.

ZHANG T X,HONG H Y,SUN X H,etal.. Restoring turbulence-degraded images based on estimation of turbulence point spread function values[J].ActaAutomaticaSinica,2003,29(4):573-581.(in Chinese)

[7]邵慧，汪建业，王亮，等.基于循环迭代的多帧湍流退化图像复原算法[J].激光与光电子学进展,2014,51:071002.

SHAO H,WANG J Y,WANG L,etal.. Multiframe turbulence-degraded image restoration algorithm based on circulate iteration[J].Laser&OptoelectronicsProgress,2014,51:071002.(in Chinese)

[8]HONG H Y,LI L C,ZHANG T X. Blind restoration of real turbulence-degraded image with complicated backgrounds using anisotropic regularization[J].OpticsCommunications,2012,285:4977-4986.

[9]WARD R K,SALEH B E A. Restoration of images distorted by systems of random impulse response[J].J.Opt.Soc.Amer.A,1985,2(8):1254-1259.

[10]GUAN L,WARD R K. Restoration of stochastically blurred images by the geometrical mean filter[J].Opt.Eng.,1990,29(4):289-295.

[11]GUAN L,WARD R K. Restoration of randomly blurred images by the Wiener filter[J].IEEE,1989,36:589-592.

[12]MESAROVIC V Z,GALATSANOS N P,KATSAGGELOS A K. Regularized constrained total least-squares image restoration[J].IEEE,1995,4(8):1096-1108.

[13]JUNG M,MARQUINA A,VESE L A. Variational multiframe restoration of images degraded by noisy(stochastic) blur kernels[J].J.ComputationalandAppliedMathematics,2013,240:123-134.

[14]RUDIN L,OSHER S,FATEM I E. Nonlinear total variation based noise removal algorithms[J].PhysicaD,1992,60(1.4):259-268.

[15]孙玉宝，费选，韦志辉，等.基于前向后向算子分裂的稀疏性正则化图像超分辨率算法[J].自动化学报,2010,36(9):1232-1238.

SUN Y B,FEI X,WEI ZH H,etal.. Sparsity regularized image super-resolution model via forward-backward operator splitting method[J].ActaAutomaticaSinica,2010,36(9):1232-1238.(in Chinese)

[16]COMBETTES P L,WAJS V R. Signal recovery by proximal forward-backward splitting[J].SIAMJ.MultiscaleModel.Simul.,2005,4(4):1168-1200.

[17]GOLUB G H,MATT U V. Generalized cross-validation for large-scale problems[J].J.ComputationalandGraphicalStatistics,1997,6(1):1-34.

[18]张彬，倪国强.一种基于曲线准则的正则化图像复原算法[J].北京理工大学学报,2014,34(6): 627-632.

ZHANG B,NI G Q. Regularized image restoration algorithm based on the L-curve criterion[J].TransactionofBeijingInstituteofTechnology,2014,34(6):627-632.(in Chinese)

朱瑞飞(1986—)，男，山西朔州人，助理研究员，2009年于吉林大学获得学士学位，2014年于中国科学院长春光机所获得博士学位，主要从事红外图像处理方面的研究。E-mail:zhuiruifei1105@163.com

魏　群(1983—)，男，黑龙江哈尔滨人，副研究员，2005年于浙江大学获得学士学位，2010年于中国科学院长春光机所获得博士学位，主要从事共形光学及气动光学方面的研究。E-mail:wei.q@hotmail.com

王　超(1984—)，男，黑龙江哈尔滨人，助理研究员，2010年于中国地质大学(武汉)获得工学硕士学位，主要从事仪器仪表技术方面的研究。E-mail:wc100714@163.com

贾宏光(1971—)，男，黑龙江省五常人，研究员，博士生导师，2000年于中国科学院长春光学精密机械与物理研究所获得博士学位，主要从事光机电系统微小型化与精确制导技术方面的研究。E-mail:jiahg@ciomp.ac.cn

吴海龙(1988—)，男，山东济南人，博士研究生，2011年于中国石油大学(华东)获得学士学位，主要从事控制系统设计方面的研究。E-mail:wuhailong.2001@163.com

ZHU Rei-fei1, WEI Qun1*, WANG Chao1, JIA Hong-guang1, WU Hai-long1,2

(1.ChangchunInstituteofOptics,FineMechanicsandPhysics,

ChineseAcademyofSciences,Changchun130033,China；

2.UniversityofChineseAcademyofSciences,Beijing100049,China)

Abstract:As the turbulence-degraded images are stochastic, an adaptive restoration approach of multi-frame turbulence-degraded images was proposed based on stochastic Point Spread Function(PSF). Firstly, an image degradation model of stochastic PSF was introduced, and the influence of the model on the image restoration was analyzed. The degradation model of multi-frame images based on stochastic PSF was established. On this basis, the TV restoration model based on multi-frame images was established. In order to improve the computational efficiency of the algorithm, the model was solved by Forward-Backward Splitting(FBS) operator. Then a new adaptive selection method of regularization parameter was proposed. When the regularization parameter which was calculated by the objective function of the TV model was convergent, the Peak Signal-to-Noise Ratio(PSNR) of restoration image reached the maximum value. In order to get the best restoration effect, the relative error of the objective function was used as the iterative termination condition of the adaptive algorithm. Finally, the number of degraded images should be no more than 10 frames through the experimental analysis. Experimental results show that the ISNR of the AFBS algorithm has increased 1.4 dB more than the FBS algorithm based on single frame while the computing time is comparative when the number of degraded images was 10 frames. The proposed algorithm has an obvious inhibition on the noises, and it can obtain a better restoration effect on turbulence-degraded images.

Key words:image restoration;adaptive regularization;stochastic point spread function;multi-frame model;forward-backward splitting;turbulence-degraded image

作者简介：

*Corresponding author, E-mail:wei.q@hotmail.com

中图分类号：TP391.4

文献标识码:A

doi:10.3788/CO.20150803.0368

文章编号2095-1531(2015)03-0368-10

基金项目：装备预研基金资助项目(No.51301060207)

收稿日期:2014-11-15；

修订日期:2015-02-16