海上间瞄射击控制技术分析和仿真

武智晖，马红卫，梁建奇，张卫民

（1.中国兵器科学研究院，北京100089；2.中国兵器工业导航与控制技术研究所，北京100089）

海上间瞄射击控制技术分析和仿真

武智晖1，马红卫2，梁建奇2，张卫民2

（1.中国兵器科学研究院，北京100089；2.中国兵器工业导航与控制技术研究所，北京100089）

针对自行火炮海上自动间瞄瞄准问题，分析了海浪对火炮身管扰动的规律，建立了相应的数学模型，对火炮随动系统进行了功率需求分析和优化设计，并在特定海况条件下进行了仿真。分析和仿真结果表明，在现有火炮的基础上，针对海浪扰动适当增加随动系统的输出功率，对随动系统进行改进设计，根据火炮位置变化实时更新射击诸元，可以使火炮在海浪扰动条件下达到间瞄射击所要求的瞄准精度。

自动控制，间瞄瞄准，海浪扰动，随动系统

0 引言

在现有自行火炮（以下简称火炮）的基础上，合理设计火炮的随动系统，使火炮在运输船舰上能达到间瞄射击所要求的瞄准精度，实现海上自动瞄准射击，对于未来战争中的登陆（岛）作战具有重大意义。实现火炮在渡海过程中的瞄准射击，主要需要解决海浪波动对火炮身管的扰动问题。

1 有关定义［1］

定义1：炮塔坐标系O-X1Y1在1——设炮塔回转中心为坐标原点O，X1轴为火炮身管与车体纵轴同向时火炮轴线在炮塔回转平面的投影，向前为正；在1轴沿炮塔回转平面法线向上，Y1轴向右，OX1Y1在1构成左手坐标系。

定义2：炮塔纵倾角ψ——炮塔坐标系X1轴与水平面之夹角，前倾为正。

定义3：纵倾平面——炮塔坐标系Y1轴水平，X1轴与水平面之夹角为ψ时的炮塔回转平面。

定义4：炮塔横倾角r——炮塔坐标系Y1轴与纵倾平面之夹角，沿炮轴线向前看，右倾为正。

定义5：炮塔水平坐标系O-X0Y0在0——当ψ=γ=0时的炮塔坐标系。

定义6：炮塔方位角——炮塔座圈旋转的角度，火炮轴线与车体同向时为0。

2 火炮随海浪摇摆的数学模型

在海上航行时，海浪将对火炮产生6自由度的扰动，其中对火炮间瞄射击影响最大的是火炮随海浪的横摇和纵摇。由于海浪的复杂性和随机性，很难用一个数学模型对其进行精确描述，不同型号的运输舰船随海浪摇摆的规律也不尽相同。为分析方便，假设海浪仅对火炮产生横摇和纵摇扰动，且炮塔纵倾角ψ和炮塔横倾角γ随海浪的变化规律可用正弦函数描述［2］

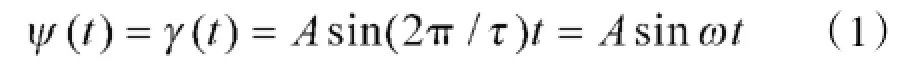
根据上述假设，可得炮塔姿态角随海浪变化时最大角速度为：

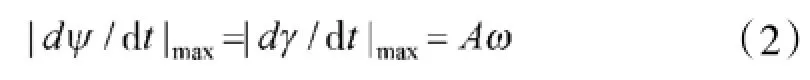
最大角加速度为：

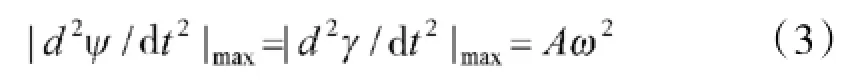
需要说明的是，当海浪为纵浪时炮塔纵倾角摇摆大，横浪时炮塔横倾角摇摆大，二者不会同时达到最大值。

3 海浪对火炮身管指向的扰动分析

根据前面的假设，火炮理想射击诸元可在炮塔水平坐标系下给定。当炮塔纵倾角和横倾角随海浪变化时，受其影响火炮身管指向在炮塔水平坐标系下产生位移。设火炮在炮塔坐标系下高低角为ε1、方位角为β1=0（）；又设炮塔水平坐标系下火炮的单位向量为{X0，Y0，在0}，则有：

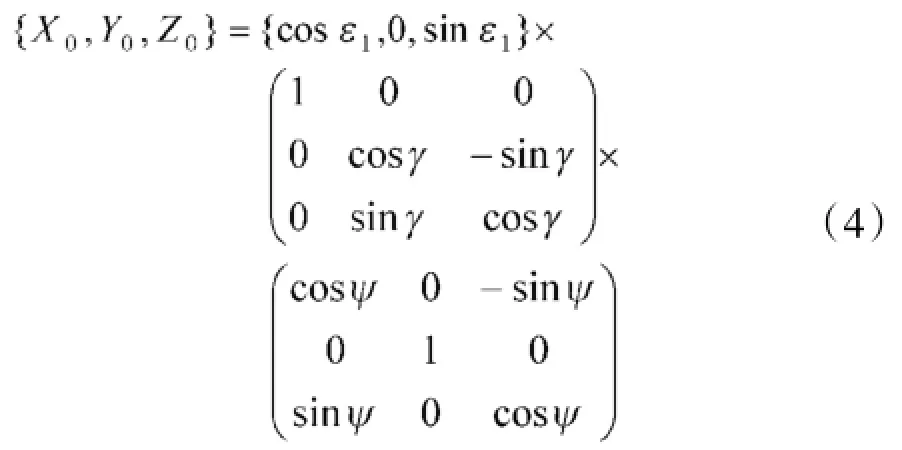
设β0、ε0分别为身管在炮塔水平坐标系下的方位角、高低角，则由式（4）有：

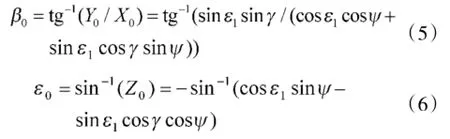
式（5）、式（6）描述了在炮塔水平坐标系下火炮身管指向与炮塔姿态角的关系。由式（5）易知，高低角ε1越大，海浪对火炮方位方向的扰动就越大。为讨论方便，且不失一般性，在以下分析中取ε1=π/4。

下面分别讨论海浪为纵浪和横浪的情况。海浪为纵浪时，假设炮塔纵倾角随海浪波动，横倾角为0，由式（5）、式（6）可得

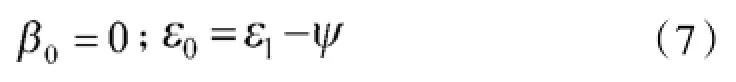
即在炮塔水平坐标系下，火炮高低方向随海浪运动，方位方向没有扰动。

海浪为横浪时，假设炮塔横倾角随海浪波动，纵倾角为0，并注意到当γ≤π/18时，sinγ≈tgγ≈γ，cosγ≈1，以及当ε1=π/4时，tgε1=1，由式（5）、式（6）可得：

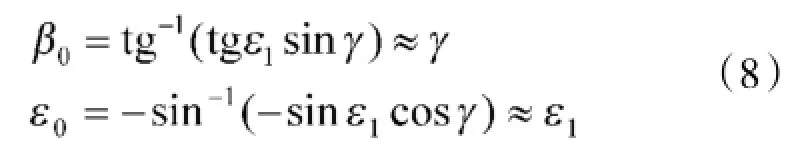
即在炮塔水平坐标系下，火炮方位方向随海浪运动，高低方向扰动较小。

由式（2）、式（3）、式（7）、式（8）可得受海浪扰动时，火炮在炮塔水平坐标系下方位和高低方向最大角速度和最大角加速度：

4 调炮所需的最大角速度和角加速度

海浪的扰动使火炮身管指向在炮塔水平坐标系中产生偏移，而火炮的随动电机是在炮塔坐标系中控制火炮抵消海浪的扰动。因此，需计算为抵消扰动，身管在炮塔坐标系下需要的最大角速度和最大角加速度，以此作为估算电机最大力矩的条件。

在高低方向，由式（7）可知，若保持ε0不变，需满足ε1=ψ，进而有

在方位方向，当γ≤π/18时，也近似有（略去推导）

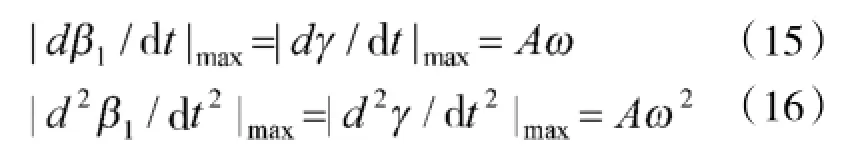
5 随动系统功率需求分析

5.1 随动系统负载分析

火炮随动系统的负载转矩包括惯性转矩、摩擦力矩和不平衡力矩。在以下讨论中，设θ为随动系统电机轴的角位移，ηc为齿轮传动效率，j为随动系统减速比。

a）惯性转矩

设TL为折合到电机轴上的负载惯性转矩，则有：

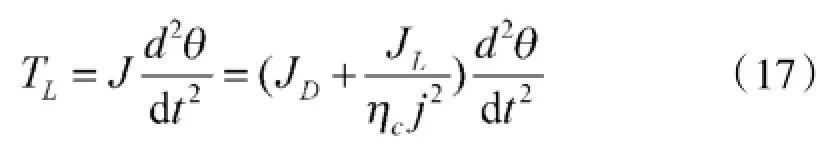
其中J为电机和负载折合到电机轴上的转动惯量，JL为负载的转动惯量，JD为电机的转动惯量。

b）摩擦力矩

设Tf为折合到电机轴上的摩擦力矩，则有：

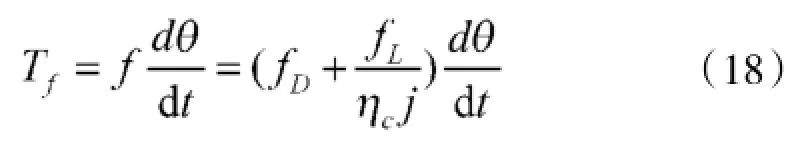
其中，f为电机和负载折合到电动机轴上的粘性摩擦系数，fL为负载的粘性摩擦系数，fD为电机的粘性摩擦系数。

c）不平衡力矩

设Tm为折合到电机轴上的炮塔倾斜产生的不平衡力矩，则有：

其中Tm*为炮塔倾斜产生的不平衡力矩。

5.2 随动系统输出转矩计算

设Tw为随动系统电机输出的转矩，则火炮在海浪中可控的必要条件为：

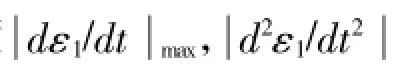
6 海上间瞄射击时火炮控制方案及仿真

传统的间瞄火炮由于射击时处于静止状态，其随动系统采用位置环控制即可实现自动调炮瞄准。在海上射击时，为克服海浪的扰动，需要在已有位置环的基础上引入速度环，在速度环中采用惯性器件作为角速度传感器。

以某自行火炮为对象，方位随动系统原理如图1所示：

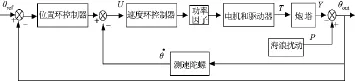
图1火炮方位随动系统原理框图

图1 中θref为炮塔水平坐标系下给定的方位调炮诸元，θout和θ˙分别为炮塔水平坐标系下火炮的方位角和方位角速度，Y为炮塔方位角，P为海浪扰动。

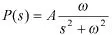
其中

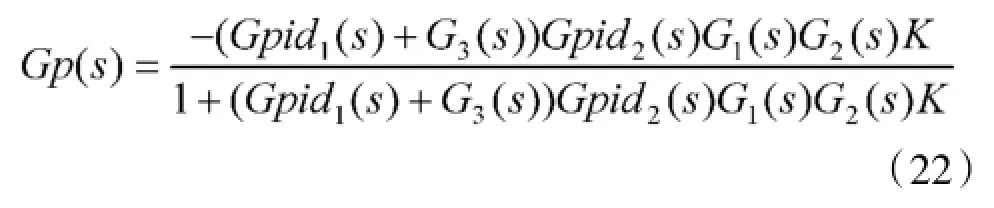
即输入为海浪扰动，输出为炮塔方位角的闭环传递函数。为抵消海浪扰动P，炮塔方位角输出Y应为与P相位相差180°，且幅值相同的正弦波。

为了设计最佳的位置环控制器Gpid1（s）和速度环控制器Gpid2（s），在MATLAB的Control and Estimation界面中将Gpid1（s）、Gpid2（s）两环节作为可调整环节，代入某自行火炮的参数，通过调整两环节的参数得出闭环传递函数Gp（s）的理想幅频和相频曲线如图2所示。

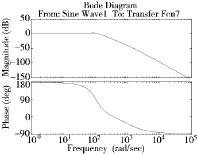
图2 方位随动系统理想幅频和相频曲线

由此得到调整后Gpid1（s）、Gpid2（s）两环节的最佳参数。

将海浪参数、火炮参数、控制器设计参数等代入图1所示的系统，在MATLAB的simulink中仿真，得到输入θref=0.52 rad（即方位调炮约30°）时系统的阶跃响应结果θout为：

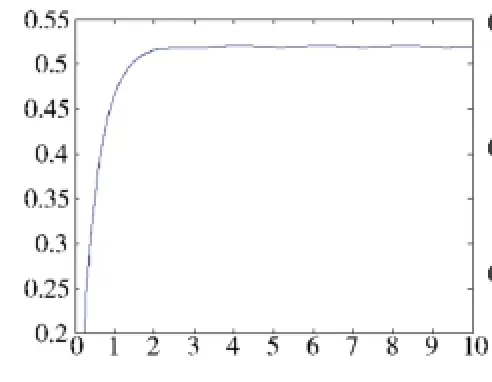
图3 方位随动系统阶跃响应结果θout（0～10 s）

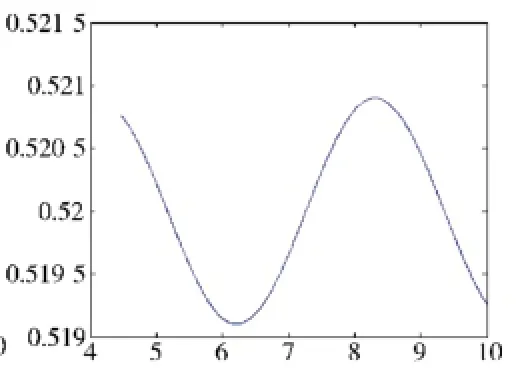
图4 方位随动系统阶跃响应结果θout（4 s～10 s）

图3和图4表明，在三级海况条件下，火炮方位调炮30°时方位随动系统达到瞄准精度的时间小于4 s，4 s后系统稳定误差小于1 mrad。

7 结论

本文分析了海浪对火炮身管扰动的规律，建立了相应的数学模型，计算了随动系统的输出转矩，对火炮随动系统进行了优化设计，并在特定海况条件下进行了仿真。分析和仿真结果表明，在现有火炮的基础上，针对海浪扰动适当增加随动系统的输出功率，对随动系统进行优化设计，并根据火炮位置变化实时更新射击诸元，可以使火炮在海浪扰动条件下达到间瞄射击所要求的瞄准精度。

［1］陶化成.一个新的压制兵器自动操瞄控制方案［J］.兵工学报，1997，18（1）：9-14.

［2］居乃鵕.两栖车辆水动力学分析与仿真［M］.北京：兵器工业出版社，2005.

Analysis and Simulation of Offshore Indirect Firing Control Technology

WU Zhi-hui1，MA Hong-wei2，LIANG Jian-qi2，ZHANG Wei-min2
（1.China Academy of Weapon Science，Beijing 100089，China；
2.China Institute of Weapon Industry Navigation and Control Technology，Beijing 100089，China）

Taking aim at the problem of self-propelled artillery offshore automatic indirect aim，the rule of the disturbance on artillery barrel by sea wave is analyzed，the corresponding mathematical model is established.The artillery servo system is analyzed and optimized design of power demand，and is simulated in particular sea conditions.Analysis and simulation results show that on the base of the existing artillery，appropriate increasing the output power of the servo system according to sea wave disturbance，and improving the design of the servo system，can make the artillery in the sea wave disturbance conditions achieve indirect aiming accuracy required.

automatic control，indirect aim，sea wave disturbance，servo system

TJ399

A

1002-0640（2015）01-0077-03

2013-11-05

2014-12-07

武智晖（1979-），男，山西交城人，硕士。研究方向：光电火控。