舰载武器系统可靠性模型及其探索性研究

王勤，黄力伟，苏琦

（海军大连舰艇学院，辽宁大连116018）

舰载武器系统可靠性模型及其探索性研究

王勤，黄力伟，苏琦

（海军大连舰艇学院，辽宁大连116018）

从系统可靠性、任务可靠性、通道可靠性3个方面，通过模型分析、影响分析和参数讨论对武器系统可靠性进行探索性研究，并给出研究结论，阐述了三者的关系和对武器系统效能发挥的影响，为提高武器系统效能决策研究提供了理论依据。

武器系统可靠性，串并联系统，探索性研究

1　武器系统可靠性与探索性研究

1.1系统可靠性、任务可靠性和通道可靠性

以任务完好性为中心的装备保障研究中，可靠性是一个非常重要的指标［1］。可靠性是指元件、产品、系统在一定时间内、在一定条件下无故障的执行指定功能的能力或可能性。对于武器系统而言，可靠性又称为工作可靠性，可由固有可用度和任务可靠度来表示。如果定义一个武器系统的可靠性为Kk，其固有可用度为A，任务可靠度为R，则有如下表达式：

根据表现形式不同，武器系统可靠性可分为系统可靠性、通道可靠性和任务可靠性。

系统可靠性［2］是指武器系统的基本可靠性，指系统本身能工作的可信赖程度，受系统设计和研制影响，系统一旦研制成功并列装，其基本可靠性初始值就能确定。

任务可靠性是指武器系统按要求完成该任务的可能性，任务可靠性大小由执行任务的系统体系结构和系统可靠性值确定。

任务体系结构是由完成任务的一个个武器系统通道组成，通道是武器系统发挥功能的一个串联系统结构，一般的武器通道由“探测系统-指控系统-武器系统”组成，显然通道可靠性的大小也是由系统可靠性值确定。

1.2探索性研究

探索性分析是对大量不确定性因素的一个整体研究，使得决策分析更加灵活、高效，并且具有较强的适应性［3］。本文借鉴这一思想，在原始数据缺乏的情况下，采用系统分析的思想，综合使用“解析模型+概率模型+初始数据+参数讨论”方法对武器系统可靠性进行探索，目的是通过研究发现规律，以期对舰载武器系统装备保障研究提供有益的思考。

2　武器系统可靠性模型

2.1系统可靠性轨迹

根据参考文献［2］，可以确定典型舰载武器系统的初始固有可用度和任务可靠度参考值，见表1。

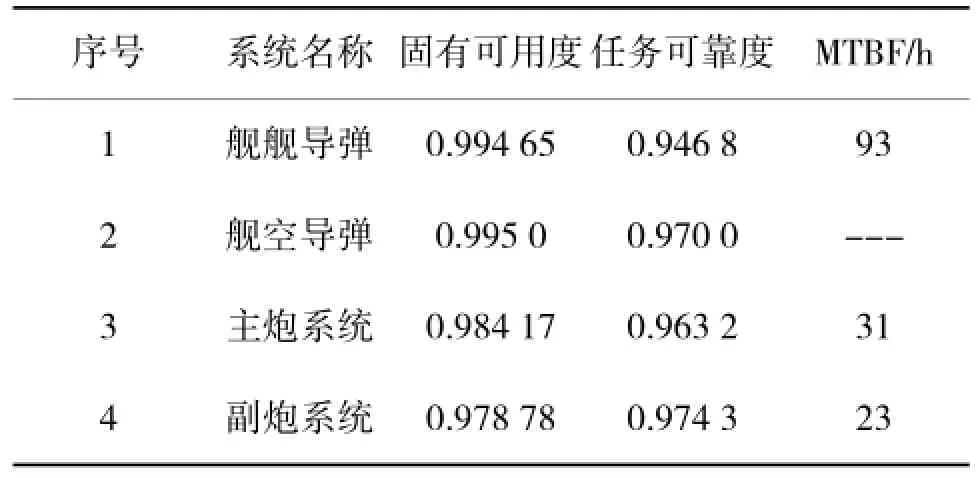
表1　舰载系统固有可用度和任务可靠度初始值

随着系统工作时间的增加，系统的固有可用度和任务可靠度都会下降，系统可靠性会下降，而且这种下降不是线性下降的，定义系统固有可用度和任务可靠度的下降强度为λ，根据可靠性指数分布特性的普遍性，可以认为固有可用度和任务可靠度的下降具备指数特性，即：

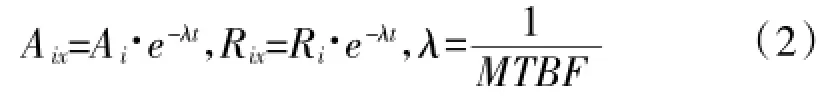
由此可得到舰载典型武器系统的可靠性轨迹，如图1所示。

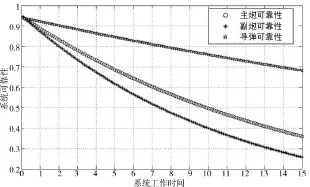
图1　典型武器系统可靠性轨迹

由图1得出：①系统可靠性都是单调指标，随着系统工作时间增长，呈现出“越来越小”的趋势；②舰舰导弹可靠性高于主副炮可靠性，主炮可靠性高于副炮可靠性；③随着系统工作时间增长，主副炮可靠性的下降趋势大于舰舰导弹。

2.2基于串并联系统的武器系统任务可靠性模型

作战任务是在一定的指令下，由舰载系统去完成，如果按照执行任务的系统去对任务进行分解，一般情况下，一个作战任务的完成可由如图2所示的系统去完成。

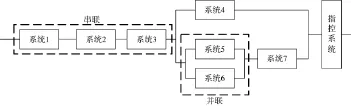
图2　任务分解的系统构成图

在图2中，存在两种结构：串联结构和并联结构。假设完成任务的系统数量有n个，第i个系统的初始固有可用度和任务可靠度分别为Ai、Ri，则串联系统和并联系统的固有可用度计算和任务可靠度计算公式为［4］：

（1）串联系统

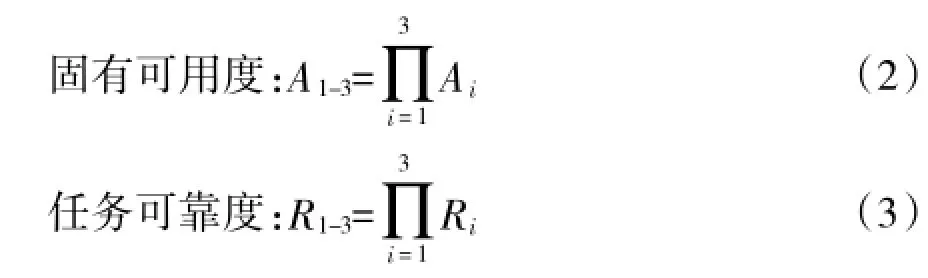
（2）并联系统

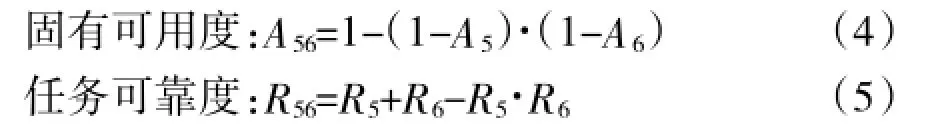
由此得到图2所示的任务可靠性的固有可用度和任务可靠度计算公式。假设指控系统为系统8。

（1）固有可用度

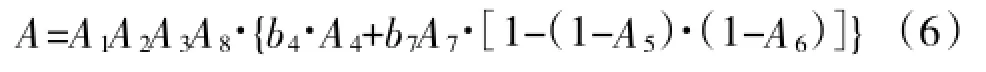
（2）任务可靠度

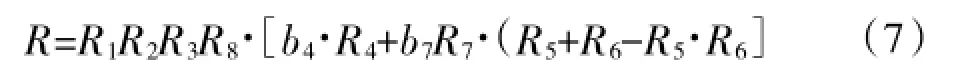
式中，b4、b7指的是武器系统的任务比率，同时也表明系统4和系统7为武器系统。

2.3通道可靠性模型

因为武器系统通道一般都是串联系统，因此，通道可靠性可采用串联系统的固有可用度和任务可靠度式（2）和式（3）进行计算。

2.4可靠性影响模型

影响指的是指标使武器系统效能向好的方向或坏的方向变化，或者不发生改变。假设某一武器系统的标准效能值是Xlb，受到指标影响后的效能为Xlg，则可以采用以下几种方式来表示指标对武器系统效能的影响。

根据不同的指标分析需求可以分别采用（1）、（2）来进行影响表示。如果采用影响距离来表示指标体系中的指标对武器系统的影响，n取值为2。

如表1所示，获得了系统的初始固有可用度和任务可靠度数据，则可获得某一任务可靠性的初始值（或者最大值），这个值可作为可靠性的标准值，假设为Kk。当各系统执行任务之后，其固有可用度和任务可靠度值下降，任务可靠性的值也会下降，假设为Kkx，如果用影响距离来表示可靠性影响，则可靠性对系统效能的影响亦即可靠性的变化为：

3　武器系统可靠性计算与分析

3.1任务可靠性计算

假设任务：主炮、副炮对海射击。参数假设：主炮、副炮系统已经工作过时间为3 h，相应的其他系统已工作时间均为10 h（其他系统可靠性值查阅《某型舰可靠性分配方法》获取）。射击时间主炮为30 min，副炮为3 min。可首先绘制任务分解图。

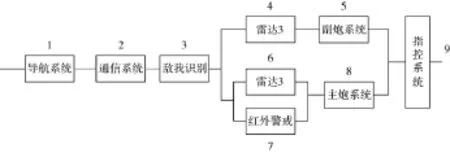
图3　对海射击任务分解

根据式（1）、式（6）和式（7）可以进行主副炮对海射击的任务可靠性计算，这里假设主副炮在对海射击任务中任务比率均为0.5。计算中时间取值，主炮为5 min一个步长，副炮为30 s一个步长。计算结果如图4所示。

3.2任务可靠性影响分析

根据式（8）分析和计算当随着任务时间变化，系统可靠性变化后对任务可靠性的影响，计算结果如图5。

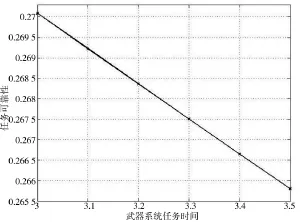
图4　对海射击任务可靠性

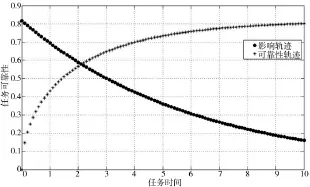
图5　可靠性影响分析

由图4、图5可以得到结论：①任务可靠性是单调指标，随着任务时间增长，呈现出“越来越小”的趋势；②任务可靠性对效能的影响也具有单调性，随着任务可靠性降低，影响越来越大，任务效能越来越低；③由于主副炮的可靠性较低，在完成对海射击任务时，任务可靠性不高；④在一个任务周期内，主副炮的可靠性降低，但是任务可靠性降低幅度较小。

3.3通道可靠性计算

仍然以主副炮为例进行通道可靠性计算。根据式（1）～式（3）计算通道可靠性值如表2。

表2　武器系统通道可靠性计算值

由表2可得到结论：①相同武器系统的通道中，系统数少的通道可靠性较高；②相同武器系统的通道中，同样数量系统的通道，系统可靠性高的通道其通道可靠性较高；③如果采用别的通道替换任务分解图3中的主副炮通道，对海射击任务可靠性将发生改变。

4　结束语

由上述计算和分析可以看出，系统可靠性不但决定了通道可靠性和任务可靠性的大小，通道结构和任务结构也是决定通道可靠性和任务可靠性的重要因素，三者相互联系并对效能产生影响。因此，在以完好性为中心的装备保障研究中，不仅要了解系统可靠性的概念，理解系统可靠性、通道可靠性和任务可靠性的关系及模型，而且还要深入分析其对效能产生影响的本质，为提高武器系统效能决策研究提供理论依据。

［1］李院生，时和平.装备战备完好性及其影响因素分析［J］.电子产品可靠性与环境试验，2007，25（1）：38-41.

［2］王春生，夏学知.舰载作战指挥系统可靠性模型分析［J］.舰船电子工程，2000（3）：40-42

［3］刘德生，郭静.基于探索性分析方法的导弹对抗作战效能评估［J］.微计算机信息，2010，26（9）：30-32.

［4］冯川，汪文峰，杨建军.使用可用度分配模型研究［J］.电子产品可靠性与环境试验，2009，26（6）：49-52.

Ship-board Weapon System Reliability Model and Exploratory Research

WANG Qin，HUANG Li-wei，SU Qi
（Dalian Naval Academy，Dalian 116018，China）

Based on the exploratory research method of model analysis，influence analysis and parameter discussion，This paper investigates the weapon system reliability from the three aspect of system reliability，mission reliability and chunnel reliability.And then，this paper presents the research result，which expounds the relationship of the three aspect and the influence to weapon system efficiency.All of this will offer the theory gist for the weapon system efficiency research.

weapon system reliability，series-parallel connection system，exploratory research

U462

A

1002-0640（2015）01-0067-03

2013-11-20

2014-01-09

王勤（1977-），男，湖北武穴人，硕士。研究方向：舰艇作战模型等。