车载雷达稳定转台伺服系统有限时间积分滑模控制
冯瑗瑗,华光辉
(1.中国船舶重工集团公司第七二四研究所,南京 211153;2.中国电力科学研究院,南京 210003)
车载雷达稳定转台伺服系统有限时间积分滑模控制
冯瑗瑗1,华光辉2
(1.中国船舶重工集团公司第七二四研究所,南京 211153;2.中国电力科学研究院,南京 210003)
摘要:应用有限时间稳定和积分滑模控制理论,提出了一种响应速度快、具备较强抗干扰能力的车载雷达稳定转台伺服系统新型控制方法。建立了被控对象和控制系统的四阶数学模型,基于MATLAB开展了计算机仿真实验,验证了有限时间积分滑模控制效果,为工程应用奠定了基础。
关键词:车载雷达;伺服控制系统;有限时间稳定;积分滑模;计算机仿真
0引言
车载雷达稳定转台是一个机械传动装置。它可以使安装在车辆上的雷达天线不受车辆运动的影响,在车辆出现倾斜或转向时,让天线始终保持某一个给定的方向和倾角,从而保持雷达的正常工作。稳定转台是车载雷达的重要组成部分,对于发现目标、跟踪目标以及测量目标的位置、速度等参数都起着重要作用。随着现代雷达技术的不断发展,车载雷达对稳定转台伺服控制系统也提出了越来越高的技术需求[1]。伺服控制除了常规的PID控制技术外,还有智能PID控制、智能控制、自适应控制、滑模控制等[2]。
滑模控制系统的动态性能主要取决于滑模面的选择。传统的滑模控制器设计的滑模面具有线性的形式,只能保证系统状态在滑模面上渐近收敛。为了改善系统的收敛特性和抗扰动性能,国内外学者结合有限时间控制理论提出了很多解决办法,使系统状态达到滑模面后可在有限时间内滑动到原点[3]。
文献[4]提出一种积分滑模控制方法,并通过仿真证明在伺服系统出现参数变化和外部干扰时,积分滑模控制系统有很高的动态性能和很好的鲁棒性。文献[5]指出对不确定和扰动的系统进行控制时,有限时间稳定系统与一般渐近收敛的无限时间稳定系统相比,在原点附近具有更快的收敛性,而且具有更好的鲁棒性和抗干扰能力。文献[6]从最优控制的角度设计了基于有限时间收敛的新型滑模控制器,可以使系统获得较好的鲁棒性。文献[7]设计了传统滑模变结构控制器,通过计算机仿真方式与经典PID控制方法进行了对比,证明了滑模控制的控制效果。
本文在传统滑模控制的基础上,根据有限时间控制理论和积分滑模控制,提出一种新的有限时间滑模控制器设计方法。它可以提高闭环系统状态在滑模面上的收敛速度,使稳定转台伺服系统快速收敛。
1被控对象的机理模型
1.1 伺服系统三质量数学模型
本文所研究的车载雷达为两轴稳定转台,雷达天线的目标给定角度通过方位控制通道和俯仰控制通道驱使雷达稳定转台在方位和俯仰两个自由度上旋转,共同作用使雷达天线指向预定方向。以方位控制为例,建立车载雷达稳定转台方位控制系统数学模型[7]。
为保证稳定转台的控制精度,在此对伺服系统建立三质量数学模型,即由包括电机、纯惯性负载以及连接二者的等效传递机构三部分组成,其数学模型如图1所示。
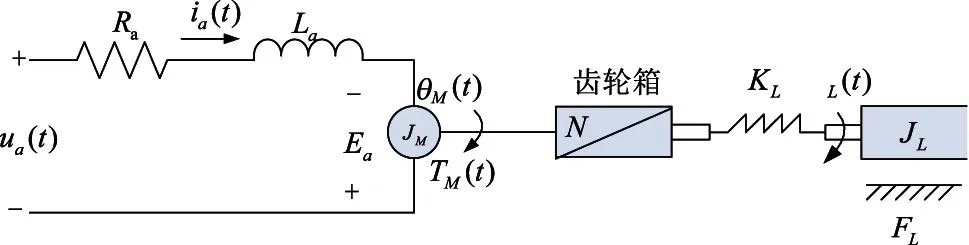
图1 电机通过弹性轴驱动负载的组合模型
然后可以列出方程:
(1)
(2)
TM=KTIa
(3)
(4)
(5)
(6)
式中,Ua是加在电机电枢两端电压,Ea是电机反电动势,Ia是电枢电流,Ra是电机的电枢电阻,La是电机的电枢电感,Km是电机反电动势系数,θM电机轴的角位移,TM是电机力矩,KT是电机力矩常数,JM是电机电枢转动惯量,T是弹性轴中的力矩(即作用于负载上的力矩),N是齿轮箱减速比,KL是弹性轴的刚性,θL是传动架的角位移,JL是负载惯量,FL是黏性摩擦常数。
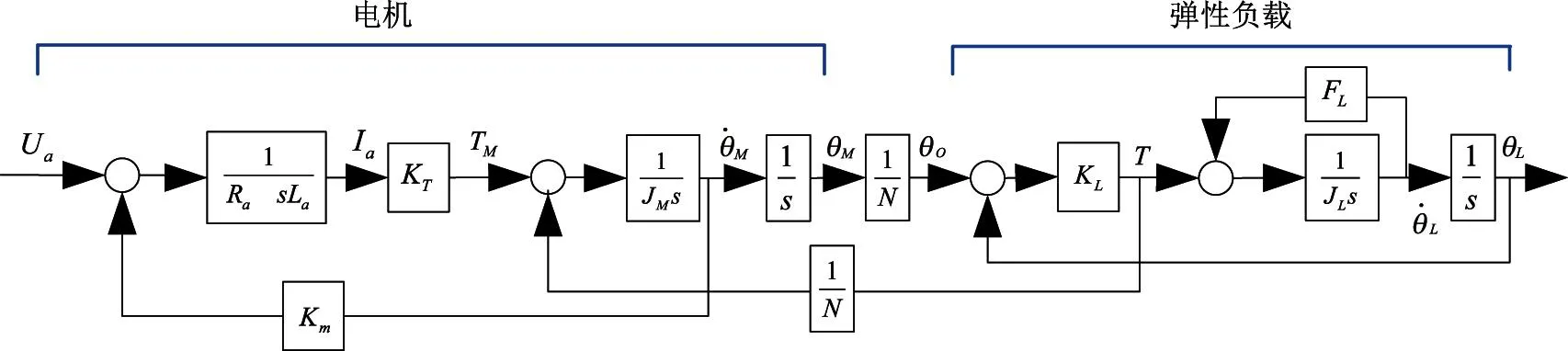
图2 系统模型的方框图
1.2 稳定转台伺服系统的摩擦模型
本文采用一种如图3所示的Stribeck摩擦模型。由于在不同的阶段物体接触面之间的相对运动速度也不一样,因此在稳态时摩擦力表现为物体相对速度的函数[8]。该模型给出了在不同摩擦阶段摩擦力与速度之间的关系。
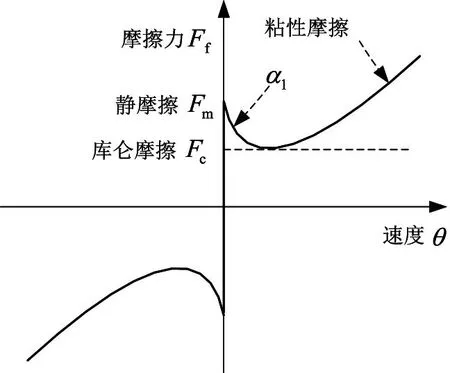
图3 Stribeck摩擦模型
(7)
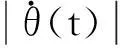
(8)
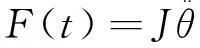
(9)
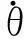
1.3 伺服系统PID控制
伺服控制常用的控制方法是PID控制,而且一般采用位置和速度双闭环控制。经过控制参数寻优,可以取得较理想的阶跃响应曲线如图4所示。
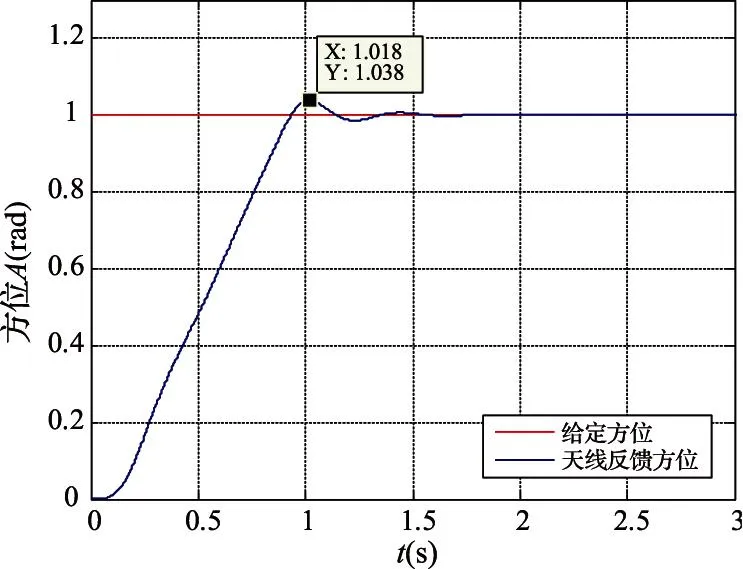
图4 PID控制位置阶跃响应曲线
可以看出,在对被控对象进行精确建模的情况下,传统PID控制能够取得较为理想的控制效果。但是,当系统参数发生变化或者外部出现干扰时,其超调量、过渡时间等性能指标会显著下降,详细研究内容见参考文献[7]。
2有限时间稳定性相关理论
2.1 有限时间稳定性定义
定义1[9]考虑如下系统:
(10)
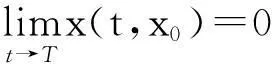
2.2 积分链系统有限时间收敛算法
引理1[9]假设存在φ1,φ2,…,φn>0使得多项式sn+φnsn-1+…+φ2s+φ1是Hurwitz的,考虑如下系统:
(11)
存在μ∈(0,1),使得∀α∈(1-μ,1),对于上述系统控制器设计如下:
(12)
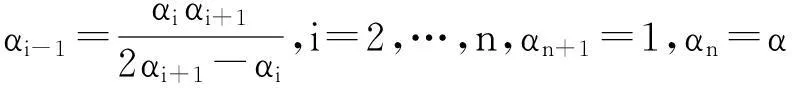
有限时间控制器中带有分数幂项。这一特点使得有限时间闭环控制系统与非有限时间闭环控制系统相比,前者具有更好的鲁棒性和抗扰动性能[5]。
2.3 有限时间积分滑模面设计
本文定义积分滑模面如下[10-11]:
(13)
其中控制率u已在引理1中给出。t0是初始时间,容易推出t=t0时,s(t0)=0。因此,系统从初始时刻起就在滑模面上。
3伺服系统有限时间积分滑模控制器设计
设
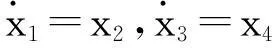
(14)
其中
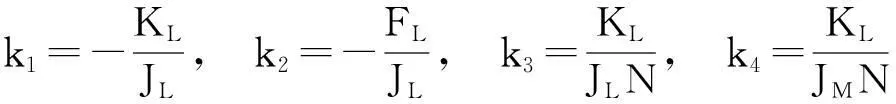
此系统为单输入系统,其系数矩阵的秩等于4,属于非奇异矩阵,系统完全能控。
为了构造滑模函数,设
(15)
式中
(16)
(17)
(18)
(19)
被控对象阶数n=4,设α=4/5,则滑模面函数为
(20)
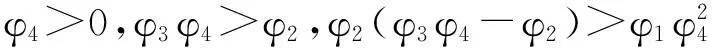
滑模面函数的导数为
(21)
其中
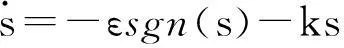
(23)
4有限时间积分滑模控制器仿真实验
针对前文所给出的车载雷达稳定转台伺服系统被控对象参数,根据有限时间积分滑模控制器设计方法,基于MATLAB仿真开展相关实验,验证控制算法的有效性和优越性[12-15]。
取φ1=20 000,φ2=16 000,φ3=4 000,φ4=300,k=100,ε=20,天线反馈方位在有限时间内跟踪给定方位,而且能够较好地跟踪给定值,如图5所示。
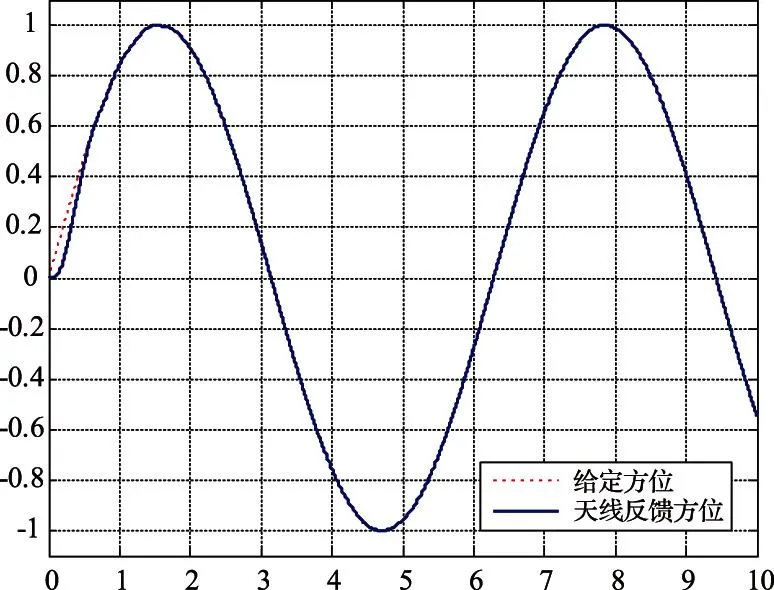
图5 位置给定与天线位置跟踪曲线
此时控制器u的输出如图6所示。可见除了在启动阶段有几次振荡之外,控制量输出已经基本没有抖振现象,说明该控制器对系统抖振也具有较强的抑制作用。
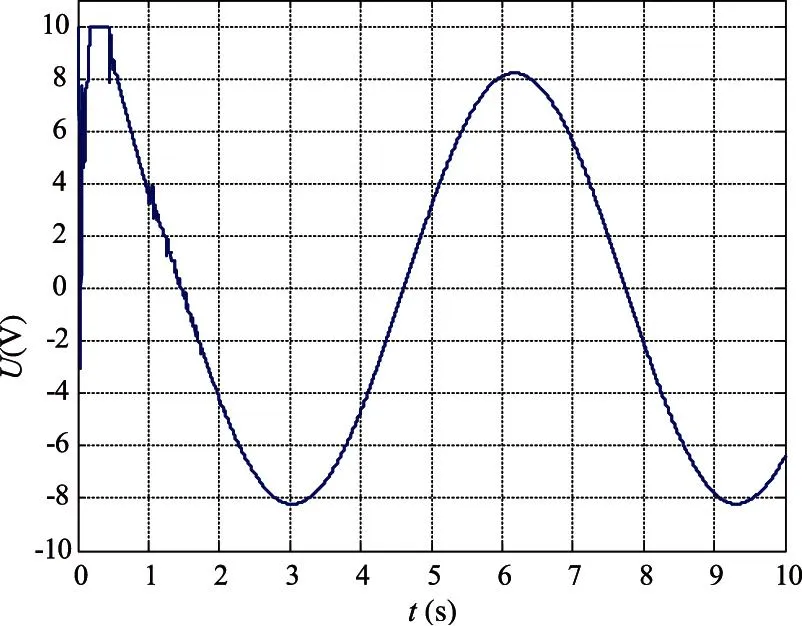
图6 控制量输出曲线
方位给定与天线反馈位置之差e的曲线如图7所示。可见时间在1s时,误差收敛到0,表明系统能够在1s的有限时间内有效地跟踪参考曲线。
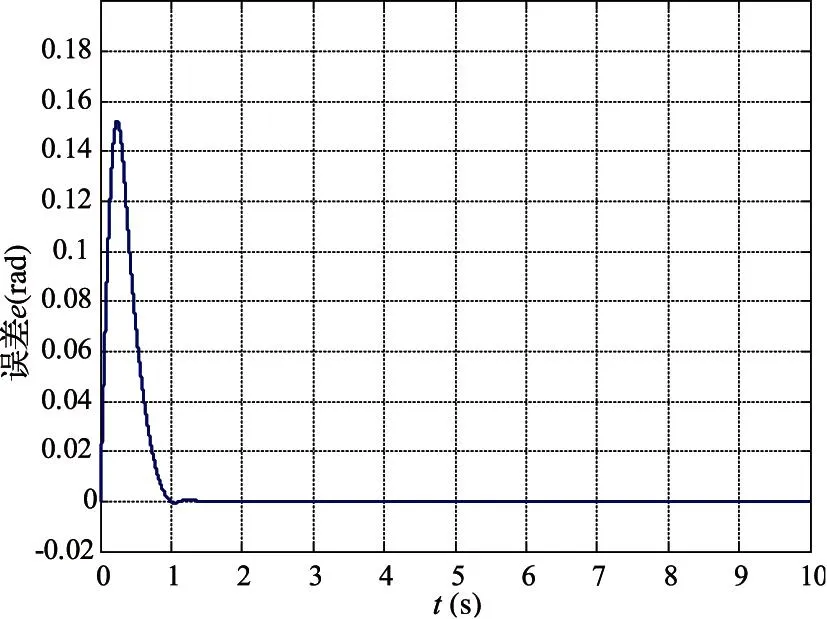
图7 位置跟踪误差曲线
开展伺服系统内部参数变化对比试验,负载惯量由原先的150kg·m2变为250 kg·m2,变化前后的阶跃响应曲线如图8所示。可见两条曲线相差很少,基本保持一致。
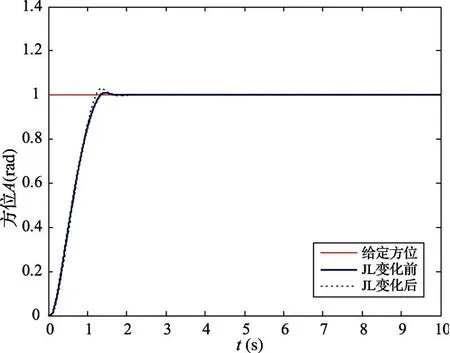
图8 负载惯量发生变化时方位跟踪曲线
当粘性摩擦系数FL发生了变化,假设由原来的1500N·m·s/rad增大为3000N·m·s/rad,变化前后的阶跃响应曲线如图9所示,可见变化后超调量有所增加,但是基本保持一致。
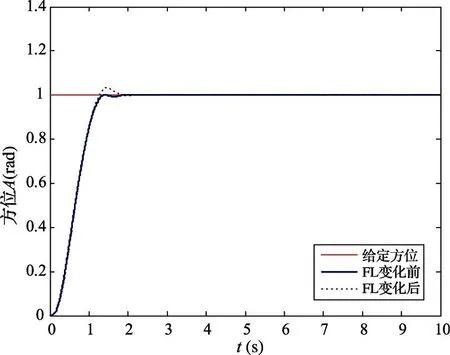
图9 粘性摩擦系数发生变化时方位跟踪曲线
利用Stribeck摩擦模型来模拟控制参数时变的伺服控制系统,完成车载雷达稳定转台方位阶跃试验,曲线如图10所示。可见针对摩擦系数时变系统,所设计控制系统是收敛的,而且动态、静态控制效果也同样满足设计要求。
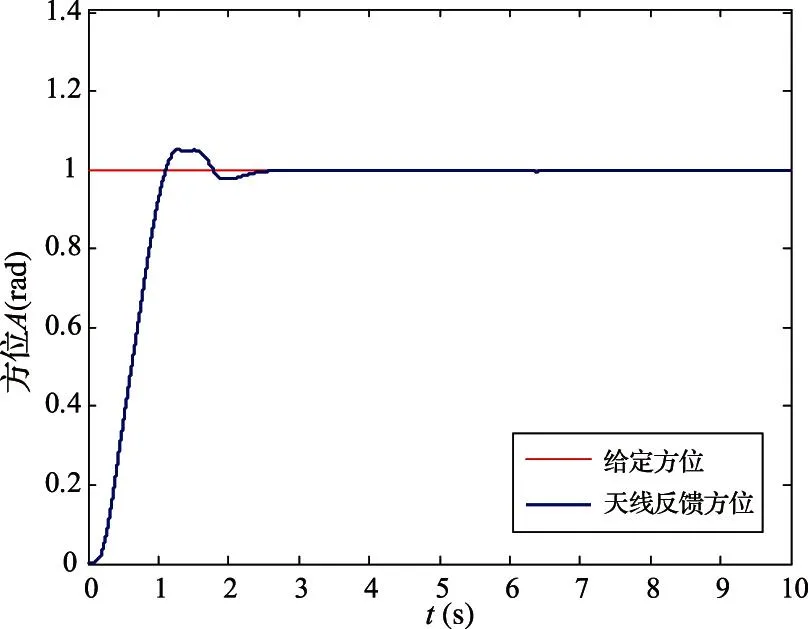
图10 摩擦系数时变系统方位跟踪曲线
当在负载力矩处叠加TO=-1000 N·m的持续外部干扰时,通过仿真试验可以得到如图11的对比曲线。可见增加外部干扰后超调量有所增加,但系统能够在有限时间内快速稳定。
在实际工作中,两轴稳定转台由于天线姿态变换、机械连接、加工工艺、信号不同步等因素,方位和俯仰两轴之间存在着交叉耦合[16-17]。图12在正弦给定的基础上叠加方波信号,模拟方位控制闭环做扇扫控制的同时出现俯仰通道的耦合信息的情况,雷达天线方位能够快速跟踪给定信号,具有较好的解耦控制能力。
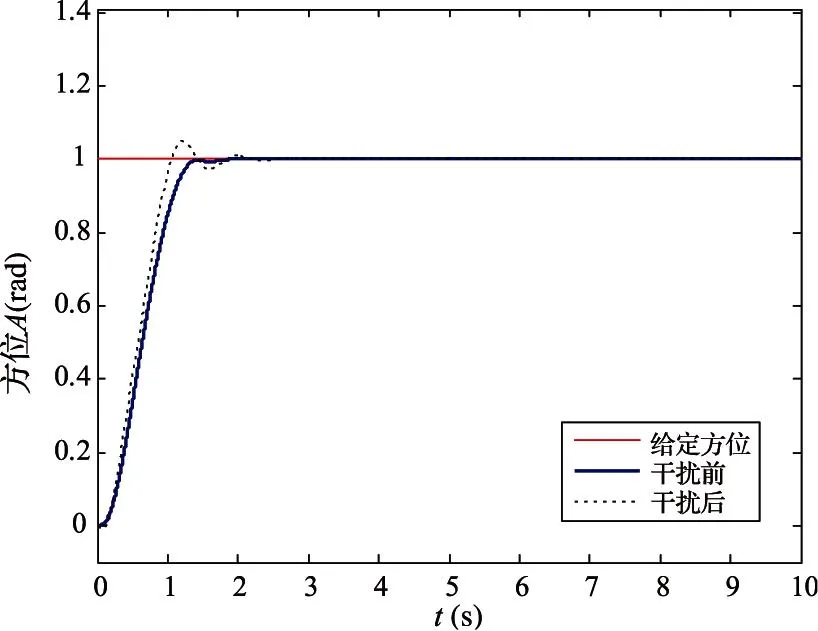
图11 系统出现外部干扰时方位跟踪曲线
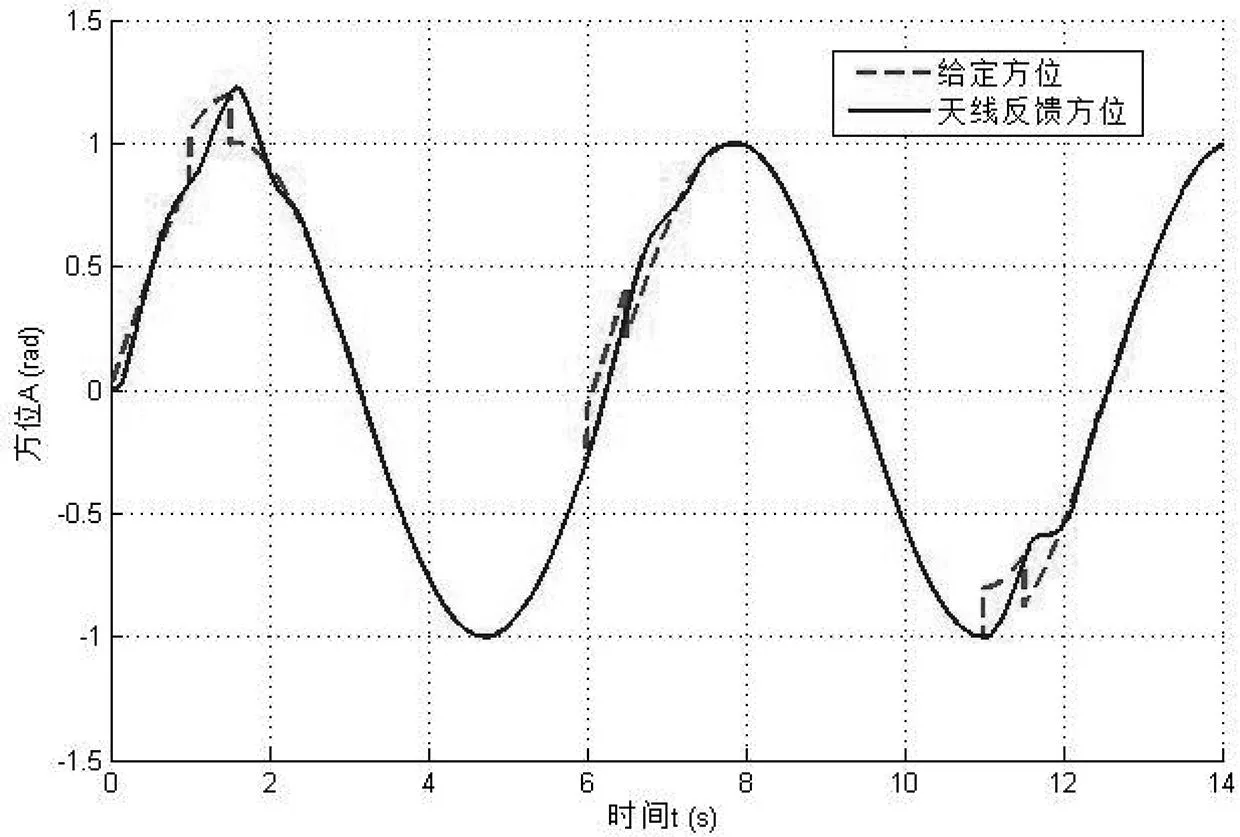
图12 两轴交叉耦合时方位跟踪曲线
通过以上计算机仿真实验可以得知,本文设计的有限时间积分滑模控制器能够有效抑制系统抖振,而且在出现参数变化、外部扰动、交叉耦合时依然具有良好的鲁棒性,控制效果良好。
5结束语
本文将伺服控制单元和天线负载合在一起看作被控对象,建立了车载雷达稳定转台的三质量数学模型,提出了控制对象的四阶传递函数,并建立了状态方程。根据有限时间稳定和积分滑模控制理论,给出了一种新的有限时间收敛的滑模控制器设计方法,并结合Stribeck摩擦模型对伺服控制方法进行了深入研究。通过MATLAB仿真证明,相比传统的PID控制器,本文设计的有限时间积分滑模控制器具有更强的鲁棒性,能够有效提高收敛速度,保证系统快速响应。
参考文献:
[1]刘世挺.雷达伺服控制技术的新发展[J].火控雷达技术,2002,27(1): 33-35.
[2]董彩云.基于滑模变结构控制的电液伺服系统及实验研究[D].秦皇岛: 燕山大学,2007.
[3]丁世宏,李世华.有限时间控制问题综述[J].控制与决策,2011,26(2): 161-169.
[4]汤青波,张国新,何学文.电液伺服系统的积分滑模控制[J].机床与液压,2011,39(9): 48-50.
[5]刘慧贤,丁世宏,李世华,等.永磁同步电机位置伺服系统的有限时间控制[J].电机与控制学报,2009,13(3): 424-430.
[6]SalahLaghrouche,FranckPlestan,AlainGlumineau.Higherorderslidingmodecontrolbasedonintegralslidingmode[J].Automatic,2007,43(3): 531-537.
[7]冯瑗瑗,丁锋.车载雷达稳定转台伺服控制系统仿真研究[J].机电信息,2014,6: 144-146
[8]张国柱,陈杰,李志平.直线电机伺服系统的自适应模糊摩擦补偿[J].电机与控制学报,2009,13(1): 154-160.
[9]刘慧贤,王钊,李世华.永磁同步电机位置伺服系统的有限时间位置控制[J].系统科学与数学,2010,30(6): 721-732.
[10]Zong Q,Zhao Z S,Zhang J.Higher order sliding mode control with self-tuning law based on integral sliding mode[J].IET Control Theory and Applications,2010,4(7): 1282-1289.
[11]赵占山,张静,孙连坤,等.有限时间收敛的滑模自适应控制器设计[J].山东大学学报,2012,42(4): 74-78.
[12]邹云飞,刘金琨,王宗学.转台伺服系统滑模变结构控制器的设计与仿真研究[J].计算机仿真,2002,19(2):74-76.
[13]刘金琨.滑模变结构控制MATLAB仿真(第2版)[M].北京: 清华大学出版社,2012.
[14]陈志梅,王贞艳,张井岗.滑模变结构控制理论及应用[M].北京: 电子工业出版社,2012.
[15]陈杰,李志平,张国柱.不确定非线性系统的高阶滑模控制器设计[J].控制理论与应用,2010,27(5): 563-569.
[16]鲍文亮,黄显林,卢鸿谦.多框架光电平台动力学建模及耦合分析[J].哈尔滨工程大学学报,2009,30(8): 893-896
[17]王俊峰,左增宏.单通道单脉冲自跟踪系统交叉耦合分析[J].飞行器测控学报,2009,28(3): 30-33
Finite-time integral sliding mode control of servo system for
vehicle-borne radar stabilizing rotary platform
FENG Yuan-yuan1, HUA Guang-hui2
(1. No.724 Research Institute of CSIC, Nanjing 211153;
2. China Electric Power Research Institute, Nanjing 210003)
Abstract:A novel control method of the servo system for the vehicle-borne radar stabilizing rotary platform with fast response and strong anti-jamming capability is proposed, applying the theory of the finite-time stability and the integral sliding mode (ISM) control. A four-order mathematical model of the controlled object and the control system is established, and the computer simulation tests are carried out based on the MATLAB, verifying the effect of the finite-time ISM control, and laying the foundation of engineering application.
Keywords:vehicle-borne radar; servo control system; finite-time stability; ISM; computer simulation
中图分类号:TN820.3
文献标志码:A
文章编号:1009-0401(2015)04-0054-06
作者简介:冯瑗瑗(1984-),女,工程师,研究方向:雷达伺服系统控制;华光辉(1983-),男,高级工程师,研究方向:新能源发电技术、电机控制技术。
收稿日期:2015-07-20;修回日期:2015-07-25

