中浓度纸浆流态化特征

叶道星，李 红，邹晨海，刘振超

(江苏大学国家水泵及系统工程技术研究中心，江苏镇江 212013)

中浓度制浆技术克服了低浓度纸浆制浆过程所存在的效率低、耗能和污染环境等缺点，是高效、低耗和少污染的制浆技术.中浓度纸浆悬浮液为一种气液固三相的非牛顿流体［1-4］，其物理特性十分复杂.目前国内外研究主要针对低浓度的纸浆，对中浓度纸浆的研究还很缺乏，纸浆的流态化是实现中浓度制浆过程的先决条件，因此对中浓度纸浆流态化的研究具有非常重要的意义.

中浓度纸浆作为伪塑性非牛顿流体，当施加的剪切应力超过某一极限值时，由于纸浆纤维网络发生断裂，因而纸浆开始表现为流态化状态.R.J.Kerekes等［5-7］研究发现由于纸浆絮凝物和纤维的表观屈服应力存在着很大的差异，所以造成纸浆的流态化发生在纸浆絮凝物和纤维2个水平点上.絮凝物水平的流态化是实现纸浆抽送的充分条件，但是纤维水平的流态化在一些流程中只是必要条件.J.Gullichsen等［8］在一个给定尺寸的容器中通过转矩产生湍流动能从而间接地获得纸浆流态化的表观屈服应力值.D.Wahren等［9］量化了纸浆流态化发生时的能量耗散，但是由于容器尺寸的不同，造成能量的耗散有着巨大的梯度差异，为此C.P.J.Bennington等［6］建立了能量耗散与流态化设备的几何尺寸的函数关系，研究发现纤维水平的流态化发生在旋转叶片的间隙处，大多数絮凝物水平的流态化发生在远离转子的区域.V.B.Rewatkar等［10］对中低浓纸浆气液混合流动特性进行了分析研究，得出部分种类的纸浆在搅拌作用下的功率耗散和功率准数等数据.陈奇峰等［11］以气-液两相流欧拉模型及基于雷诺时均法的混合湍流模型对10%纸浆悬浮液的流态化过程进行了CFD模拟，并以温度的变化分布来反映湍流均匀度，结果与试验吻合较好.

J.Gullichsen等［8］确定了旋转设备中纸浆流态化的必要条件，并在此基础上设计了可以抽送质量分数为15%的纸浆悬浮液的离心泵.在后来的研究中C.P.J.Bennington等［12］对纸浆的流态化进行了更多的深入研究.L.L.Andrew［13］提出了一种设计中浓纸浆输送装置的方法，并重点研究得出了中浓纸浆输送管路损失的曲线.陈克复［14］对木浆和草浆做了部分研究，建立了临界剪切应力与浓度的关系，但主要针对质量分数在10%左右，缺少对更高浓度的研究.

上述研究主要对部分中低浓度纸浆的功率数，表观屈服应力以及流态化的条件进行了分析，然而缺乏中浓度纸浆功率数、表观屈服应力、临界剪切应力与旋转速度和纸浆浓度之间关系的研究.因此笔者在中浓度纸浆流态化过程中，建立功率数和剪切应力与转速的关系以及表观屈服应力和临界剪切应力与浓度的数学模型.研究中浓度纸浆在不同剪切力下的流动特征，找到中浓度纸浆在流态化过程中的变化规律，实现中浓度纸浆悬浮液的流态化，从而达到泵送中浓度纸浆的目的.

1 试验装置

为了测量中浓度纸浆在搅拌叶轮不同转速下所受到的剪切应力、功率数等参数，设计了一套纸浆流变测试装置，如图1所示.

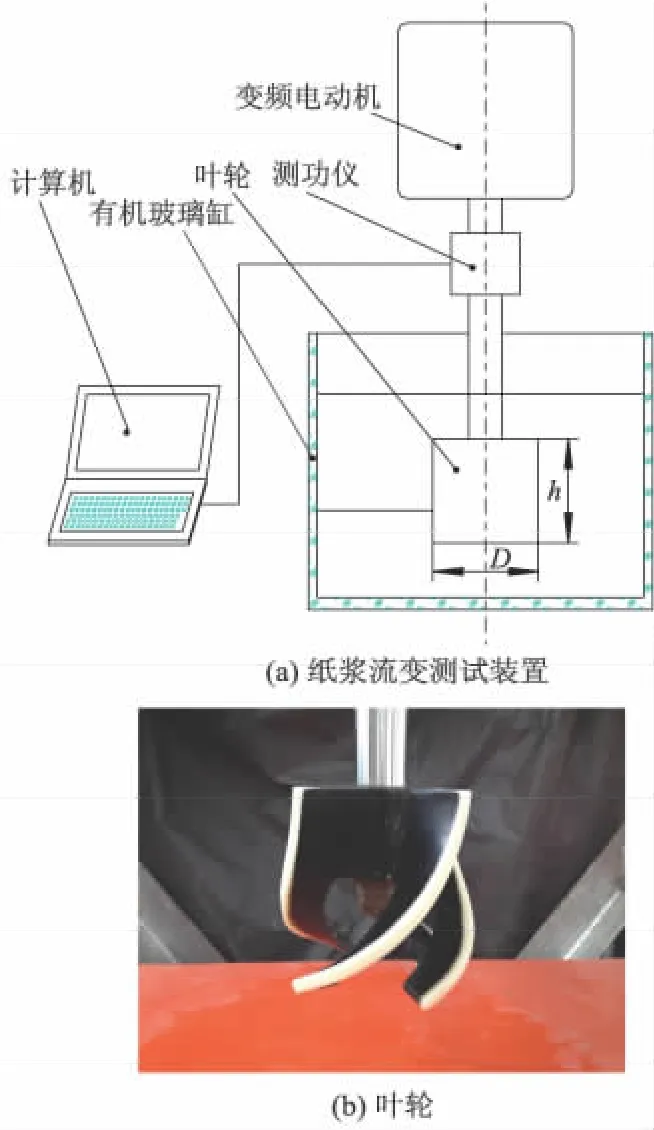
图1 纸浆流变测试装置和叶轮

该装置采用15 kW变频电动机作为搅拌叶轮的驱动动力，可以轻松实现叶轮旋转速度的大幅度调节.转速、转矩和功率等数据由转矩转速传感器将其转换为电信号，输入计算机.叶轮的直径D=150 mm，叶片高度h=160 mm.

2 中浓度纸浆理论分析

对旋转剪切室进行受力分析，如图2所示.

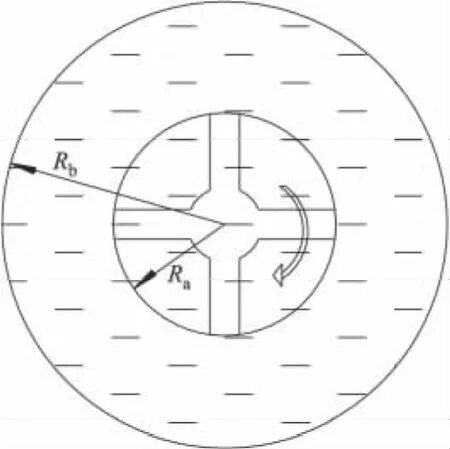
图2 流动剪切示意图

当纸浆做恒定的旋转流动时，其加速度为0，所受到的合力矩为0，剪切区域内纸浆的剪切力矩相等:

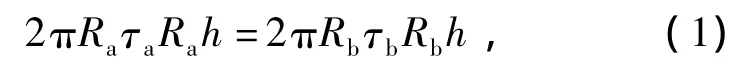
式中:Ra为叶轮的半径，m;Rb为剪切室的内径，m;τa，τb为所对应半径的剪切应力，Pa.

从图2可以看出:纸浆在半径为Ra时所受到的剪切力最大，进而得到在叶轮外径圆柱面上纸浆受到叶轮的剪切力矩为

式中:R为叶轮外径，m;τ为纸浆所受到的剪切应力，Pa.

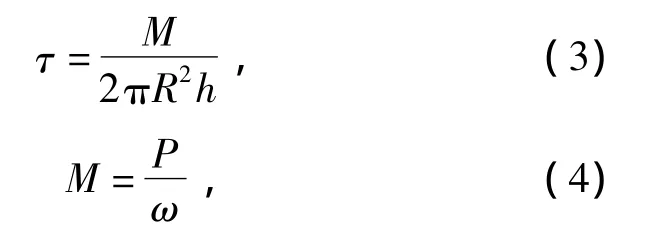
式中:P为轴功率，W;ω为旋转角速度，rad·s-1.

为了判断中浓度纸浆的流动状态，采用功率数作为判断的依据.功率数为

式中:ρ为纸浆密度，kg·m-3;n为转速，r·min-1.

3 试验结果及分析

3.1 中浓度纸浆密度和浓度的测试

采用烘干称重法，测量了纸浆的质量分数:

采用体积法测量中浓度纸浆的密度，所使用的精密电子天平型号为RS-232，其精度为0.005 g.量筒的量程为250 mL.其密度按照式(7)确定，即3次密度测量值的平均值作为试验测量值，其密度如表1所示.

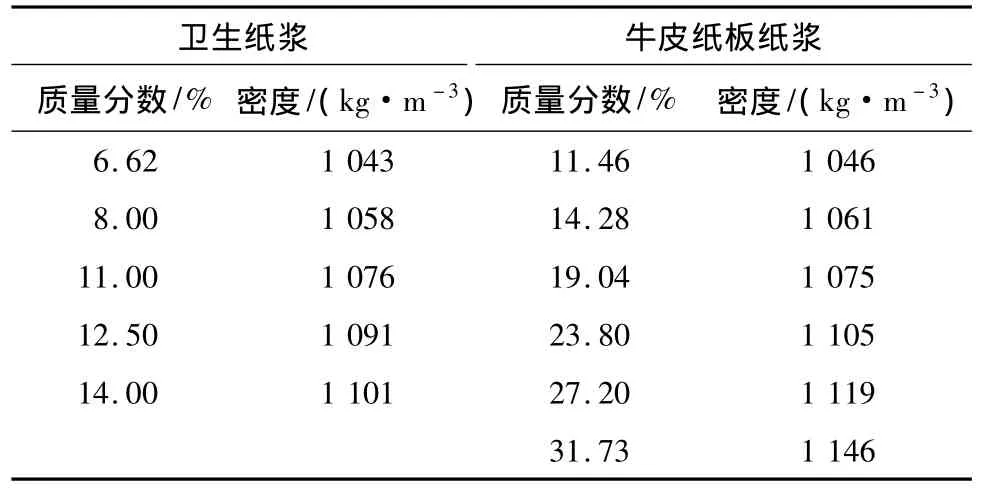
表1 中浓度纸浆的密度

根据试验所测得的密度值，发现纸浆的密度随着纸浆的质量分数呈线性变化，得到密度与质量分数之间的关系为

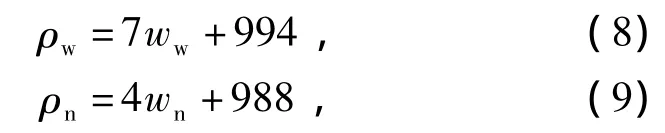
式中:ρw为卫生纸浆密度;ww为卫生纸纸浆的质量分数;ρn为牛皮纸板纸浆密度;wn为牛皮纸板纸浆的质量分数.

3.2 中浓度纸浆的功率数的变化规律

卫生纸浆功率数与转速之间的关系如图3所示，牛皮纸板纸浆功率数与转速之间的关系如图4所示.

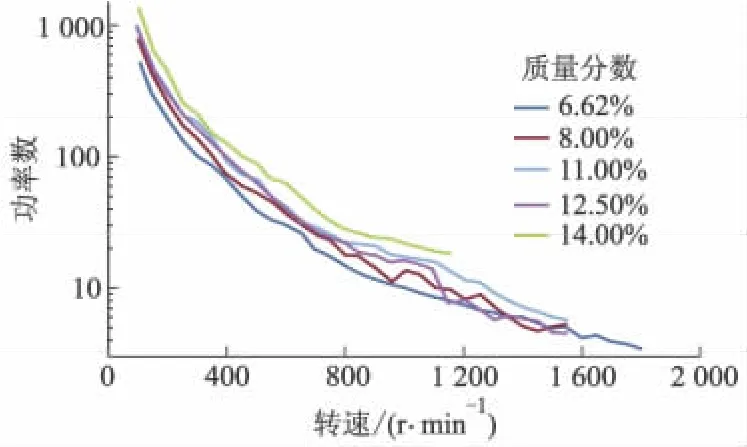
图3 卫生纸浆的功率数

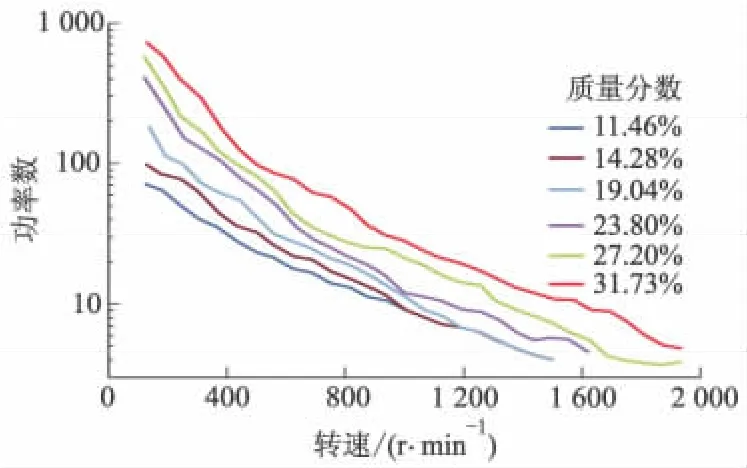
图4 牛皮纸板纸浆的功率数

从图3，4可以看出:在2种纸浆中，相同转速下，功率数随着纸浆质量分数的增加而不断升高.随着转速的增加，纸浆的功率数随之下降，当转速达到1 000 r·min-1左右，除了质量分数为14.00%的卫生纸浆和31.73%牛皮纸板纸浆外，其余的纸浆功率数都低于10，变化波动较小，因此认为此时的纸浆已经达到湍流的状态.这与王凯等［15-16］的研究结果相吻合.

3.3 中浓度纸浆的表观屈服应力和临界剪切应力

在如图1所示的试验装置上，对中浓度的卫生纸浆和牛皮纸板纸浆进行了剪切应力及转速的测量，采用5次方数学模型进行了拟合:

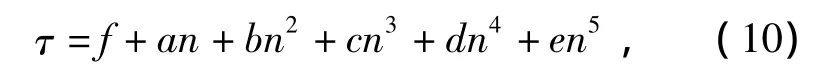
式中a，b，c，d，e，f分别为不同系数.

卫生纸浆和牛皮纸板纸浆在不同质量分数下所对应的拟合公式系数分别如表2，3所示，可以发现在不同质量分数下，模型的系数相差很大.使用模型预测时，应注意纸浆类型及质量分数.

表2 卫生纸浆剪切应力数学模型系数

表3 牛皮纸板纸浆剪切应力数学模型系数

卫生纸浆和牛皮纸板纸浆剪切应力随转速的变化分别如图5，6所示.

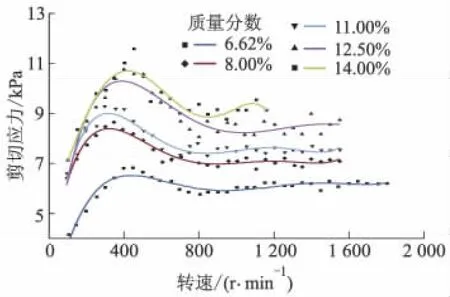
图5 卫生纸浆的剪切应力

图6 牛皮纸板纸浆的剪切应力

从图5，6可以看出:随着转速的增加，纸浆的剪切应力先增加后减小，最后呈现为较平稳的特征，对应纸浆流动状态的启动、稳定和流态化3个阶段;在试验装置中纸浆的流动方向由轴向运动转换为径向运动，随着纸浆质量分数的增加，剪切应力随之增加;在相同转速和质量分数下卫生纸浆的剪切应力比牛皮纸板纸浆的剪切应力大，可以得出卫生纸浆更需要足够大的剪切应力才能使其流态化.剪切应力的最大值称为纸浆的表观屈服应力，纸浆开始表现为流态化状态时的剪切应力称为临界剪切应力.根据试验所得数据可以得到不同质量分数下纸浆的表观屈服应力和临界剪切应力值.卫生纸浆和牛皮纸板纸浆的表观屈服应力和临界剪切应力分别如表4，5 所示.

表4 卫生纸浆的表观屈服应力和临界剪切应力

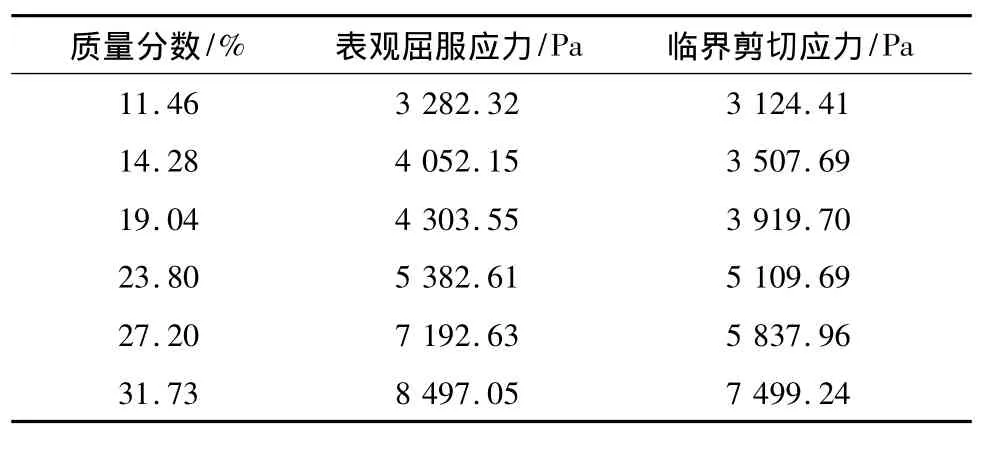
表5 牛皮纸板纸浆的表观屈服应力和临界剪切应力

从表4，5可以看出:中浓度纸浆的表观屈服应力和临界剪切应力随着质量分数的增加都同时增加.对试验数据进行回归处理，发现纸浆的表观屈服应力和临界剪切应力与纸浆质量分数之间成3次方的关系.卫生纸浆的表观屈服应力为

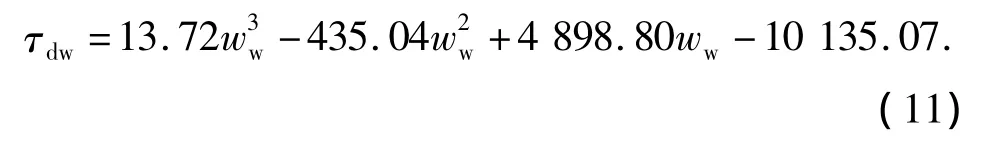
卫生纸浆的临界剪切应力为

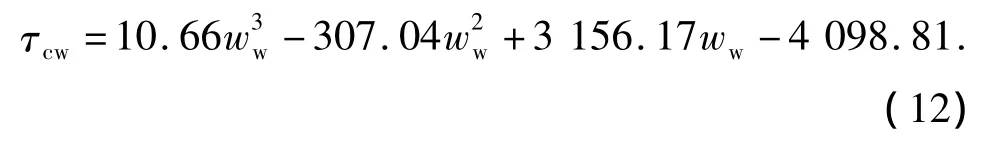
牛皮纸板纸浆的表观屈服应力为

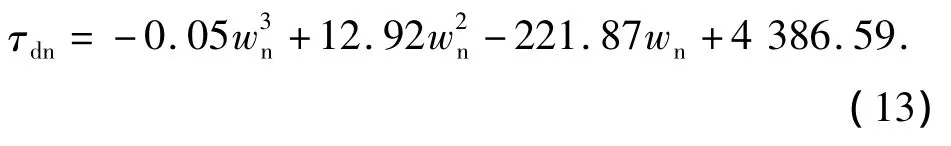
卫生纸浆的临界剪切应力为

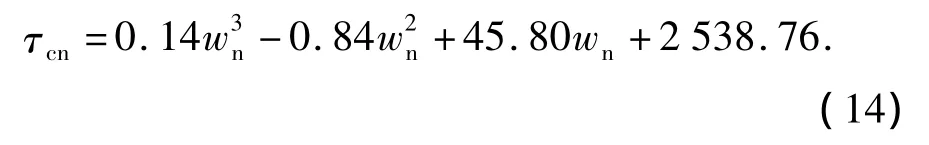
4 结论

1)试验测量了2种中浓度纸浆的流动性，得到了中浓度纸浆的密度与质量分数之间的关系.根据试验数据，建立了中浓度纸浆的剪切应力与转速的数学模型，发现采用5次方的剪切应力数学模型能够反映出中浓度纸浆在受到旋转剪切时所表现出的规律:随着转速的增加，剪切应力先增加后减小，最后达到平稳的过程，分别对应纸浆流动状态的启动、稳定和湍流3个阶段.

2)根据试验所得的数据与剪切应力数学模型，找到了中浓度纸浆的表观屈服应力，同时判断出了纸浆湍流化时所需要的临界剪切应力.建立了中浓度纸浆的表观屈服应力和临界剪切应力与纸浆质量分数的关系模型.通过试验分析，得到功率数随着转速的增加不断下降直到一个稳定值，同时随着纸浆质量分数的增加，功率数增加.

References)

［1］Mason S G.The flocculation of pulp suspensions and the formation of paper［J］.Tappi Journal，1990，33:440-444.

［2］Duffy G G.The significance of mechanistic-based models in fiber suspension flow ［J］.Nord Pulp Pap Res J，2003，18:74-80.

［3］Ma X D，Li Z F，Yu H，et al.Experimental study on a medium consistency pump ［J］.Journal of Fluids Engineering，2013，135(10):104503-1-5.

［4］Ma X D，Wu D Z，Huang D S，et al.CFD analysis on a turbulence generator of medium consistency pump［J］.Materials Science and Engineering，2013，52(3):257-260.

［5］Kerekes R J.Pulp flocculation in decaying turbulence:a literature review ［J］.Journal of Pulp and Paper Science，1983，9(3):86-91.

［6］Bennington C P J，Kerekes R J，Grace J R.Motion of pulp fibre suspensions in rotary devices［J］.Canadian Journal of Chemical Engineering，1991，69(1):251-258.

［7］Hietaniemi J，Gullichsen J.Flow properties of medium consistency fibre suspensions［J］.Journal of Pulp and Paper Science，1996，22(12):469-474.

［8］Gullichsen J，Harkonen E.Medium consistency technology II:storage dischargers and centrifugal pumps［J］.Tappi Journal，1981，64(6):69-72.

［9］Wahren D.Fiber network structures in papermaking operations［C］∥Proceedings of the Institute of Paper Chemistry Symposium on Paper Science and Technology，the Cutting Edge，1979:112-129.

［10］Rewatkar V B，Bennington C P J.Gas-liquid mass transfer in low-and medium-consistency pulp suspensions［J］.The Canadian Journal of Chemical Engineering，2000，78:504-516.

［11］陈奇峰，陈广学，陈克复.中浓纸浆悬浮液的流态化研究及CFD模拟［J］.华南理工大学学报:自然科学版，2009，37(3):81-84.

Chen Qifeng，Chen Guangxue，Chen Kefu.Fluidization investigation and CFD simulation of medium-consistency pulp suspensions［J］.Journal of South China University of Technology:Natural Science Edition，2009，37(3):81-84.(in Chinese)

［12］Bennington C P J，Kerekes R J.Power requirements for pulp suspension fluidization ［J］.Tappi Journal，1996，79(2):253-258.

［13］Andrew L L.The right way to design medium consistency pulp systems ［J］.Engineering Conference，1998:1093-1104.

［14］陈克复.中高浓制浆技术与装置［M］.广州:华南理工大学出版社，1994.

［15］王 凯，虞 军.搅拌设备［M］.北京:化学工业出版社，2003

［16］Ein-Mozaffari F，Bennington C P J，Dumont G A.Suspension yield stress and the dynamic response of agitated pulp chests［J］.Chemical Engineering Science，2005，60(8/9):2399-2408.