基于遗传小波神经网络的海杂波预测
徐婷
(江苏科技大学 电子信息学院,江苏 镇江 212003)
基于遗传小波神经网络的海杂波预测
徐婷
(江苏科技大学 电子信息学院,江苏 镇江 212003)
根据相空间重构理论,提出了一种基于遗传小波神经网络(GA-WNN)的混沌时间序列预测方法。根据takens理论,计算出相空间重构所需延迟时间和嵌入维数。采用小波神经网络的构造和算法,将遗传算法用于网络参数优化,为混沌时间序列预测提供可靠依据。为验证模型的可靠性,使用IPIX雷达数据进行多步预测,仿真结果表明这个确定性的模型可以根据海杂波已知数据预测未来值的变化。与传统神经网络预测相比,遗传小波神经网络预测方法的拟合精度和预测精度更好。
海杂波;相空间重构;小波神经网络;遗传算法
长期以来人们把海杂波常被视为单一随机过程[1],如经典的对数-正态分布、威布尔分布和复合k分布等。但在一定程度上海杂波的内在特性并非如此。基于统计规律下的海杂波模型,仅能从数据上进行拟合,但不能对海杂波的演变过程和产生机理做出合理的解释。20世纪末,Simon Haykin等人先后对海杂波进行了动态特性的试验,并对混沌动力学以及混沌吸引子进行研究,提出了海杂波的动力学预测模型,内在的解释了海杂波的混沌动力学机制。
根据Simon Haykin的观点,海杂波建模问题,最终可以转化为寻求预测方程的问题。本文的理论意义在于深入揭示海杂波的内在特性,从相空间重构理论出发,利用遗传小波神经网络为工具,阐述了时间序列的预测方法。通过雷达实测数据的实验仿真,验证了将神经网络[2]引入到混沌时间序列的预测具有一定可行性,得出了海杂波具有短期可预测性的结论。
1 相空间重构理论
相空间重构又称动力系统重建,系统任一分量的演化都是由与之相互作用的其他分量决定的,因此这些相关分量的信息都隐含在其分量的发展过程中。这样我们就可以从海杂波时间序列中提取和恢复出系统真正的规律。Packard建议用原系统时间变量的延迟坐标来重构相空间,而根据Takens[3]嵌入定理,证明了当嵌入维数m≥2d+1,可以将整个嵌入维空间的轨迹恢复出来。Takens定理为混沌预测提供了坚实的理论基础。
Takens定理:M是d维流形,φ:M→M,φ是一个光滑的微分同胚,y有二阶连续导数,Φ(φ,y):M→R2d+1,其中
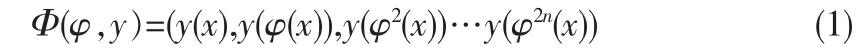
则是M到R的一个嵌入。
事实上Takens嵌入定理只适用于无噪声且无限长序列,因此嵌入定理仅为相空间重构提供了数学理论依据,并不能运用于实际应用中。假设M为一个d维的紧致流形,定义在M上的混沌系统可用下式等价:

对于一个混沌系统,若其初始状态为x(0),便可得到一系列状态点x(k),其中x(k)满足{x(k)=Φk(x(0)),k=1,2…}。对于杂波时间序列,若存在非线性函数f满足{y(n)=f(x)(n),n=0,1,2…},当嵌入维m≥2d+1时,映射Φ:M→M定义了和Φ:M→R相同的系统,于是可以通过相空间重构得到海杂波动力学系统的轨迹,相空间上的点可定义为
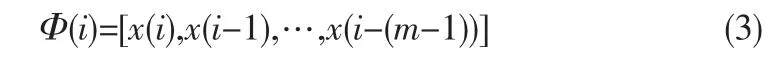
由映射Φ定义的系统可以用微分方程描述,可以得到Φ(i+1)=Ψ(Φ(i-1)),因此存在函数f使得
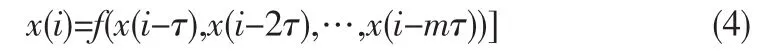
2 混沌参数的确定方法
在Takens定理中,只要数据是无限长且不存在噪声,那么延迟时间τ和嵌入维数m的任何选都是可以接受的,然而在实际测量中得到的海杂波序列,都是长度有限且包含环境噪声,因此参数的选取对重构质量造成影响。
2.1 延迟时间τ的确定
延迟时间τ若太小,将造成相空间矢量的相邻分量过于接近无法区分,从而无法提供独立的坐标分量;但若取得太大,则两坐标在统计意义上又完全独立,导致混沌吸引子失去相关性。本文采用互信息法计算延迟时间τ,表达式如下:

其中pi为xt在第i个时间间隔中的概率;pi,j(r)为点xt在t时刻落入第i个时间间隔和t+τ时刻落入第j个时间间隔的联合概率。M的大小描述了已知x(t)的情况下,x(t+τ)的确定性。为了简化计算,重构时选用M的第一个极小值作为延迟时间参数τ。
2.2 嵌入维数m的确定
关于嵌入维数的选取,伪邻近点法(FNN)是较常使用的方法。混沌时间序列呈现出无规律的原因,在于高维相空间中并不相邻的两点在一维空间轴上具有相同投影,即伪邻近点m。而随着嵌入维数m的增大,混沌吸引子逐渐打开,伪邻近点也会被剔除,从而将混沌运动的轨迹得到恢复,这就是FNN法主要思想。但是FNN算法存在对噪声敏感、主观选择性强等缺点,因此本文采用Cao Liangyue[4]提出改进的FNN算法(Cao法),该方法具有以下优点:1)除延迟时间外不包含其他主观参数;2)对数据长度依赖性不强,使用较小数据量就可以求得。
Cao算法主要引入了E1(m)和E2(m)两个变量。对于时间序列x1,x2,…,xN,当延迟时间为τ,嵌入维数为m时,空间第i个向量Yi(m)及其最邻近点YiNN(m)分别为:
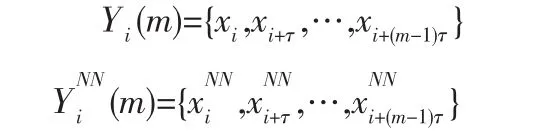
定义以下3个变量:
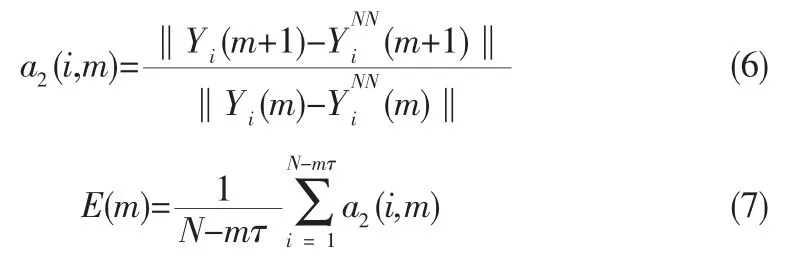
以及

如果时间序列是确定的,则嵌入维是存在的,即E1(m)将在m大于某一特定值m0后将不再变化。若时间序列是随机信号则E1(m)应逐渐增大,但在实际应用中对序列E1(m)是否缓慢变化已不容易,因此补充第二判断准则为:
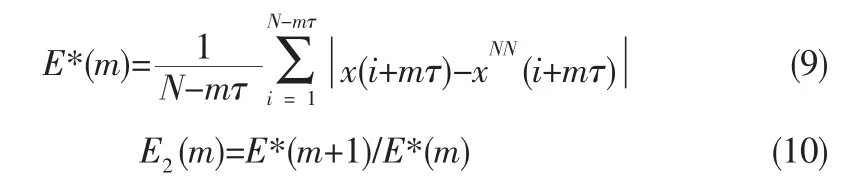
由于随机数据间没有相关性,E2(m)将恒等于1;而对于混沌时间序列,其相关性依赖于嵌入维数m,总存在一些m使得E2(m)≠1。因此通过E2(m)判定信号数据是随机还是确定序列。
3 海杂波动力学预测模型
根据前面介绍的知识,可以知道相空间重构的关键在于函数f的构造,然而f的精确解析式很难获得,只能通过某些技术来得到f的近似表达。实际上,本文正是利用小波神经网络作为近似的预测模型。
神经网络具有的强大的非线性处理能力和自学习能力,适合建立混沌背景噪声的预测模型。利用混沌时间序列对混沌背景重构相空间,使其与混沌背景噪声具有相同的基本动力学[5]特征,并通过设定合适的预测误差门限来检测掩埋在混沌背景中的有用微弱信号,并进一步对海杂波进行抑制[6]。基于神经网络的预测方法如图1所示。
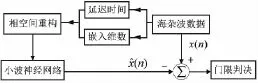
图1 基于神经网络的预测方法示意图Fig.1 The diagram of prediction method based on neural network
对于实测海杂波序列x(n),利用小波神经网络预测的具体方法如下:
1)对x(n)进行相空间重构,并求延迟时间τ和嵌入维数m。
2)确定神经网络结构以及数据的预处理。小波神经网络的输入层个数即为嵌入维数m,而输出层应只有一个节点,即输出海杂波的预测值。
3)训练神经网络。利用一组不含目标的纯海杂波数据x1(n)对网络进行训练。使之达到一定精度。
4)海杂波预测。利用训练好的网络预测另一组数据x2(n),得到预测值为(n),误差为ε(n)=(n)-x2(n),其均方差为R=,多次实验得到一个合适的门限值T,若均方差R大于T,则判定海面存在小目标;若均方差R小于T,则认为没有目标为纯海杂波。
4 基于遗传算法的小波神经网络
4.1 小波神经网络
本文采用的小波神经网络(WNN),通过把小波和神经网络紧密结合在一起,继承了神经网络的学习能力及小波变换的局部化特性,为混沌时间序列的预测提供了一条有效途径[7]。其中小波基函数为Morlet母小波基函数,公式为y=cos(1.75x)e-x2/2。同时本文中WNN权值参数修正采用梯度修正法,根据误差不断修正网络参数,使小波神经网络的预测输出接近实际输出。
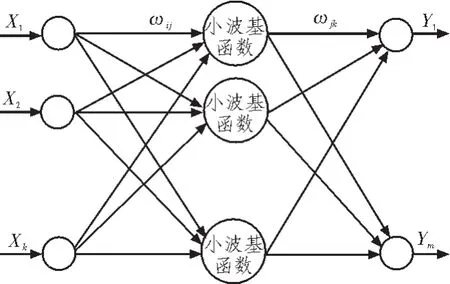
图2 小波神经网络拓扑结构Fig.2 The topological structure of WNN
小波神经网络算法训练步骤如下:
Step1:网络初始化。随机初始化网络连接权重ωij、ωjk、小波函数伸缩因子ak、平移因子bk,以及设置网络学习速率η。
Step2:样本分类。把样本分为训练样本和测试样本,其中训练样本用于训练网络,测试样本用于测试网络预测精度。
Step3:预测输出。把训练样本输入网络,计算网络预测输出并计算实际输出和期望输出的误差e。
Step4:权值修正。根据误差e修正网络权值和小波函数参数,是网络预测值逼近期望值。
Step5:判断算法是否结束,若没结束,返回Step3。
4.2 遗传算法优化小波神经网络
小波神经网络是根据误差能量函数,采用梯度下降法调整网络连接权值和伸缩平移尺度,容易陷入局部极小值和引起振荡效应。为此,本文使用全局搜索能力较强遗传算法来优化网络初始值。
遗传算法(GA)是模拟自然界遗传机制和生物进化论而成的一种并行随机搜索最优化方法。它把自然界“优胜劣汰,适者生存”的生物进化原理引入优化参数形成的编码串联群体中,按照所选择的适应度函数并通过遗传中的选择、交叉和变异对个体进行筛选,使适应度值好的个体被保留,适应度差的个体被淘汰,行的群体既继承了上一代信息,又优于上一代,反复循环直至满足条件。由于GA具有很强的全局搜索能力,而小波基函数具有良好的时频局部特性。两者的结合将得到一种既有全局优化搜索,又有良好局部优化求解性能的有效学习训练途径[8]。原理如图3所示。
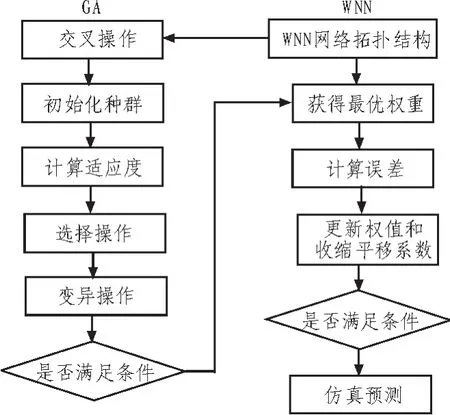
图3 遗传算法优化小波神经网络过程Fig.3 The procedure of GA optimizing WNN
GA优化WNN网络主要分为WNN网络结构确定、遗传算法优化权值和小波基函数收缩平移系数、WNN网络训练及预测[9]。其中WNN网络的拓扑结构是根据样本输入/输出参数个数确定,这样就可以确定GA优化参数的个数,从而确定种群个体的编码长度。
具体步骤如下:
Step1:初始化种群。随机产生L个结构,包括各个权值和小波参数4个部分组成,其结构长度为m×j+j+j+j×n
Step2:对神经网络的各个权值及伸缩平移参数进行编码,其形式如下:其中k=1,2,…,j并对编码后初始群体进行训练。
Step3:根据训练结果确定每个个体的适应度,定义Fitness=1/(1+E),其中E为预测输出和期望输出绝对误差。
Step4:若终止条件满足,则转Step7;
Step5:选择若干适应度最大的个体,直接继承给下一代。同时用父代适应度最大个体替代遗传操作后产生的最差个体;
Step6:对当前一代群体进行交叉和变异等遗传操作,产生下一代群体,转至Step3;
Step7:终止循环,得到最佳染色体。然后解码还原相应值。
5 实验及结果
本文的所采用的数据研究来源于加拿大McMaster大学实验室公开部分 IPIX雷达数据, 文件名为19931107_135603_starea,这里选用1 000个数据点作为样本,形成一个混沌时间序列{x(t),t=1,2,…1 000},分别用互信息法和伪邻近点法求得m=14,τ=12。构建网络模型,输入层节点数即为嵌入维数14,输出层节点个数为1,隐层节点个数为2m+ 1个即29个,网络结构为12-25-1。最后利用训练好的网络作为预测器,对后续200个海杂波数据点进行多步预测,得出预测值与实际值的曲线图像。利用WNN网络和GAWNN网络进行预测得到的曲线分别如图4,5所示。
图6反映GA在WNN网络结构寻优过程非常迅速,约迭代15次就找到了最优解,以后过程趋于稳定的全局最优解,而对比BP、WNN和GA-WNN各项指标如表1,可以看出基于GA-WNN在拟合精度逼近和预测精度方面都有较好的效果。
仿真结果表明,选用遗传小波神经网络算法可提高网络的预测性能、同时更能提高网络预测效率,对抑制海杂波的速度较快、抑制效果较好。实验证明,遗传小波神经网络不仅继承了小波分析的局部特性和神经网络的学习及推广能力,而且继承了遗传算法在寻优过程中具有全局性、快速性、适应性和鲁棒性的特点,是多层前向神经网络训练的一种理想算法。
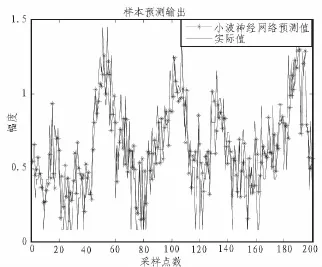
图4 小波神经网络预测曲线Fig.4 The prediction curve of WNN
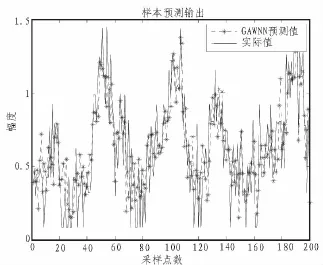
图5 GAWNN网络预测曲线Fig.5 The prediction curve of GAWNN
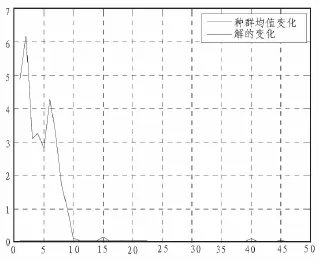
图6 GA迭代寻优的过程图Fig.6 The produce of iterative optimization

表1 WNN和GA-WNN网络预测效果比较Tab.1 The prediction resluts of WNN and GA-WNN
6 结束语
统计规律下的海杂波模型仅能从数据上进行拟合,不能很好的解释海杂波的演变过程和产生机理。本文利用给相空间重构理论,从混沌时间序列的角度来研究海杂波。分别用小波神经网络和遗传小波神经网络预测方法对海杂波进行预测,通过仿真实验可以看出,遗传小波神经网络很好继承了神经网络非线性处理能力和小波分析的时频局部特性,同时继承了遗传算法全局寻优的特点。遗传小波神经网络理论给海杂波混沌特性的预测与抑制提供了新的方法。
[1]Skolnik SMI.雷达手册 [M].北京:北京电子工业出版社,2003:504-531.
[2]王耀南.混沌神经网络模型及其应用研究综述[J].控制与决策,2006,21(2):122-127.WANG Yao-nan.Progress of chaotic neural networks and their applications[J].Control and Decision,2006,21(2):122-127.
[3]Takens F.Detecting strange attractor in turbulence[C]//Lecture Notes in Mathematics,1981,898:366-381.
[4]Cao L Y.Practical method for determining the minimum embedding dimension of a scalar time series[J].Physica D:Nonlinear Phenomena,1997,110(1-2):43-50.
[5]Haykin S,XiaoBoLi.Detection of signals in chaos[J].Proceedings of the IEEE,1995,183(1):94-122.
[6]韩长喜,李宗武.海杂波背景下基于混沌理论的目标检测[J].微型机与应用,2010(5):45-48.HAN Chang-xi,LI Zong-wu.Target detection in sea clutter based on chaos theory[J].Microcomputer and its Application,2010(5):45-48.
[7]陶小创.基于小波神经网络的混沌时间序列预测及应用[J].南京航空航天大学学报,2011,43(s):175-178.TAO Xiao-chuang.Chaotic time series prediction and its application based on wavelet neural network[J].Journal of Nanjing university of Aeronautics and Astronautics,2011,43(s):175-178.
[8]肖治平.遗传BP网络在机载雷达故障诊断中的应用研究[J].计算机测量与控制,2011,19(1):14-16.XIAO Zhi-ping.Research on application of GA-BP Neural Networks in Fault diagnosis of airborne radar[J].Computer Measurement and Control,2011,19(1):14-16.
[9]史峰.MATLAB神经网络30个案例分析[M].北京:航空航天大学出版社,2010:21-44,208-217.
Prediction of sea clutter based on GA-WNN
XU Ting
(School of Electronics and Information,Jiangsu University of Science and Technology Zhenjiang 212003,China)
A method for chaotic time series prediction based on genetic algorithm wavelet neural network(GA-WNN)is discussed by analyzing the theory of phase space reconstruction.According to the theory of Takens,calculate the phase space reconstruction for the time delay and embedding dimension.This paper presents the structure and algorithm of wavelet neural network and genetic algorithm,provide a reliable basis for the prediction of chaotic time series.In order to validate the reliability model,using IPIX radar datafor prediction,and results show the model of sea clutter can be based on known data predict future changes in value.Compared with the traditional neural network prediction,Genetic wavelet neural network prediction method better can get the fitting precision and prediction accuracy.
sea clutter;phase space reconstruction;WNN;GA
TN40
:A
:1674-6236(2015)18-0034-04
2014-12-04稿件编号:201412040
徐 婷(1989—),女,山东泰安人,硕士研究生。研究方向:智能信息处理。

