低信噪比微震P波震相初至自动拾取方法
贾瑞生,谭云亮,孙红梅,洪永发
(1.山东科技大学矿山灾害预防控制省部共建国家重点实验室培育基地,山东青岛 266590;2.山东科技大学信息科学与工程学院,山东青岛266590;3.山东科技大学矿业与安全工程学院,山东青岛 266590)
低信噪比微震P波震相初至自动拾取方法
贾瑞生1,2,谭云亮1,3,孙红梅2,洪永发2
(1.山东科技大学矿山灾害预防控制省部共建国家重点实验室培育基地,山东青岛 266590;2.山东科技大学信息科学与工程学院,山东青岛
266590;3.山东科技大学矿业与安全工程学院,山东青岛 266590)
摘 要:针对微震信号固有的低信噪比、非平稳性、随机性等特征,发展了一种基于希尔伯特-黄变换(HHT)和AIC准则相结合的震相初至自动拾取方法,该方法首先对含噪信号进行经验模态分解(EMD)及内蕴模态函数(IMF)重构,在保留微震信号固有特征基础上实现降噪;其次,基于Hilbert变换计算出归一化包络信号,通过设置包络阈值搜索震相初至的大致位置,并以该位置为基础为AIC函数选择合适的计算时窗以降低计算复杂度;最后,在选择的时窗内应用AIC准则计算出P波震相初至。应用该方法对随机选取的高、低信噪比两类共80个微震信号进行震相初至拾取,若以人工拾取结果为基准、时差在10 ms以内视为准确拾取,结果显示,高信噪比信号拾取准确率为100%,低信噪比信号拾取准确率为92%。
关键词:微震P波;震相初至拾取;经验模态分解;希尔伯特-黄变换;AIC准则
责任编辑:常 琛
贾瑞生,谭云亮,孙红梅,等.低信噪比微震P波震相初至自动拾取方法[J].煤炭学报,2015,40(8):1845-1852.doi:10.13225/ j.cnki.jccs.2014.1122
微震监测是预警冲击地压、煤与瓦斯突出、矿井突水等煤矿灾害事故的主要手段之一,目前已在微震信号频谱特征提取、灾害危险预警及防治等方面取得许多研究成果[1],这些成果的取得均建立在震源准确定位的基础之上,而震源准确定位技术的关键环节之一则是微震P波初至到时的准确拾取[2-3],因此微震P波震相初至自动拾取是微震监测系统的关键技术之一,是震源定位及震源机制解释的前提与基础。
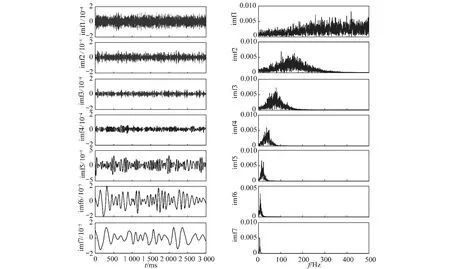
微震监测系统拾取的震动信号具有瞬态性、多样性及不确定性等特点,信号中夹杂有机械震动、环境噪声、电磁噪声等多种干扰信号,因此,如何在低信噪比信号中准确辨识微震P波到时十分困难。对于地震事件,目前已发展多种震相自动识别及拾取方法, 如Allen等基于时间域信号能量变化构建特征函数,提出了长短时均值比方法(STA/ LTA)[4-6];Akaike等基于地震波可划分为局部平稳段的假设,依据到达前后地震波形数据统计的差别,提出了判别震相初至的AIC准则[7-11];Saragiotis等基于地震波形的偏斜度和峰度提出了PAI-S/ K方法[12];常旭等应用分形理论对地震记录进行了有效的初至自动拾取[13];马强等综合应用STA/ LTA方法及AIC准则,基于Delaunay三角剖分剔除干扰信号,提出了多步骤的P波自动拾取方法[14];王继等应用单台Akaike信息准则和多台AIC最小二乘互相关方法,发展了震相自动精确检测技术,实现了流动地震台阵观测震相初至的自动拾取[15];刘劲松等通过分析STA/ LTA,AIC,PAI-S/ K等几种方法的原理及特点,提出了移动时窗峰度的快速算法和改进的峰度拾取初至算法[16]。以上方法均已在不同场合得到实际应用,能够实现对较高信噪比地震波的到时拾取,但当信号信噪比较低时可能会出现拾取结果精度不够甚至错误。对于微地震事件,其P波震相到时自动拾取的特殊性在于:相较于天然地震而言,微震信号频率较高、信噪比低,自动拾取震相初至易受外部噪声干扰。
为此,本文从信号分析理论入手,引入希尔伯特-黄变换对含噪微震信号进行降噪处理及包络分析,通过设置包络阈值为AIC算法选择合适的计算时窗,再在时窗内应用AIC方法,实现了低信噪比微震P波震相初至的自动拾取。
1 微震P波震相自动拾取算法分析
1.1 长短时均值比(STA/ LTA)法
设x(t)为t时刻P波垂向幅值,f(t)为高通滤波后的垂向幅值数据,则有
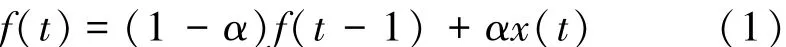
其中,α为高通滤波因子,由于P波震相在垂直方向幅值较大,可以通过构造信号特征函数来放大垂直方向幅值,常用的P波拾取特征函数为

STA/ LTA方法的基本原理是根据微震P波特征函数值的长短时均值比判断其初至[8-10],应用STA/ LTA的基本形式如下:
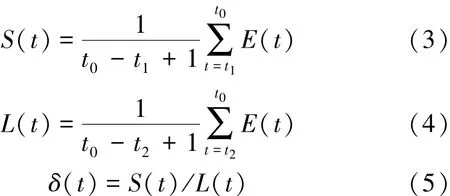
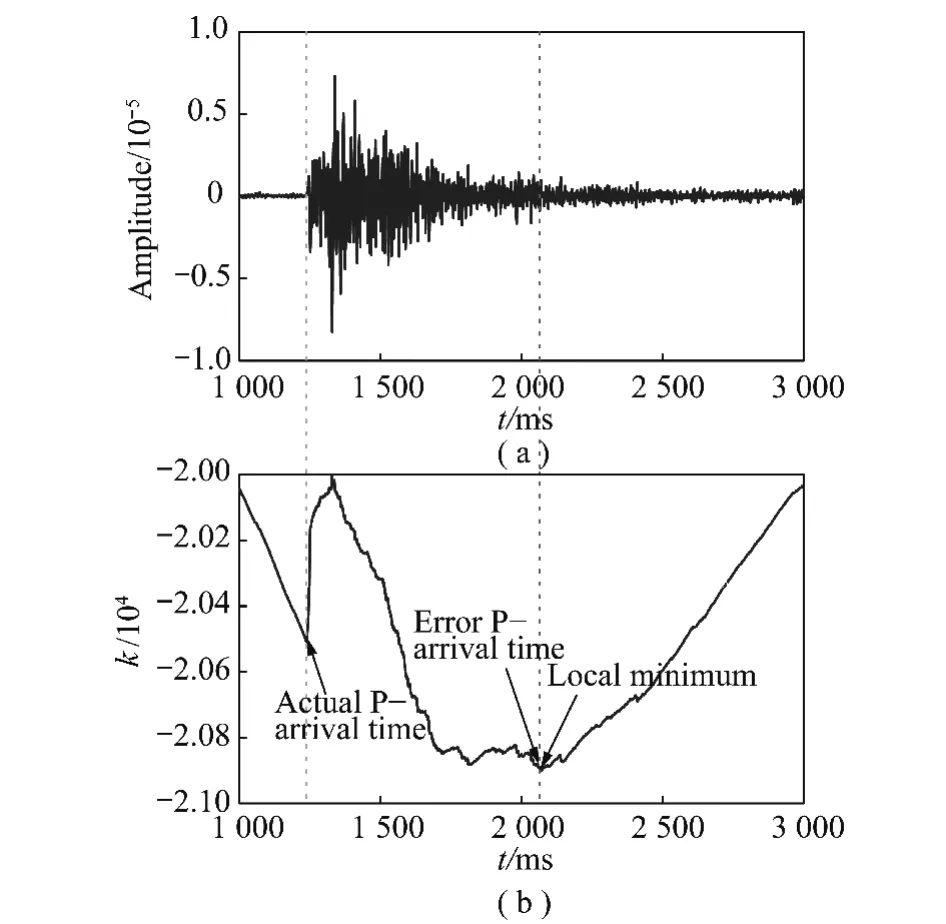
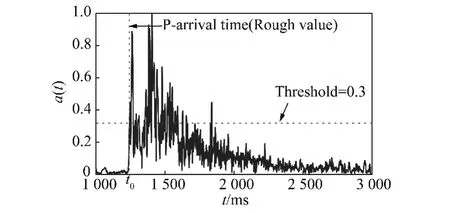
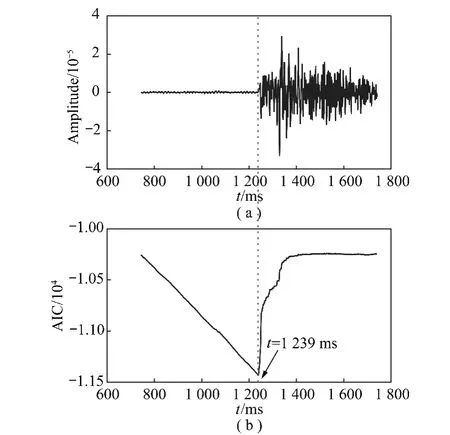
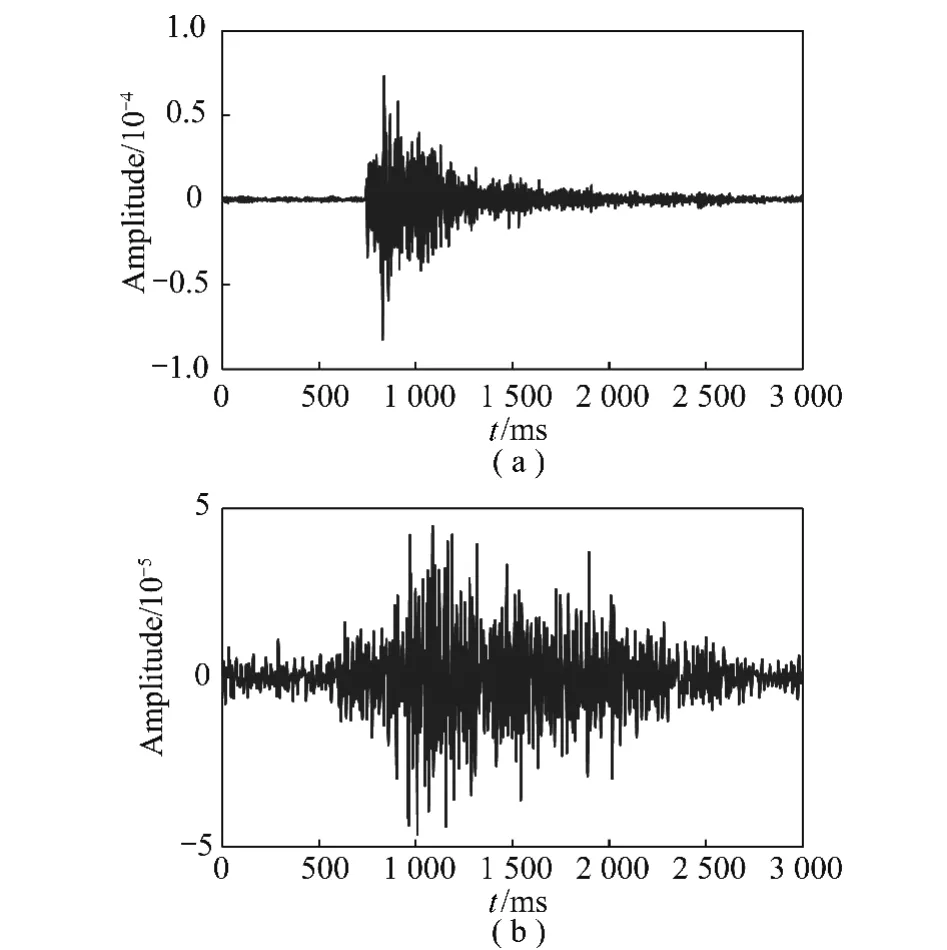
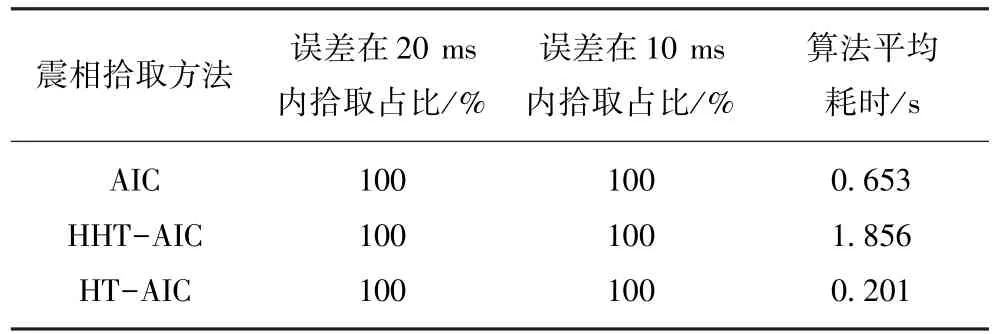
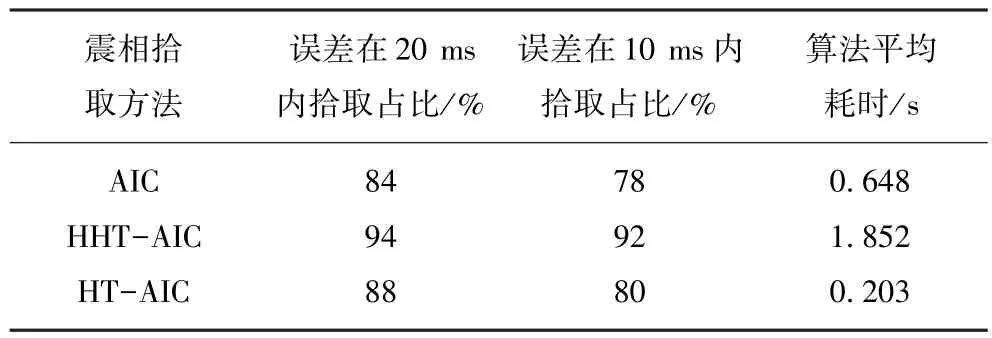
其中,t0为当前时刻;t1,t2为t0之前某时刻,且满足t2 图1 STA/ LTA法拾取P波到时Fig.1 Pick up P-arrival time based on STA/ LTA STA/ LTA方法的突出优点是算法稳定可靠、拾取效率高,但其触发点一般滞后于实际初至点(图1),当微震信号中存在干扰信号时,通常会产生震相初至点的错误判断[14],因而适用于高信噪比微震信号的震相初至拾取。 1.2 AIC方法 AIC方法的基本原理是求取地震信号AIC函数的局部最小值,Sleema提出了AR-AIC准则[10],它根据自回归过程将地震波形数据分成2个局部统计时段(图2),AR-AIC函数表示为 其中,k为两个局部统计时段分界点;p为AR过程阶数;l为地震波形数据长度;分别为2个局部统计时段的拟合误差;C为一个常数。为了求出震相初至,必须求出该函数中AR模型的阶数和系数,该方法计算复杂度较高,不利于震相初至的实时拾取。 图2 AR-AIC法拾取P波初至Fig.2 Pick up P-arrival time based on AR-AIC 不同于AR-AIC模型,Maeda提出直接由地震波形数据计算AIC函数[11],求取AIC函数的局部最小值(图3),该值对应的位置即为震相初至,AIC函数表示为 其中,x(i)(i=1,2,…,l)为地震波形离散数据;k的取值范围是数据窗口内所有采样点。 图3 微震波形和时窗[500,2 500]内的AIC函数曲线Fig.3 A microseismic signal and AIC function curve whentime window between 500 ms to 2 500 ms 对比以上2种AIC方法,后者不需要计算AR模型的阶数即可直接求取AIC值,在震相初至拾取实时性要求很高的情况下,是一种更加高效实用的算法,但是该算法需要在震相初至的附近寻找一个合适的时窗来计算AIC值,这是因为不同的时窗可能使AIC函数局部最小值出现的位置不同。图3(a),4(a)为同一个微震波形数据在不同时窗内的波形,图3(b),4(b)为对应的AIC函数曲线,其中图4由于时窗设置不合理导致震相初至拾取错误,如何合理选择时窗是AIC法准确拾取震相初至的关键问题之一。 图4 微震波形和时窗[1 000,3 000]内的AIC函数曲线Fig.4 A micro-seismic signal and AIC function figure whentime window between 1 000 ms to 3 000 ms 此外,微震监测过程中拾取的信号易受外界噪声干扰,使得AIC法震相初至拾取的精度大打折扣,有时还会造成微震事件的误拾取[10-11],因此,如何降低环境噪声对震相初至拾取的影响成为目前该领域研究的关键问题。由于微震信号及外部噪声具有随机性、非平稳性等特征,常规降噪方法(如Fourier方法)无法有效消除微震信号中夹杂的外部噪声,而HHT则能对非平稳信号进行EMD分解并重构,在保留信号固有非平稳特征基础上实现降噪。 2.1 EMD变换及信号降噪处理 Huang等提出了分析处理非平稳信号的EMD方法[17],即Huang变换,其核心是:任何非平稳信号都是由一些互不相同的、非正弦的、简单的IMF函数组成的,因此可将信号分解成从高频到低频若干个基本时间序列的组合,每个基本时间序列即是一个IMF分量。基于HHT的核心思想,含噪微震信号的EMD分解及消噪算法如下: (1)确定微震信号x(t)时间曲线上所有局部极大、极小值点,分别将其用3次样条函数拟合为原数据序列的上、下包络线,上、下包络线对应的坐标均值连接成均值线m1(t),由式(8)计算出h1(t),即 (2)判断h1(t)是否满足IMF函数所需条件,令 当SD值介于[0.2,0.3]之间时,筛选过程终止,得到信号x(t)的第1个IMF分量;若SD值不在[0.2,0.3]之间,此时把h1(t)看作新的时间序列曲线,重复以上步骤继续分解,则有 经过k次迭代后,当SD值介于[0.2,0.3]之间时,就得到了第1阶IMF分量h1k(t),将其记为c1(t),它表示微震信号的最高频部分。 (3)从原信号x(t)中减去该信号的高频部分c1(t),得到频率较低的信号残差r1(t): (4)将r1(t)看作一个新的信号序列,重复以上步骤,得到一系列的ci(t)和最后一个不可分解的信号残差r(t),则原信号可表达如下: (5)剔除高频IMF分量,对剩余的IMF分量进行重构,得到降噪后的微震信号: 图5 一个含噪微震信号的EMD分解Fig.5 Empirical mode decomposition of a micro seismic signal with noise 图5显示,含噪信号经EMD分解后得到7个IMF分量,这些IMF分量从高频到低频依次排列,由于微震频率范围一般介于0~200 Hz之间,观察IMF分量的频谱分布,可以判断出imf1为高频噪声成分,故可将其剔除,重构剩余的IMF即得到降噪后的微震有效信号。图6为EMD降噪前后微震信号的波形及频谱,对比图6(a),(c)可知,经过EMD降噪后较好地保留了信号的尖峰、突变及波形特征,说明EMD法能充分保留信号的瞬态非平稳特征;对比图6(b),(d)可知,图6(d)可清晰辨别出微震信号的时频特征,无用高频干扰噪声被有效滤除,为进一步识别震相初至奠定基础。 2.2 Hilbert变换及震相初至拾取算法 Hilbert变换是非平稳信号分析与处理的有效方法,实信号x(t)的Hilbert变换可定义[18]如下 Hilbert变换即是信号和时间倒数的卷积,实信号x(t)和它的Hilbert变换可组成解析信号: 其中, a(t)为解析信号的幅值;φ(t)为解析信号的相位,分别表示为 式中,a(t)为实信号x(t)的包络。 将降噪后的微震信号进行Hilbert变换并进行包络分析,即按时序将上下包络的绝对值相加并将其归一化处理,则图6(c)的Hilbert包络信号波形如图7所示,对同一类微震信号使用同一阈值(本文设为0.3)沿时间轴顺序搜索,当包络值大于设定阈值时,即可得到P波震相初至的大致位置t0,本例中t0= 1 243 ms。在经过HHT降噪后的微震信号波形上以t0为基准向前及向后分别取500个采样点作为计算时窗,在该时窗内应用AIC函数求解P波震相初至,求解结果如图8所示。 图6 去噪前后的微震信号波形及其频谱Fig.6 Microseismic signal waveform and its spectrum before and after de-noising 图7 Hilbert包络信号波形Fig.7 Waveform of Hilbert envelope signal 图8 时窗[744,1 743]内的微震波形和对应AIC函数曲线Fig.8 Microseismic signal when time window between 744 msand 1 743 ms and the corresponding AIC function curve 综上,基于HHT及AIC求解震相初至的改进算法(简称HHT-AIC法)如下:①对含噪微震信号进行EMD分解,按照频率从高到低获得一系列IMF分量,根据外部噪声特征对IMF分量进行剔除,并把剩余的IMF分量进行重构,实现微震信号的降噪;②对降噪后的微震信号进行Hilbert变换,求出其包络信号,并对其进行归一化处理;③设置包络阈值,沿时间轴查找第1个大于包络阈值的时刻,该时刻即为震相初至的粗略值,以该时刻为基准分别向前、向后各取500个采样点作为计算时窗;④在选取的时窗内应用式(7)计算AIC函数值,AIC函数局部最小值对应的时刻即为震相初至。 3.1 实验数据来源 为检验算法的有效性,我们分别选取一组高信噪比(标记为H组)及一组低信噪比(标记为L组)微震信号进行对比试验,其中H组信号来源于我国西部某水电站微震监测数据,该水电站所在地主要为硬岩结构,岩石破裂产生的微震信号起跳明显(图9(a)),监测环境较为理想,信号中噪声干扰较少,从中随机抽取30组微震信号用于实验;L组微震信号来源于我国西北某煤矿井下采场,属软岩地质构造,且机械振动、运输、放炮等产生的外部噪声较多,所采集的微震信号信噪比低,波形起跳不明显(图9(b)),从中随机抽取50组微震信号用于实验。 图9 高信噪比和低信噪比微震波形Fig.9 Micro seismic waveform with high signal to noise ratio and Micro seismic waveform with low signal to noise ratio 分别应用AIC方法及本文方法对上述2组不同类型的微震信号进行处理,并将其与人工拾取的震相初至结果对比,从拾取结果的正确率、算法耗时等方面进行评价。 3.2 实验结果及分析 应用Matlab编程实现AIC算法及HHT-AIC算法,对图9(a)所示的高信噪比微震波形进行震相初至拾取,与人工拾取的结果对比如图10所示。 图10所示的AIC及HHT-AIC两种拾取方法都获得了同样的震相初至时刻739 ms,在相同软硬件配置的PC机上,AIC法运算耗时0.641 s,HHT-AIC法耗时1.892 s,AIC法耗时最少,但AIC法在选择时窗大小及位置不合理时可能会出现图4(b)出现的错误拾取结果,故AIC法是不稳定的;HHT-AIC法包括EMD降噪(耗时1.689 s)、Hilbert包络分析及AIC函数计算(耗时0.203 s)等过程,计算复杂度较高,但当处理高信噪比信号时可以省去EMD降噪过程,仅保留Hilbert包络分析及AIC函数计算过程(以下称HT-AIC法),此时算法仅耗时0.203 s,大大低于AIC法的计算耗时,且能保持震相初至拾取精度不变,这是因为HHT-AIC法利用Hilbert变换进行包络分析时为AIC函数选择了合适的计算时窗(图10(c)),时窗内仅有1 000个采样点数据,大大降低了AIC函数的计算强度。 对H组中30个高信噪比微震信号进行处理,以人工拾取的震相初至作为参照,震相初至拾取结果见表1。其中AIC法的计算时窗为P波初至前750个至P波初至后2 250个采样点数据,时窗内共3 000个采样点数据;HHT-AIC时窗为P波初至前后各500个采样点数据,时窗内共1 000个采样点数据; HT-AIC法所采用的时窗位置及大小与HHT-AIC方法所采用的时窗相同。 从表1可以看出,对于H组中的高信噪比微震信号,3种方法均获得了准确率很高的震相初至拾取结果,对比它们的算法平均耗时,可以看出HT-AIC算法耗时最少。 图10 使用AIC法及HHT-AIC法拾取高信噪比微震P波初至结果对比Fig.10 Detection on micro seismic P-arrival time by using AIC and HHT-AIC method under high SNR 表1 高信噪比微震信号震相初至拾取结果Table 1 Result of detection on microseismic P-arrival time 分别应用AIC,HHT-AIC方法对图9(b)所示的低信噪比微震信号进行震相初至拾取,与人工拾取的结果对比如图11所示。图11(a)为原始微震信号,起跳位置较为模糊,即使人工辨识信号起跳点也存在一定困难,通过信号局部放大,人工拾取的震相初至t=631 ms;图11(b)为未经消噪处理直接应用AIC法求取的震相初至t=2 326 ms,拾取结果出现错误; 图11(c)为经过EMD降噪后的微震信号,相较于图11(a)而言信号波形较为清晰,且充分保留了微震信号的随机非平稳特征;图11(d)为在消噪基础上应用HHT-AIC法计算得到的震相初至t=617 ms,计算结果与人工拾取结果相比误差在20 ms之内,说明HHT-AIC法能有效处理低信噪比信号震相初至的自动拾取,算法具有较强的抗噪性能。 从算法耗时来看,AIC方法耗时0.635 s,但自动拾取的震相初至出现错误; HHT - AIC法耗时1.912 s,虽然算法耗时较长,但获得了正确的拾取结果。若在图11(a)所示的微震波形上直接应用HTAIC法,算法耗时0.204 s,但拾取的震相初至为927 ms,与人工拾取结果631 ms相比产生了较大误差,这是因为该含噪信号波形起跳不明显,HT-AIC算法通过包络阈值搜寻震相初至的大致位置出现了偏差,导致为AIC函数的选取计算时窗不合理,从而使AIC函数计算得到的震相初至出现较大误差。因此,HT-AIC算法在处理低信噪比微震信号震相初至拾取时也是不稳定。 对L组中50个低信噪比微震信号进行处理,以人工拾取的震相初至作为参照,震相初至拾取结果见表2。表2中HHT-AIC法震相初至的拾取准确率最高,而HT-AIC法耗时最少。综合表1和2的拾取结果可以看出:对于高信噪比微震信号,HT-AIC法利用Hilbert变换对信号震相初至位置进行了粗略判定,为AIC函数选择了位置及大小合适的计算时窗,有效降低了AIC函数的计算强度,因而能在保持较高识别准确率的前提下使算法耗时最少;但HT-AIC方法在处理低信噪比微震信号时,如果不对含噪信号进行降噪处理,仍会导致计算时窗位置选择不合理,最终出现震相拾取结果错误;HHT-AIC法则首先应用EMD法对低信噪比微震信号进行降噪,提高了信号的信噪比,然后再应用HT-AIC算法实现震相初至的自动拾取,识别准确率比AIC法提高约10%,比HT-AIC法提高约6%。 图11 使用AIC法及HHT-AIC法拾取低信噪比微震P波初至结果对比Fig.11 Detection on micro seismic P-arrival time by using AIC and HHT-AIC method under low SNR 表2 低信噪比微震信号震相初至拾取结果Table 2 Result of detection on microseismic P-arrival time 3.3 关于震相自动拾取方法的讨论 AIC算法在时窗恰好包含有震相初至前后各一段波形的前提下,能够得到较好的拾取结果,故AIC算法适用于已知震相初至大致位置的情况,工程上通常与STA/ LTA法组合使用,即首先使用STA/ LTA法获取震相初至的大致位置,再以该位置为基础向前及向后各取一段数据作为AIC函数的时窗计算出震相初至位置,但在处理低信噪比微震信号时,应用AIC 及STA/ LTA方法时震相初至辨识的准确率均显著下降,算法抗噪性能较差。 HHT-AIC算法通过信号的EMD分解与IMF分量重构实现降噪,充分保留了微震信号固有的随机非平稳特征,并在消噪滤波的上应用Hilbert变换求得归一化包络信号波形,通过设定包络阈值搜索震相初至的大致位置后,再应用AIC法求解震相初至,因而HHT-AIC算法具有较强的抗噪性能,在相同信噪比情况下,震相初至辨识的准确率显著提高。 (1)对于高信噪比微震信号,HT-AIC方法能依据Hilbert变换及包络阈值为AIC函数确定计算时窗位置及大小,包络阈值参数选取简单,自动拾取的震相初至与人工拾取结果一致,误差在10 ms内拾取占比为100%,且算法实时性强,克服了传统AIC方法由于时窗选择不合理造成初至错误拾取的不足。 (2)对于低信噪比微震信号,HHT-AIC方法基于EMD分解及IMF重构两个过程对含噪信号进行降噪,充分保留了微震信号固有的瞬态非平稳特征,在此基础上再应用HT-AIC方法实现震相初至的自动拾取,通过实验与人工拾取结果相比,时差在10 ms内的微震信号占比为92%,自动拾取准确率高于AIC方法及HT-AIC方法,表现出较强的抗噪性能;不足之处是算法复杂度较高,但以牺牲时间为代价换取精度也是惯常的选择。 参考文献: [1]齐庆新,窦林名.冲击地压理论与技术[M].徐州:中国矿业大学出版社,2008:32-38. [2]巩思园,窦林名,马小平,等.煤矿矿震定位中异向波速模型的构建与求解[J].地球物理学报,2012,55(5):1757-1763. Gong Siyuan,Dou Linming,Ma Xiaoping,et al.Study on the construction and solution technique of anisotropic velocity model in the location of coal mine tremor[J].Chinese Journal of Geophysics, 2012,55(5):1757-1763. [3]朱权洁,姜福兴,王存文,等.微震波自动拾取与多通道联合定位优化[J].煤炭学报,2013,38(8):397-403. Zhu Quanjie, Jiang Fuxing, Wang Cunwen, et al.Automated micro-seismic event arrival picking and multi-channel recognition and location[J].Journal of China Coal Society,2013,38(8):397-403.[4]Allen R V.Automatic earthquake recognition and timing from single traces[J].Bull.Seismol.Soc.Amer.,1978,68 (5):1521 -1532. [5]Allen R V.Automatic phase pickers:Their present use and future prospects[J].Bull.Seismol.Soc.Amer.,1982,72(6):225-242.[6]Baer M,Kardolfer U.An automatic phase picker for local and tele-seismic events[J].Bull.Seismol.Soc.Amer.,1987,77 (4): 1437-1445. [7]Akaike H.Information theory and an extension of the maximum likelihood principle[A].2ndInternational Symposium on Information Theory (Tsahkadsor)[C].1971:267-281. [8]Takanami T,Kitagawa G.Multivariate time-series model to estimate the arrival times of S-waves[J].Computers and Geosciences, 1993,19(2):295-301. [9]Leonard M,Kennett M B L N.Multi-component autoregressive techniques for the analysis of seismograms[J].Phys.Earth Planet.Interiors,1999,113(1-4):247-264. [10]Sleeman R,Orild V E.Robust automatic P-phase picking:an online implementation in the analysis of broadband seismogram recordings [J].Phys.Earth Planet.Interiors,1999,113(1-4):265-275. [11]Maeda N.A method for reading and checking phase times in autoprocessing system of seismic wave data[J].J.Seismol.Soc.Jpn., 1985,38(3):365-379. [12]Saragiotis, Christos D.PAI-S/ K: A robust automatic seismic P phase arrival identification scheme[J].IEEE Transactions on Geosciences and Remote Sensing,2002,40(6):1395. [13]常 旭,刘伊克.地震记录的广义分维及其应用[J].地球物理学报,2002,11(6):839-846. Chang Xu,Liu Yike.The generalized fractal dimension of seismic records and its application[J].Chinese Journal of Geophysics, 2002,11(6):839-846. [14]马 强,金 星,李山有,等.用于地震预警的P波震相到时自动拾取[J].地球物理学报,2013,56(7):2313-2321. Ma Qiang,Jin Xing,Li Shanyou,et al.Automatic P-arrival detection for earthquake early warning[J].Chinese Journal of Geophysics,2013,56(7):2313-2321. [15]王 继,陈九辉,刘启元,等.流动地震台阵观测初至震相的自动检测[J].地震学报,2006,28(1):42-51. Wang Ji,Chen Jiuhui,Liu Qiyuan,et al.Automatic onset phase picking for portable seismic array observation[J].Acta Seismologica Sinica,2006,28(1):42-51. [16]刘劲松,王 赟,姚振兴.微地震信号到时自动拾取方法[J].地球物理学报,2013,56(5):1660-1666. Liu Jinsong,Wang Yun,Yao Zhenxing.On micro-seismic first arrival identification:A case study[J].Chinese Journal of Geophysics, 2013,56(5):1660-1666. [17]Huang N E,Zheng S,Steven R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear non-stationary time series analysis[A].Proceedings:Mathematical,Physical and Engineering Sciences [C].London: The Royal Society Press,1998: 903-995. [18]Rashid A.IIR discrete-time Hilbert transformers[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1987,35(8): 1116-1119. Jia Ruisheng,Tan Yunliang,Sun Hongmei,et al.Method of automatic detection on micro-seismic P-arrival time under low signal to noise ratio[J].Journal of China Coal Society,2015,40(8):1845-1852.doi:10.13225/ j.cnki.jccs.2014.1122 Method of automatic detection on micro-seismic P-arrival time under low signal-to-noise ratio JIA Rui-sheng1,2,TAN Yun-liang1,3,SUN Hong-mei2,HONG Yong-fa2 (1.State Key Laboratory of Mining Disaster Prevention and Control Co-founded by Shandong Province and Ministry of Science and Technology,Shandong University of Science and Technology,Qingdao 266590,China;2.College of Information Science and Engineering,Shandong University of Science and Technology,Qingdao 266590,China;3.College of Mining and Safety Engineering,Shandong University of Science and Technology,Qingdao 266590,China) Abstract:According to the low signal-to-noise ratio,non-stationary,and inherent randomness of micro-seismic signals, a new method based on Hilbert-Huang Transform (HHT) and AIC criterion was proposed.Firstly,to implement denoising and filtering,the signals with noise were decomposed with empirical mode decomposition (EMD) and then reconstructed with intrinsic mode function (IMF);Secondly,based on the Hilbert transform,the normalized envelope signal was calculated,the coarse position of P-arrival was searched by setting the envelope threshold,and on the basis of the position,the time window of AIC function was determined;Finally,the P-arrival time was calculated by using AIC criterion in the selected time window.This method was applied to 80 random micro-seismic signals with both high SNR and low SNR.Considering the manual picking results as a benchmark and the time difference within 10 ms as an accurate result,the result shows that for the signals with high SNR,the picking accuracy is 100%.For the signals with low SNR,the accuracy is 92%. Key words:micro-seismic P-arrival;seismic phase first arrival identification;empirical mode decomposition;Hilbert-Huang transform;Akaike information criterion 作者简介:贾瑞生(1972—),男,安徽砀山人,教授,博士。E-mail:jrs716@163.com 基金项目:山东省自然科学基金资助项目(ZR2013EEM019);国家“十二五”科技支撑计划资助项目(2012BAK04B06) 收稿日期:2014-08-30 中图分类号:TD32 文献标志码:A 文章编号:0253-9993(2015)08-1845-08
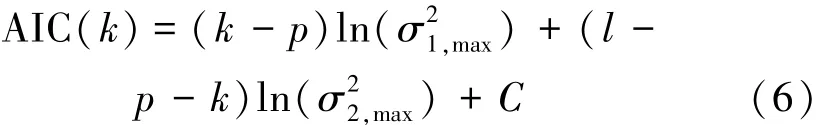

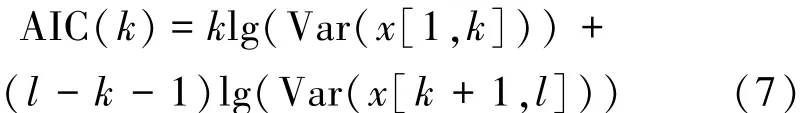

2 对震相自动拾取算法的改进

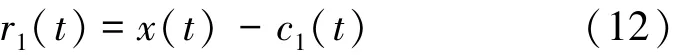

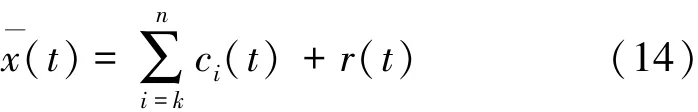

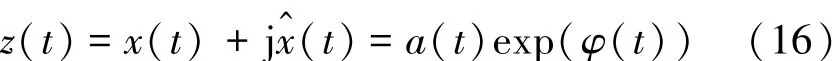
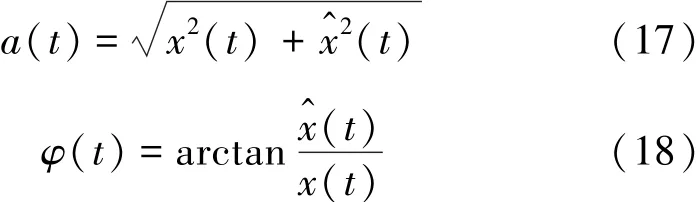

3 算法检验及讨论


4 结 论

