基于短时Fourier变换的瑞雷面波相速度提取

陈亚东，戴华林

(天津城建大学 a. 计算机与信息工程学院；b. 计算中心，天津 300384)

信息科学与技术

基于短时Fourier变换的瑞雷面波相速度提取

陈亚东a，戴华林b

(天津城建大学 a. 计算机与信息工程学院；b. 计算中心，天津 300384)

瑞雷面波勘探的主要思想是利用瑞雷面波的频散特性来反映浅层地质问题.在分析常规Fourier变换提取瑞雷面波相速度的局限性的基础上，提出采用短时Fourier变换方法对实际资料进行处理，结果表明：短时Fourier变换提取瑞雷面波相速度的方法具有较高的准确性和可靠性，有很好的应用效果和发展前景.

瑞雷面波；频散特性；时-频分析；短时Fourier变换

瑞雷面波勘探主要是根据瑞雷面波的频散特性，通过对原始数据的分析，并进一步反演，以获得浅层、超浅层的地质结构及介质物理参数．近些年来，该方法发展迅速，方兴未艾，广泛应用于交通、水电、桥梁和地基勘察等方面，已逐步发展成为一套独立的、完整的勘探方法[1]．瑞雷面波勘探的基本工具是常规Fourier变换，但这种方法只能反映信号的整体特性，不能反映信号的局部特征，尤其是不能同时观测信号在时间域和频率域的变化情况．这在信号分析中就面临一对最基本的矛盾：时域和频域的局部化矛盾．笔者提出采用短时Fourier变换方法，以实现对瑞雷面波相速度的有效提取．

1 瑞雷面波勘探的理论基础

瑞雷面波勘探最根本的依据就是瑞雷面波在层状介质中传播时具有频散特性．弹性波理论证明，在自由空间和弹性半无限介质中，瑞雷面波传播时的法向应力和切向应力都为零，此时，瑞雷面波无频散特性，但这只是理想状态．在实际中，地表总有一层薄的疏松覆盖层，这就导致了法向应力不再为零，而切向应力仍为零．正是由于法向应力的改变，使得瑞雷面波在层状介质中传播时的速度发生了变化[2]，表达式为

从式(1)可以看出，瑞雷面波的相速度VR是频率ω的函数，因此疏松层的存在导致了瑞雷面波的频散．瑞雷面波的频散特性为人们提供了提取瑞雷面波相速度的可能性，进而，不同相速度的单色波，看到的是不同深度的介质性质，组合起来，即可以清晰地得到近地表附近的介质分布情况．因此，工程中利用瑞雷面波进行浅层、超浅层勘探有着积极的意义．

2 瑞雷面波相速度的提取方法

2.1 常规Fourier变换方法

将接收到的信号进行一系列的谱分析，得到两信号的自功率谱、互功率谱及相干函数；由互功率谱得到两信号在波传播过程中由于时间滞后所产生的相位差，即求得实测的频散曲线，再由成层地基动力学理论及反分析法，求得剪切波速度和深度的关系．其计算过程简述如下[3]．

(1)时间域向频率域的转换，即得到N道信号X1(t),X2(t),X3(t),…,Xn(t)的频谱[4]

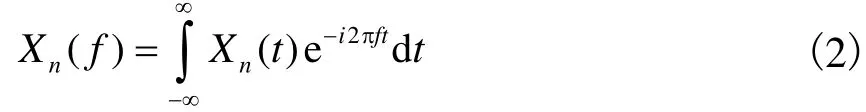
(2)自功率谱、互功率谱和相位差的求取．利用相邻道的频谱可求出Xn-1(t)、Xn(t)的自功率谱

因此，Xn(t)、X(n-1)(t)的互功率谱Sn(n-1)(f)可计算求得

由互功率谱式(4)可求出相位差Δφ．

(3)相速度的确定．利用公式

可计算出离散点f的瑞雷面波平均速度，其中，VR为瑞雷面波平均速度；f为频率；Δx为相邻道之间的距离，一般情况下，Δx应小于一个波长．

(4)深度-速度函数的确定．在国内外的瑞雷面波勘探中，确定深度和速度一般采用所谓的半波长解释法[5]，即勘探深度是波长的一半，即

(5)绘制频散曲线．根据以上分析计算，即可得到深度-速度函数(H-VR)，进一步可以得到测试点的频散曲线，如图1所示．实际资料见图1a．该记录为12道，1,024个采样点，道间距为2,m，采样周期为0.000,5,s，偏移距为零；首先对原始记录进行滤波，去除反射波的干扰，图1b为滤波后结果；再将信号从时间域转换到频率域，得到信号的f-k图，在有效频率范围内拾取每一f极大值及相应的k值，即频散曲线的屏幕拾取，见图1c；据此计算相速度，最后绘制频散曲线图1d．

图1 常规Fourier变换处理实际资料

由此可见该方法存在以下缺陷：①利用互相关谱求相位差，受到Fourier 变换本身的局限，由于Fourier变换的相位变化范围为［-π,π］之间，这要求两个检波点距离不得大于接收到的波的最小波长，否则计算所得相位差可能与实际相差2π的整数倍，这就造成Fourier 变换提取的相位差可能是不真实的；②对于频率很低的单色波，在满足上述检波器距离的要求下，其相位差可能很小，甚至趋于零，而相位差Δφ在式(5)中作为分母，这样，一个极小的误差Δφ都会带来极大的速度误差．

2.2 短时Fourier变换方法

针对常规Fourier变换本身的局限性，人们相继提出了短时Fourier变换、小波分析以及Gabor展开等[6]．与常规Fourier变换不同，短时Fourier变换可

以同时获得时间(空间)域和频率域的分辨率，它既可以确定信号的频率成分，又可以确定某一频率在时间域的分布规律．其基本思想是将非平稳信号看成分段平稳信号，那么通过在原始信号上加固定窗，然后由窗口在原始信号上用平移的方法，就可以得到原始信号的时频谱[7]．

对于一个给定时间宽度的窗函数r(t)，沿时间轴滑动，则信号s(t＇)的短时Fourier变换定义为[8]

式中：“*”表示复共轭；r(t)是有限支集的函数．在这个变换中，e-j2πft＇起着频限的作用，r(t)起着时限的作用．随着时间t的变化，r(t)所确定的“时间窗”在t轴上移动，使s(t')“逐渐”进行分析．由式(7)可以看出，正是窗函数r(t)的时(间)移(位)和频(率)移(位)使短时Fourier变换具有了局域特性，它既是时间的函数，又是频率的函数．式(7)即为信号s(t＇)的时频分布函数，利用这个时频分布函数，可以轻松地求得瑞雷面波的相速度．

(1)对相距为Δx的N个检波器接收到的信号作时-频分析，可以得到N个时频分布图．

(2)对于每一个固定频率f，分别在每个时频分布图上寻找该频率能量极值点所对应的时间t1,t2,…，tN，进而可以计算出该频率在相邻两个时频分布图上的时间差Δt=tn-tn-1(0＜n≤N)，这个时差就是该频率以其相速度在相邻两个检波器之间传播形成的时间差．

(3)相速度的计算．利用公式[9]

可计算出每一固定频率f在相邻两道传播的相速度．对于实测的信号，可能有N道记录，可以对其作统计分析，得到相速度的统计量．

(4)频散曲线的绘制．根据第(3)步的计算结果，可以绘出瑞雷面波相速度随频率的变化曲线，如图2所示．对上述实际记录选取其中第7道和第9道短时Fourier变换，得到的时频分布见图2a、图2b．在两道信号的时频图上寻找相同频率的极值点位置，如图2a和图2b中14,Hz的极点(即图中白色十字游标中心位置)分别位于96，102,ms位置上，则该频率的单色波传播在两个道间形成的时差为6,ms，相速度为2/0.006＝333.4,m/s．对每一道数据作短时Fourier变换，得出相速度随频率变化的统计量，进而绘制频散曲线图2c．

显然，短时Fourier变换处理结果比常规Fourier变换的精度要高，漏掉的岩层被显示出来．由于短时Fourier变换纵横坐标控制精确，其稳定性强，该方法在瑞雷面波相速度提取中必将有广阔的应用前景．

图2 短时Fourier变换处理实际资料

3 结 论

短时Fourier变换克服了常规Fourier变换利用互相关谱法求相位差，进而再求相速度的缺陷．短时Fourier变换求取相速度的精度取决于时间分辨率，而对于合格的面波勘探资料，完全可以保证短时Fourier变换的时间分辨率，从而得到的是确切的相速度．因此，该方法可以极大地提高瑞雷面波相速度

提取的稳定性和可靠性，从而提高工程勘探地基土分层的准确性．

［1］ 杨成林. 瑞雷波勘探[M]. 北京：地质出版社，1993.

［2］ 张大洲，熊章强，秦 臻. 基于 Fourier 变换的瑞雷面波分离提取及实例分析[J]. 中南大学学报：自然科学版，2010，41(2)：643-648.

［3］ 程乾生. 信号数字处理的数学原理[M]. 北京：石油工业出版社，1979.

［4］ CHEN Xiao. Leaky Rayleigh wave at the interface between inviscid fluid and solid[J]. Chinese Journal of Theoretical and Applied，2010，42(1)：51-55.

［5］ 胡昌华，周 涛. 基于MATLAB的系统分析与设计——时频分析[M]. 西安：西安电子科技大学出版社，2002.

［6］ LIU Bin，DONG Shiyun，XU Binshi，et al. Study on surface stress measurement of laser cladding Fe-based alloy coating based on Rayleigh wave signal analysis [J]. Advanced Materials Research，2012，399/400/401：2,177-2,180.

［7］ PHAM-CHI Vinh，PETER G M. Improved approximations of the Rayleigh wave velocity[J]. Journal of Thermoplastic Composite Materials，2008，21(4)：337-352.

［8］ LI Aibing. Influence of surface stress and atomic defect generation on Rayleigh wave propagation in laser-excited solids[J]. Physica B：Condensed Matter，2013，42(1)：28-33.

［9］ 丰 赟，周竹生，沙 椿. 瑞雷波数值模拟中的数值频散校正策略及实例分析[J]. 中南大学学报：自然科学版，2012，43(6)：2,231-2,237.

The Rayleigh Surface Wave Phase Velocity Extraction Based on Short-time Fourier Transform

CHEN Ya-donga，DAI Hua-linb
(a. School of Computer and Information Engineering；b. Computing Center，Tianjin Chengjian University，Tianjin 300384，China)

The main idea of Rayleigh wave exploration is making use of frequency dispersion of Rayleigh wave to reveal geology structure of low layer. Based on the limitation analysis of extraction of the Rayleigh wave speed by conventional Fourier transform,authors present a new use actual data processing method based on the short-time Fourier transform. The results show that the extraction of the Rayleigh wave speed by short-time Fourier transform is high accuracy and reliability,which has a good application effect and development prospects.

Rayleigh wave；frequency dispersion；time-frequency analysis；short-time Fourier transform

P631.4

A

2095-719X(2015)04-0299-04

2014-12-02；

2015-04-20

天津市自然科学基金(10JCYBJC00600)

陈亚东（1974—），女，内蒙赤峰人，天津城建大学副教授，硕士．