城市轨道交通车辆悬挂系统故障诊断方法研究

（广西制造系统与先进制造技术重点实验室（广西大学机械工程学院），广西 南宁 530004）

伴随着我国城市建设的蓬勃发展，城市交通问题给社会带来了巨大的压力，例如交通的拥堵和瘫痪，资源和能源的浪费，空气环境的污染和恶化等。在当今世界各大型城市，轨道交通在公共交通系统中占据重要的地位。而轨道交通车辆的运行安全性和乘坐舒适性是制约城市轨道交通发展的瓶颈。城市轨道交通车辆悬挂系统是轨道车辆走行部的关键组成部件，悬挂系统的性能直接影制约着车辆运行的安全性和车辆乘坐的舒适性。针对于悬挂系统的在线实时故障状态监测对车辆的安全、稳定运行起着举足轻重的作用，因而，探求实时、高效、可靠的悬挂系统故障诊断方法是国内外诸多研究学者攻克的难题。

目前，国内外对车辆悬挂系统故障诊断方法众多，有基于IMM算法的车辆悬挂系统故障诊断[1-2]，基于观察法的车辆悬挂系统故障诊断[3-4]，基于多元统计分析的故障诊断方法[5-7]等，然而这些方法只能在线监测出故障报警，不能进行故障分离。而魏秀坤教授提出了基于多传感信息融合技术[8]和基于相似度比测量的车辆悬挂故障诊断方法[9]。本文主要通过对车辆悬挂系统国内外研究现状及其所用不同算法进行研究，分析不同研究算法在车辆悬挂系统故障诊断中的优缺点，为探索车辆悬挂系统故障诊断方法提供依据。

1 轨道交通车辆悬挂系统的动态模型

城市轨道车辆主要由车体、转向架、轮对和悬挂系统组成，悬挂系统分为一系悬挂系统和二系悬挂系统。一系悬挂位于轮对与转向架构架之间，二系悬挂位于车体与转向架构架之间，悬挂系统支撑着车体和转向架，起到缓解由轨道不平顺引起的激扰，平衡轴重分配，保证车辆的稳定性和舒适性等作用。对车辆悬挂系统研究，主要分析轨道交通车辆实际工况运行特性，建立动态数学模型，采用先进传感技术捕获检测设备的故障信息，有故障诊断技术识别故障类型。由此可见，车辆数学模型的建立是车辆悬挂系统故障诊断的前提。

在运行过程中车体和转向架运动包括垂向位移、横向位移、点头和侧滚，每一种运动特性对应一个自由度，通过对轨道交通车辆的车体和转向架使用牛顿运动定律分析以及利用车载加速度传感器对车体和转向架振动信号的采集，获得整车的运动模型。

1.1 车辆垂向悬挂系统建模

车辆在实际运行过程中受到轨道高低不平顺引起激扰，造成车辆的垂向振动、点头和侧滚运动，可以利用车载加速度传感器和倾角传感器对车体和转向架实时监测，构建轨道车辆垂向悬挂系统动态数学模型。轨道车辆在直行工况下动态模型如图1所示。车辆运动过程中伴随着车体和转向架的点头和侧滚运动，会造成移动的位移量，位移量关系如图2所示。

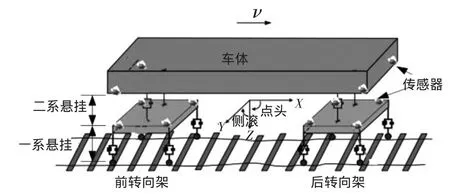
图1垂向悬挂系统模型

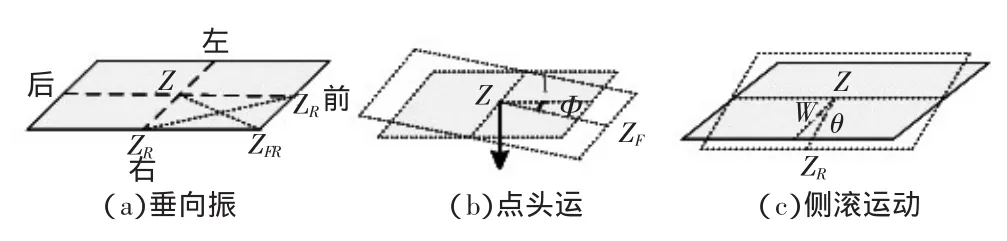
图2角度位移与中心位移关系

图2（a）反映了垂向振动中中心振动位移与各边质点的位移关系；2（b）反映了点头运动中角位移量与中心振动位移的关系；2（c）反映了侧滚运动中角位移量与中心振动位移的关系。车体与转向架的振动位移量由车载加速度进行双重积分获得，而对于车体和转向架的侧滚位移量和点头位移量通过如下计算[10]。

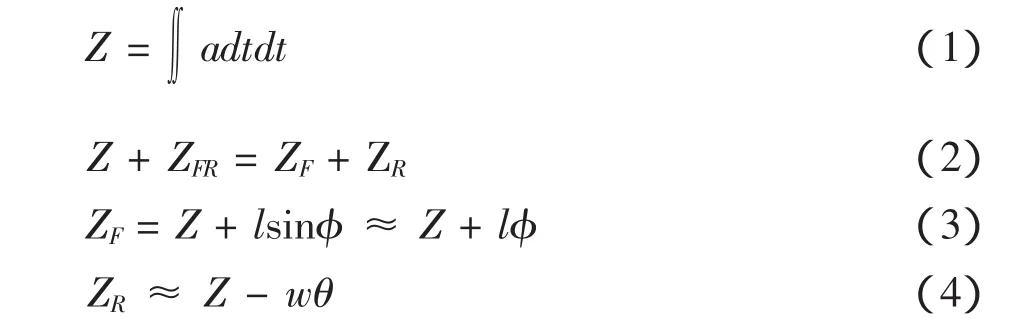
1.2 车辆横向悬挂系统建模

轨道车辆悬挂系统横向振动由轨道的水平不平顺引起，车辆横向悬挂系统数学建模主要参考车体、前转向架、两个轮对和一系二系悬挂装置在内的7自由度，车辆在直线运行工况时系统动态模型如图3所示。

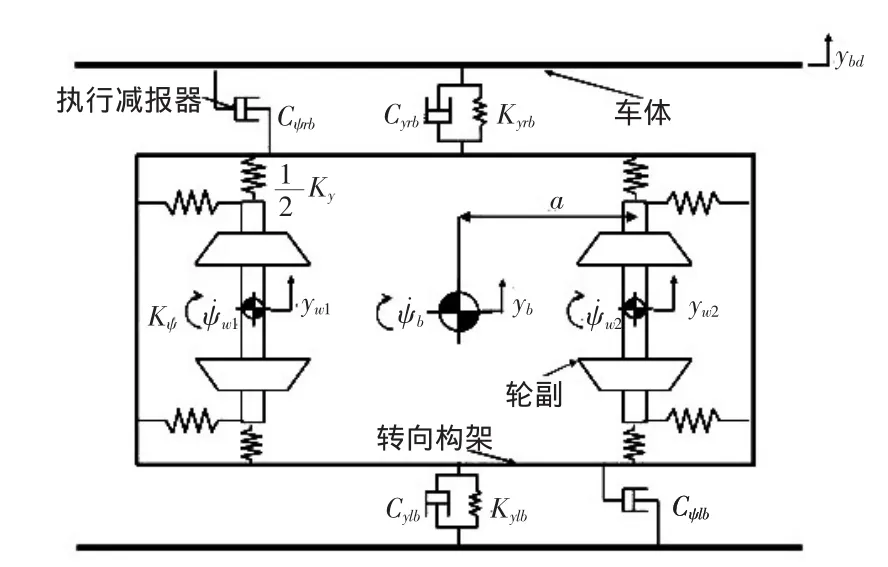
图3横向悬挂系统模型

1.3 车辆悬挂系统的状态空间方程

城市轨道交通车辆在运行过程中，悬挂系统的振动具有耦合性和非线性。在悬挂系统数学建模时常采用线性模型去拟合非线性特性，或将非线性特性分段，然后采用线性模型进行分段拟合，或建立复杂的非线性模型。车辆悬挂系统的状态空间方程如下：

线性状态空间方程[11-12]：

非线性状态空间方程[13]：

2 轨道交通车辆悬架系统故障诊断方法

城市轨道交通车辆在运行过程中，由于受到来自轨道的激扰，车辆悬挂系统常出现一系悬挂和二系悬挂弹簧和阻尼衰减失效等问题，严重影响了车辆运行的安全性和乘坐的舒适性。解决此类问题传统方法是各运营段定期检修，而效果并不理想，采用车辆悬挂系统在线故障诊断技术早期发现故障问题可有效地保证车辆运行的安全性和舒适性。

2.1 基于多元统计分析的车辆悬挂系统故障诊断方法

多元统计分析故障诊断方法是数据驱动的故障诊断方法中重要的一种，利用多元投影方法将多变量的样本空间分解成较低维的投影子空间和相应的残差子空间，设置统计量并对统计量进行分析，以达到检测和诊断故障的目的。多元统计分析方法主要包括主元分析法（PCA）、偏最小二乘法（PLS）、对立主元分析法（ICA）、规范变量分析法（CVA）等。

核主元分析（Kernel Principal Component Analysis，KPCA）方法是一种非线性系统故障诊断方法，通过使用非线性映射技术，将输入空间映射到高维特征空间，再进行主元分析，获得有效的主元，在非线性故障诊断方面有着广阔的使用空间。核主元分析方法的原理与步骤具体如下：

假设一样本xi（i=1，2…，n，xt缀Rm），将样本映射到高维特征空间xi→准（xi）计算协方差矩阵[14~15]：

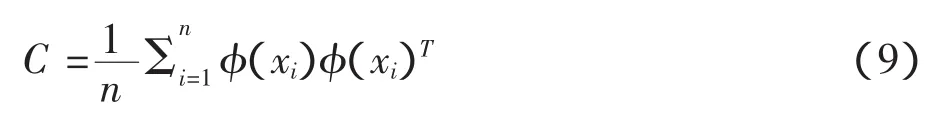
对矩阵C进行特征分解：

选择核函数k（xi，xj）=（准（xi），准（xj））,对于一个m维正常状态数据xi（i=1，2…，n，xt缀Rm）根据式：

计算X标准数据集的核矩阵K缀Rnxn。

对核矩阵归一化：

根据nλ =（ak，ak）=1 对特征向量进行归一化。

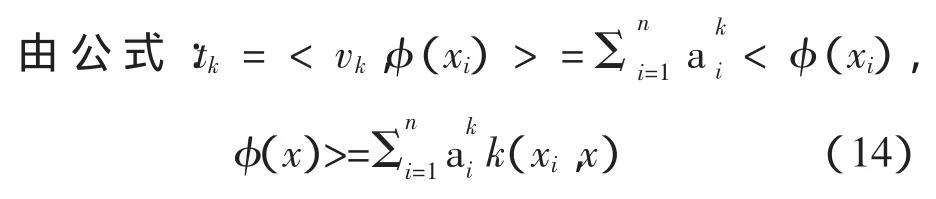
对正常数据提取非线性主元。

计算正常状态下数据集的T2和SPE统计量：

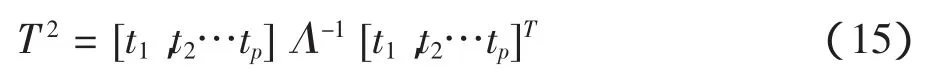
式中：[t1，t2…tp]是测试向量x的主元得分，Λ-1为主元特征值构成的对角逆矩阵，T2的置信限通过F分布获得：

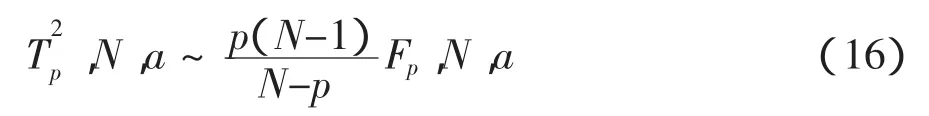
式中：N为样本数目；p为保留的主元个数。

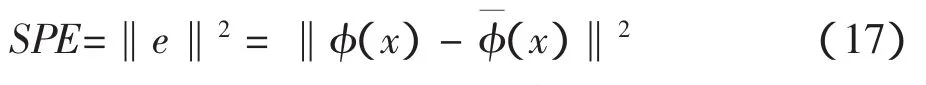
如果T2和SPE都小于预设阀值表明没有故障，否则表示发生故障。

2.2 基于交互式多模型的车辆悬挂系统故障诊断方法

交互式多模型算法 (Interacting Multiple-Model,IMM)最初应用于运动目标跟踪，是一种关于混合系统正态估计的次优算法。该算法设置了一个包含目标运行状态模型集M，每一种模型对应一个滤波器，各模型可以相互转化，相互转化服从马尔科夫过程，因其支持不同模型间的转化，所以在运动模型发生变化时表现出不错的目标跟踪效果。IMM算法包含四个步骤：模型间的交互，滤波器滤波，模型概率更新，数据融合。IMM算法具体流程图如图4所示。

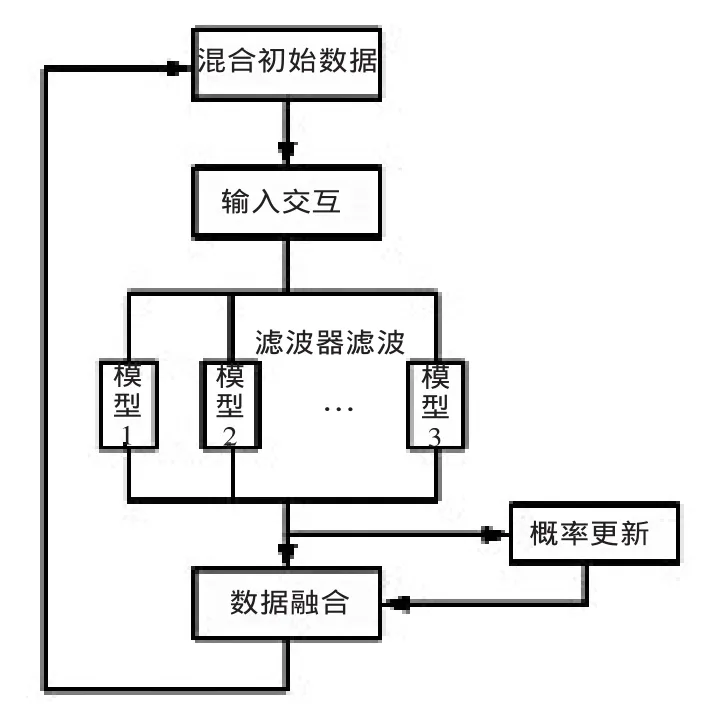
图4 IMM算法流程图

（1）模型间的交互

计算各对应模型的混合初始概率，各对应滤波器混合初始状态及协方差矩阵。

（2）滤波器滤波

在IMM中一般采用kalman filter算法来进行滤波和预测，根据交互后得到的混合初始状态和协方差矩阵进行卡尔曼滤波，滤波后得到各模型对应的子滤波器输出的目标状态估计值及协方差矩阵。

（3）模型概率更新

模型概率更新是IMM算法的关键环节，一般采用最大似然比函数法，获得不同模型输出结果。

（4）数据融合

将更新的概率和协方差矩阵进行融合获得新的状态估计值和协方差矩阵。

IMM算法的四个步骤完成标志一个递推周期结束，将本次融合数据作为下次的混合初始数据开始下一个递推过程。

2.3 基于多传感信息融合的车辆悬挂系统故障分离诊断方法

采用多传感信息融合技术对车辆悬挂系统进行故障诊断，就是通过对车辆悬挂系统进行动态分析，数学建模及建立悬挂系统故障类型库，使用EROS和D-S证据理论对故障类型进行分离，具体流程图如图5。

图5信息融合技术诊断流程图

2.3.1 车辆悬挂系统基于信息融合技术故障分离算法

基于信息融合技术故障诊断算法主要介绍D-S证据理论故障分离方法。车辆悬挂系统基于信息融合技术故障分离算法的过程：建立车辆悬挂系统数学模型，对车辆悬挂系统数学模型输出采用Kalman Filter产生残差，当故障发生时，对残差进行FFT运算，获得故障频域特征值，并与悬挂系统故障库中故障类型进行Eros相似性匹配得到信度函数，将信度函数用D-S证据理论进行融合，经过决策规则获取故障类型。

2.3.2 Eros（Extended Frobenius Norm）

计算两个多变量时间序列项（Multivariate time series，MTS）中的变量并根据结果判断最终相似度。从MTS子集库中分别选择矩阵A，B，并计算A，B的协方差矩阵MA，MB，对MA，MB进行奇异值分解[16]：

式中:VA=[a1…am]，ΣA=diag（λA1，λA2…λAm）

矩阵A，B的相似计算方程：

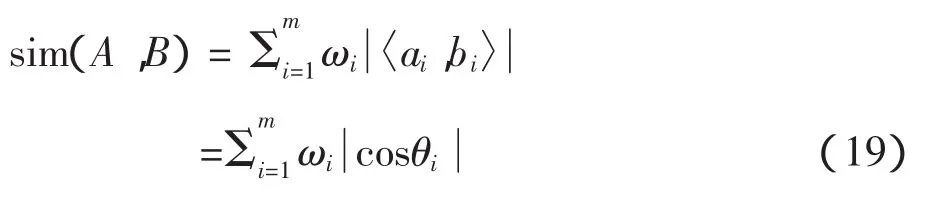
式中：〈ai，bi〉是向量ai，bi的内积；ω 是基于 MTS数据集特征值的权重，cosθi是向量ai，bi间的角度。

2.3.3 D-S证据理论联合与决策机制

基于D-S证据理论的联合规则[17]，假设m1，m2是识别框架Θ的两个信度函数分布，E1，E2，…EK是它们的各自焦元，则有：

式中：C代表证据源冲突的基本概率信度，证据源之间冲突越严重，C值越大。m（A）所有故障模型经过证据理论联合后的新信函数，证据理论联合满足一下规则关系：

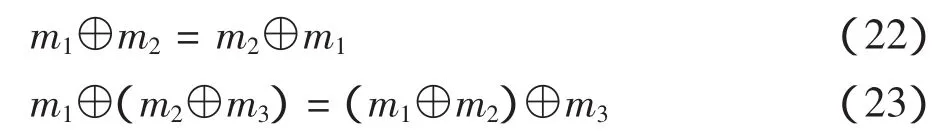
决策机制：（1）定有的目标类型应具备最大的信度函数分布。（2）目标类型和其他类型信度函数间的差距要大于一定的阀值。

3 轨道交通车辆故障诊断方法优化

目前国内外众多研究机构在轨道交通车辆悬挂系统故障诊断方面做了大量研究，并取得了一定的研究成果，也提出了一些行之有效的故障诊断方法，由于车辆悬挂系统的动力学特性在垂向和横向上具有耦合，悬挂系统部件的非线性，车体的柔性结构等因素的制约，车辆悬挂系统故障实时、准确、可靠地诊断仍任重道远。每一种对轨道车辆悬挂系统故障诊断方法并非完美，通过各种诊断方法的分析优化，对轨道车辆悬挂系统故障诊断研究有举足轻重的指导意义。

基于多元统计分析的车辆悬挂系统故障诊断方法在处理线性与非线性问题起着重要的作用，尤其是改进的基于核函数多元统计分析方法解决非线性的工程系统具有一定的优越性，但多元统计分析方法仅能诊断故障，不能判别故障类型；基于IMM的车辆悬挂系统故障诊断方法在运动目标跟踪和混合状态估计方面有着显著地优势，可综合考虑悬挂系统不同故障类型，提高故障诊断的精度；基于多传感信息融合的车辆悬挂系统故障分离诊断方法可提高目标识别的可靠度和鲁棒性增强数据的可信度，但Eros方法对低纬度的残差估算比较使用，当残差为高维度时，会造成计算量增加可信度下降，在线故障分离诊断比较难以实现等问题。通过对各种诊断方法的研究分析，可以取长抑短、优势互补，为今后车辆悬挂系统在线故障诊断提供新的思路和方法。

4 结束语

通过城市轨道交通车辆悬挂系统动态建模分析表明影响车辆悬挂系统动态因素较多，悬挂系统振动比较复杂，具有耦合性和非线性等特点，结合对车辆悬挂系统故障诊断多种方法分析优化，为日后车辆悬挂系统故障诊断提供了方法和指明了目标：

（1）探索和建立车辆悬挂系统非线性数学模型，能精确地反映车辆悬挂系统的运动特性。

（2）车辆悬挂系统故障诊断大部分停留在故障诊断报警技术层面，在对车辆悬挂系统故障分离诊断方面的研究比较薄弱。

（3）大部分车辆悬挂系统故障诊断研究还停留在理论研究，在实际应用较少。

[1]Yusuke Hayashi，Hitoshi Tsunashima,Yoshitaka Marumo.Fault detection of railway vehicles using multiple model approach[J].SICE-ICASE International Joint Conference，2006，（10）:18-21.

[2]Hitoshi Tsunashima,Hirotaka Mori.Condition Monitoring of Railway Vehicle Suspension Using Adaptive Multiple Model Approach[J]，International Conference on Control,Automation and Systems ，2010，（10）:27-30.

[3]Yue Wang，Zehui Mao，Bin Jiang.Observer-based fault detection for rail vehicle suspension systems[J].2014 26th Chinese Control and Decision Conference，2014:2863-2869.

[4]P.Li and R.Goodall.Model-based condition monitoring for railway vehicle systems[D].Master’s thesis，Control，University of Bath，Landon，UK，2004.

[5]Dae Sung Lee，Jong Moon Park，Peter A.vanrolleghem.Adaptive Multiscale Principal Component Analysis for On-line Monitoring of a Sequencing Batch Reactor[J].Journal of Biotechnology，2005，116(2):195-201.

[6]Xiukun Wei，Ying Guo，Limin Jia.MBPLS-Based Rail Vehicle Suspension System Fault Detection[J].2014 26th Chinese Control and Decision Conference，2014:3602-3607.

[7]Xiukun Wei，Ying Guo，Limin Jia.Fault detection of rail vehicle suspension system based on CPCA[J].2013Conference in Control and Fault-tolerant System，2013:9-11.

[8]Xiukun Wei，Kun Guo,Limin Jia.Fault isolation for light rail vehicle suspension system based on multi-sensor information fusion[J].2013 25th Chinese Control and Decision Conference，2013:3532-3537.

[9]XiukunWei，Hai Liu，Yong Qin.Fault Isolation of Rail Vehicle Suspension Systems by Using Similarity Measure[J].2011 23th Chinese Controland Decision Conference，2011:391-396.

[10]Xiukun Wei， Limin Jia， Hai Liu.Data-Driven Fault Detection of Vertical Rail Vehicle Suspension Systems[J].UKACC International Conference on Control 2012,2012(7)：589-594.

[11]方 宇，陈 龙，郑树彬.基于参数估计的轨道车辆悬挂系统状态监测方法[J]Journal of The China Railway Socirty，2013，(5):15-20.

[12]Lennart Ljung.Asymptotic Behavior of the Extended Kalman Filter as a Parameter Estimator For Linear Systems[J].The Transcations on Automatic Control，1979:36-50.

[13]Yue Wang，Zehui Mao，Bin Jiang.observer-based fault detection for rail vehicle suspension systems[J].2014 26th Chinese Control and Decision Conference，2014:2863-2869.

[14]毕小龙.基于核主元分析的传感器故障检测[J].动力工程，2007，(4):555-559.

[15]Li Xuemei，Shao Ming，Ding Lixing.A novel HVAC Fan Machinery Fault Diagnosis Method Based on KPCA and SVM[J].2009 International Conference on Industrial Mechatronics and Automation，2009:492-496.

[16]杨 静，田 亮，赵爱军.基于典型样本的证据理论信度函数分配构造方法[J].华北电力大学学报，2008，(9):71-73.

[17]Zhou Yulan，Zang Yanhong，Lin Yahong.Based on Multi-sensor Information Fusion Algorithm of TPMS Research[J].2012 International Conference on Solid State Devices and Materials Science，2012:786-792.