全站仪坐标测量精度评定方法探讨
张前恩,李 斌,杨 凡 ,苏 杰
(1.61287部队,四川 成都610000;2.信息工程大学,河南 郑州 450001)
在当前的大尺寸工业测量领域,坐标测量是最常见的测量工作,比如航空航天的大型设备拼接测量、制造业的形位检测、大型精密工程的定位安装测量等,而全站仪是最主要的测量仪器[1-5]。这些三维测量工作,无论是定姿定位、静态或者动态,其实质都是要求高精度的点位坐标测量[6]。
当前,全站仪的标称精度指标几乎都以测角精度和测距精度分别给出[7-10],将其应用于三维测量面临2个问题:①现有的精度指标不能直观表明其坐标测量在理论上可以达到的精度值;②用测角和测距指标来衡量全站仪量程内的坐标测量精度,国内外缺乏相应规范。以上2个问题决定了对全站仪实际的坐标测量精度缺乏定量认识,那么,具体工程测量的精度评估就缺乏理论依据,测量方案的可行性也就得不到有力支撑。
在全站仪三维测量领域,坐标测量精度的检定方法以及制定相应的行业规范将是必然的发展趋势。激光跟踪仪就是典型的例子,其精度指标就直接给出量程内理论上可以达到的坐标精度[10,11],而不再分别给出角度和距离精度,比如Leica AT901在80 m范围内为±(15 μm+6 μm/m)。因此,对全站仪坐标测量精度的评估方法研究是十分必要的。
1 高精度检校场的建立
激光跟踪仪采用干涉法测距,是当前精度最高的移动式坐标测量系统,基于极坐标原理获取高精度角度和距离观测值,转化得到点坐标,其点位精度能达到μm量级。基本思路是利用激光跟踪仪测量空间不同位置的若干固定点坐标,建立高精度空间坐标基准。
1.1 检校场设计
检校场选择建立在20 m×10 m×5 m的稳定空间内,要求布设于空间不同位置的控制点可无障碍通视。
1)控制点布设。控制点由CCR1.5"球棱镜和靶座组成,靶座通过螺栓固定用于保存点坐标。控制点在空间水平和垂直方向均匀布设,命名为Pi,i=1,…,15,如图1所示。

图1 检校场空间设计
2)强制对中墩。为了保证全站仪设站的稳定性,在空间内建立强制对中墩5个,命名为F0~F5,其中F3、F0和F1基本共线,F4、F0和F2基本共线。
1.2 检校场基准测量
采用Leica AT901-B激光跟踪仪进行检校场坐标基准测量,该仪器点位测量标称坐标精度为± (15 μm+6 μm/m)。激光跟踪仪对设站位置没有严格要求,考虑到空间点图形结构对测量精度的影响,将AT901-B建站于空间点中心位置(F0旁边)。
1.3 检校场精度评定
为了评定检校场基准测量精度,将激光跟踪仪分别于2个位置设站,测量控制点三维坐标。基于最小二乘坐标转换模型处理数据,得到点位精度dp,如图2所示。可以看出,点位误差在区间[0.012,0.219]内,点位中误差RMS=0.087 mm。排除2个粗差点P4和P12后的点位精度为dp2,RMS=0.062 mm。
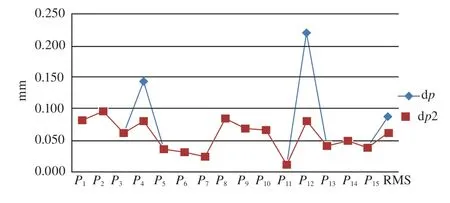
图2 检校场基准测量点位精度
2 加常数测定
加常数C是全站仪与CCR1.5"球棱镜的测距常数[12],该值因仪器和棱镜而异,需要测定并进行改正。
2.1 测定方法
由于强制对中墩稳定性较好,且不存在对中误差,因此可利用对中墩基于三段法测定加常数,原理如图3所示。
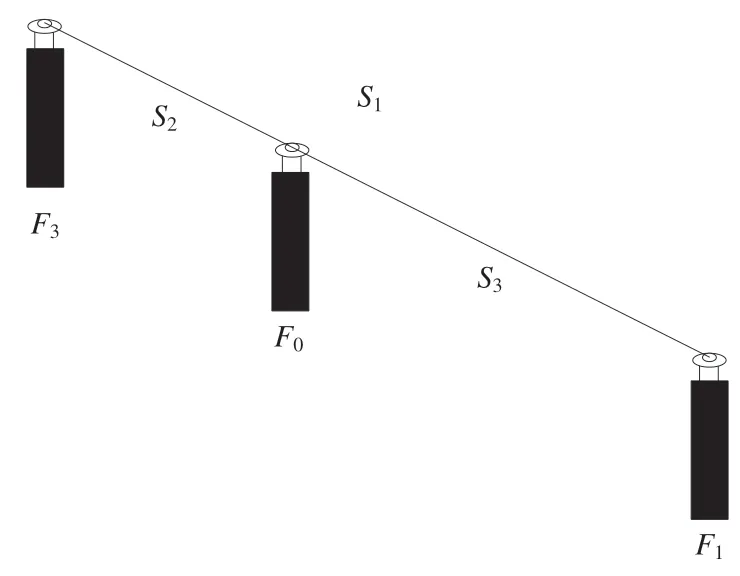
图3 加常数测定
当对中墩F3、F0和F1共线时,加常数与平距S1、S2和S3满足如下关系:

2.2 不共线的误差评估
当对中墩F3、F0和F1不严格共线时,则式(1)不成立。其不共线对加常数C的影响可以通过三角形余弦定理进行评估。经测定,F0F1与F0F3两条边的夹角为179°58'13",由三角形余弦定理可以求解S1的实际长度S1':

以TS30测量值为例,S1=6.909 0 m;S2=12.451 3 m,计算得到的长度值S1'=19.360 299 m,不考虑不共线影响的长度值S1=S2+S2=19.360 3 m,二者差值为0.6 μm,可以看出不共线对C值的影响可以忽略。
3 坐标精度评定
全站仪的坐标精度基于最小二乘坐标转换模型来解算。常见的坐标转换模型较多,其中,基于四元数的解算模型具有抗奇异性、表单简洁和易于实现等特点。
3.1 坐标系转换模型
在四元数模型中,旋转矩阵R有如下表达式[13,14]:

平移矩阵T的表达式为:

列向量q*=(q0qx qy qz)T为单位四元数,满足条件:

假设两坐标系点集的质心分别表示为p和q,其表达式为:

式中,设反对称矩阵A=Σ−ΣT;列矢Δ=(A23A31A12)T;对称矩阵Q的表达式为:

解算矩阵Q的最大特征值,其对应的特征向量就是四元数 。
3.2 内符合精度
全站仪在3个对中墩F3、F0和F1上分别设站观测,记录控制点三维坐标。剔除粗差值,基于四元数的最小二乘模型计算坐标转换精度,以TDA5005、TS30和MS05A为例,坐标内符合精度计算结果如表1、图4~6所示。

表1 全站仪内符合精度

图4 TDA5005坐标内符合精度

图5 MS05A坐标内符合精度

图6 TS30坐标内符合精度
3.3 外符合精度
将全站仪坐标测量值与激光跟踪仪坐标测量基准值比较,可以得到全站仪的坐标测量绝对精度,即外符合精度,如图7~9所示。

图7 TDA5005外符合精度

图8 MS05A外符合精度
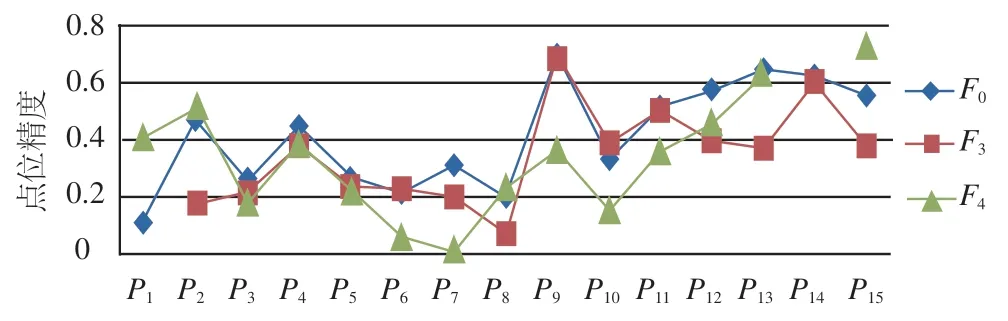
图9 TS30外符合精度
4 绝对长度基准测量
加工膨胀系数极小的碳纤维基准尺,经双频干涉仪检定为1 446.30 mm。距仪器一定距离处摆放基准尺,分别测量4种姿态下的基准尺长度,如图10所示。通过对绝对长度的测量,直观反映全站仪的坐标测量精度。各仪器所测基准尺长度与检定值的偏差如表2所示。

图10 基准尺测量

表2 基准尺测量结果
5 结 语
建立了一套完整的全站仪坐标测量精度评估方法,包括高精度检校场的建立、绝对精度与相对精度的评定方法、基准尺测量等内容,并以TDA5005、TS30和MS05A 3种工业全站仪为例进行坐标测量精度的评定,取得了良好效果。
[1]周红进,许江宁,马恒,等.GPS与全站仪组合测量载体航向模型研究[J].武汉大学学报:信息科学版, 2005,30(6):510-513
[2]周西振,尹任祥.侧边后方交会精度研究及其应用[J].西南交通大学学报, 2006,41(3):344-348
[3]范百兴.激光跟踪仪高精度坐标测量技术研究与实现[D].郑州:信息工程大学, 2013
[4]张春富.基于激光跟踪仪的固体火箭发动机推力线测量技术研究[D].哈尔滨:哈尔滨工业大学, 2007
[5]欧阳健飞,刘万里,闫勇刚,等.激光跟踪仪坐标测量精度的研究[J].红外与激光工程, 2008,37(增刊):15-18
[6]JJF 1242-2010.激光跟踪三维坐标测量系统校准规范[S].
[7]黄桂平,叶声华,李广云.经纬仪大尺寸柔性三坐标测量系统的开发与应用[J].仪器仪表学报, 2002,23(3): 607-610
[8]李杏华,张国雄,赵树忠,等.跟踪机构精度检测的研究[J].计量技术, 2009(5):7-9
[9]王彦.激光跟踪仪测量系统校准技术研究[J].测试技术,2003(3): 37-41
[10]李广云.LTD500激光跟踪测量系统原理及应用[J].测绘工程, 2001,10(4): 3-8
[11]JJG100-94.全站型电子速测仪检定规程[S].
[12]Mark J.Status Report on the Survey and Alignment Activities at CERN[C].KEK,2008
[13]Lau K, Hocken R J.A Survey of Current Robot Metrology Methods[J].Annals of the CIRP,1984, 33(2): 485
[14]Lau K,Hocken R J,Haight W C.Automatic Laser Tracking Interferometer System for Robot Metroloty[J].Precision Engineering, 1986, 8(1): 3-8

