基于因散经验模式分解与最小二乘支持向量机的风电场短期风速预测

杨德友，蔡国伟

(东北电力大学电气工程学院，吉林吉林132012)

风能作为一种无污染的环境友好型能源，已经成为世界各国争相发展的新能源，并得到了快速的发展［1－3］。风电机组以自然风为原动力，自然风的间歇性和不确定性决定了风电场出力具有较强的随机性。随着风电并网规模的不断增大，风电场有功输出的不确定性和不可控性给电网的安全稳定运行带来了巨大的挑战。风速预测作为解决上述问题的有效手段，近年来得到了广泛的关注。准确的风速预测结果可以为规划和调度提供有力的依据，也已成为大规模风电并网后能量管理系统(EMS)中不可或缺的重要组成部分［4－5］。

目前，国内外风速预测的方法主要有时间序列法［6］、统计学方法［7］、人工智能法［8－9］以及以信号分析为基础的预测法［10－11］等。由于风速受温度、气压等环境因素的影响较大，且随机性和间歇性较强，这就使得传统的时间序列和统计学方法在短期风速预测中的应用受到了一定的局限。神经网络及支持向量机等人工智能方法对于具有良好周期性的数据具有较高的预测精度，但对于具有强随机性的风速数据，其预测精度仍不够理想。现代信号分析方法的引入为短期风速预测开辟了新的途径，现有文献中应用的信号分析方法主要有小波分析和经验模式分解(EMD)。经验模式分解在一定程度上解决了小波分解受人为因素影响大，小波基选取困难等问题，但对于含噪声分贝较高的数据，经验模式分解会出现混频现象，影响分解效果，不利于掌握原有物理数据的周期特性。因散经验模式分解(EEMD)通过噪声辅助对实测风速数据进行分析，可以减弱混频现象对分析结果的影响，进一步改善分析效果。

基于上述分析，本文结合因散经验模式分解和最小二乘支持向量机建立了综合考虑温度和气压因素的短期风速预测模型。首先利用因散经验模式分解对历史风速数据进行分解得到若干具有周期性的本征模态分量，进而利用最小二乘支持向量机对各本征模态分量进行预测，最后将所得结果重构即可得到风速预测结果。两组不同地区风速预测结果表明本文提出的算法具有较高的精度且适应性较强。

1 因散经验模式分解(EEMD)

1.1 EEMD的基本原理及分解过程

经验模式分解(EMD)是由Huang N E在1998年提出的Hilbert－Huang变换中的重要部分［12］。近年来在诸多领域得到了广泛的应用，效果显著。但文献大量实验数据研究表明［13］，当数据不是纯白噪声时，EMD分解会出现频率混迭现象。而实测数据中都不同程度融合了信号和噪声，这就使得EMD分解的混频现象难以避免，这也是原始EMD方法的主要不足之一。为了弥补原始EEMD方法的不足，Z.Wu和N.E.Huang在2005年提出了因散经验模式分解法(EEMD)［13－14］。该方法是一种新的噪声辅助数据分析方法，其主导思想是认为每个观察到的数据都融合了实际的时间序列信息和噪声，即使同一过程数据被不同的人收集得到，也具有不同的噪声水平，但其整体均值接近于真实的时间序列，EEMD分解具体过程见文献［13］。

图1 测试信号及其组成分量

1.2 测试信号分析

为了对比EMD和EEMD对含噪信号的分解效果，构造式(1)所示信号，并加入20 dB的白噪声，如图1所示。其中，图1中信号 x1、x2、y、yp分别对应于式(1b)、(1c)、(1a)及(1a)加入20 dB白噪声的结果。

图2

对测试信号分别利用EEMD和EMD进行分解，所得结果如图2(a)和图2(b)所示。同时计算得到imf4和imf5的瞬时频率，如图3所示。从图2(a)、(b)以及瞬时频率计算结果不难看出，与EMD相比，EEMD分解结果频率更加平稳，能够更好的反映原始信号的物理特性，而EEMD的这种特点使其更适用于对随机性较强风速数据进行分解，继而得到能够真实反映风速周期特性的本征模态分量。

图3 imf4及imf5瞬时频率计算结果

2 支持向量机

支持向量机(support vector machines，SVMs)是Vapnik等人在现代统计学习理论基础上提出的一种新的学习方法［15］，具有结构简单、全局最优、泛化能力好的优点，近几年得到了广泛的研究。

对于给定的n维训练样本，{xi，yi}(i=1，2，...n)∈Rn×R，支持向量机的线性回归函数可以表示为:

依据SRM准则，同时考虑正规化项和拟合误差平方和，可以将回归问题转化为如下所示的有约束且存在唯一解的二次规划问题。

式中，γ为可调参数。

为了求解上述优化问题，引入拉格朗日函数将有约束优化问题转化为无约束优化问题:

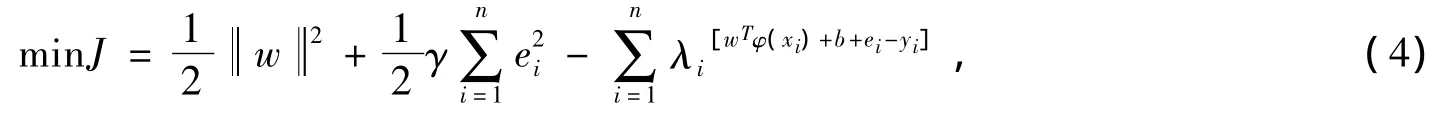
根据KKT(Karush－Kuhn－Tucker)条件，可得到如下线性方程组:

利用最小二乘法求解式(5)的线性方程组，从而解出b和λ，最后得到LS－SVM回归函数［16］

支持向量回归适合于进行非线性数据处理，在预测方面具有较强的泛化推广能力，且具有全局最优解，因此，本文采用支持向量回归建立每个本征模式分量的预测模型。

3 预测模型的建立

通过上述分析和论述，本文建立了如图4所示的风速预测模型。

上述预测模型预测过程可以分为以下几个步骤:

(1)利用EEMD将历史风速数据进行分解，得到周期性相对平稳的imf分量;

(2)将各imf分量数据和温度、气压数据进行归一化处理后作为支持向量机的输入;

(3)利用归一化后数据对各支持向量机模型进行训练;

(4)利用训练好的支持向量机模型对后续24小时风速进行预测。

图4 基于EEMD及LS_SVM预测的模型

4 实例分析

4.1 风速数据的EEMD分解

本文选用香港某风场2000年1月份每1小时记录一次的风速数据，按时间顺序选用连续336个观测点作为训练数据，其后24点数据作为测试样本。利用Matlab2009a进行编程实现图4所示预测模型。

首先，分别利用EMD及EEMD对连续两周(即336点)数据进行分解得到如图5(a)及图5(b)所示的分解结果。对比EEMD和EMD的分解结果不难看出，EEMD分解所得的本征模态分量数目要多于EMD的分解结果。同时对比图5(a)及图5(b)不难发现，EEMD分解得到的本征模态分量数目为7个，而EMD分解的到的本征模态分量个数为5个，表明EEMD分解能够在一定程度上解决EMD分解结果存在的模态混叠现象，其分解结果的平稳性要明显优于EMD的分解结果，这种平稳性在一定程度上可以提高预测精度。

图5 风速分解结果

4.2 预测模型参数选取及预测误差分析

在各个imf分量进行预测时，本文选用回归预测中最为常用的核函数——径向基函数作为核函数:

同时为方便计算参数设定为σ =0.05，γ=100。

选用科学且合理的误差指标，对评价预测模型的有效性具有十分重要的意义。本文选用式(8)、(9)绝对百分误差(Ape)及平均绝对百分误差(Mape)作为性能指标。

式中:Sr为原始风速值;Sf为预测风速值;N为预测样本数。

为了选取合理的训练样本，本文首先利用建立的预测模型分别对训练样本为168个(1周)、336个(2周)及504个(3周)三种情况进行了计算及误差统计，结果如表1所示。由表中计算结果可以看出，随着训练样本数目的增加，预测精度均有不同程度的增加，但训练样本数目的增加在提高预测精度的同时也增大了计算量，训练时间变得更长。大量的计算结果表明，336个(2周)训练样本的计算结果精度在满足工程需要的同时，计算量适中，因此，本文计算过程中训练样本数选用连续两周的风速数据，

表1 样本数对预测结果影响统计结果

在利用本文提出的预测模型对训练数据后续24小时风速进行预测的同时，本文也利用EMDSVM模型以及单一SVM对后续24小时风速数据进行了预测，预测结果与实际数据对比如图6所示。各方法对应的绝对百分误差对比如图7所示。

图6 预测结果对比图

图7 预测误差对比图

对三种方法计算结果的误差进行统计后，得到如表2所示的统计结果。从表2的统计结果可以看出，本文提出的预测模型的平均误差为6.99%，最大误差和最小误差分别为20.62%和0.75%，三项误差统计指标均优于EMD－SVM和单一SVM模型，预测精度相对较高。

表2 预测误差统计结果

5 结 论

准确的风速预测结果是大规模风电并网后保证电力系统安全稳定运行的重要基础。本文基于因散经验模式分解(EEMD)和最小二乘支持向量机(LS_SVM)建立了计及温度和气压因素的风速预测模型。仿真分析及对实际风速数据的计算和分析表明:

(1)EEMD可以有效解决原始EMD分解的混频现象，利用EEMD分解得到本征分量频率相对EMD的分解结果更加平稳;

(2)本文提出的预测模型可以同时考虑温度和气压等环境因素;

(3)本文模型预测精度明显优于EMD－SVM和单一SVM模型且学习效率较高。

［1］雷亚洲.与风电并网相关的研究课题［J］.电力系统自动化，2003，27(8):84－89.

［2］FanShu，Liao J R，Yokoyama R，et al.Forecasting the wind generation using a two－stage network based on meteorological information［J］.IEEE Transactions on Energy Conversion，2009，24(2):474－482.

［3］World Wind Energy Association.Wind turbines generate more than 1%of the global electricity［EB/OL］.(2008－02－21)［2008－03－20］.http://www.windea.org.

［4］雷亚洲，王伟胜，戴慧珠，等.风电对电力系统运行的价值分析［J］.电网技术，2002，26(5):10－14.

［5］杨秀媛，肖洋，陈树勇.风电场风速和发电功率预测研究［J］.中国电机工程学报，2005，25(11):1－5.

［6］王健，严干贵，宋薇，等.风电功率预测技术综述［J］.东北电力大学学报，2011，31(3):20－24.

［7］蔡凯，谭伦农，李春林，等.时间序列与神经网络法相结合的短期风速预测［J］.电网技术，2008，32(8):82－90.

［8］李智，韩学山，韩力，等.地区电网风电场功率超短期预测方法［J］.电力系统自动化，2010，34(7):90－94.

［9］范高锋，王伟胜，刘纯，等.基于人工神经网络的风电功率预测.中国电机工程学报，2008，28(34):72－76.

［10］王晓兰，王明伟.基于小波分解和最小二乘支持向量机的短期风速预测［J］.电网技术，2010，34(1):179－184.

［11］刘兴杰，米增强，杨奇逊.一种基于EMD的短期风速多步预测方法［J］.电工技术学报，2010，25(4):165－170.

［12］N.E.Huang，S.R.Long，M.C.Wu，H.H.Shi，Q.Zheng，N.C.Yen，C.C.Tung，and H.H.Liu，The empirical mode decomposition and the Hilbert spectrum for nonlinear and non－stationary time series analysis［J］.Proceedings of the Royal Society A:Mathematical，Physical and Engineering Sciences 454，1998，454(2):903－995.

［13］游子跃，王宁，李明明，等.基于 EEMD和 BP神经网络的风机齿轮箱故障诊断方法［J］.东北电力大学学报，2015，35(5):64－72.

［14］V.N.Vapnik.The Nature of Statistical Learning Theory［M］.New York:Springer－Verlag，1995.

［15］聂鹏，宋坤，田莉，等.基于支持向量机的城市电网空间负荷预测方法［J］.东北电力大学学报，2014，34(4):28－33.

［16］A.K.Johan，et al.Least Squares Support Vector Machines［M］.NJ:World Scientific，2002.