含分布式风电和储能的配网潮流计算方法研究

吴 彤，陈洪涛，赵建明，李国庆

(1.东北电力大学电气工程学院，吉林吉林132012;2.国网吉林省电力有限公司松原供电公司，吉林松原138000)

随着分布式风电电源和储能装置在电网中渗透率的增加，使得配电网从传统的辐射状网络转变为多电源供电模式，进而改变了配电系统的结构和运行模式，这无疑会对配电网的电压分布、潮流走向等方面产生影响［1－3］。由于传统潮流计算算法无法对分布式电源进行处理，国内外研究学者开始着手研究更高效、实用的方法来满足复杂配电网快速计算和分析的需求。

文献［4］提出了一种基于回路分析法的简化潮流计算方法，将回路电压方程转化为线性代数方程进行求解;文献［5］对网络中PV节点进行优化，进而提高潮流计算效率;文献［6］采用改进的前推回代法进行含分布式电源的配电网潮流计算。这些计算方法都是对传统的潮流算法进行改进，使其能够更好的满足电网发展的需求，但在计算过程中都忽略了储能装置对潮流计算结果的影响。

为此，本文提出了一种简化实用的潮流计算方法，在综合考虑风电随机性和储能装置双向潮流特性的基础上，对传统潮流计算方法加以改进，使潮流计算的迭代次数更少，收敛效果更好。

1 风力发电机随机出力模型

1.1 风力发电机模型

目前风速模型普遍采用Weibull分布，其概率密度函数为

式中:v为风速;α为形状参数;β为尺度参数。

风力发电机的出力与风速的关系基本服从图1所示的出力曲线。图中:vci为切入风速;vr为额定风速;vco为切出风速;Pr为风机额定输出功率。

图1 风力发电机出力与风速关系曲线

如采用异步发电机，则风力发电机的简化等值电路如图2所示。由图中关系可推导出风力发电机的机端电压表达式和无功功率表达式。

式中:R2为转子电阻;X为定、转子电抗之和;Xm为励磁电抗;Xc为机端补偿电容电抗;s为转差率。

在风速一定的条件下，风力发电机的有功出力可视为固定值，则风力发电机的无功输出仅与转差率和机端电压有关。根据公式(2)和公式(3)消去转差率s即可得出无功与电压的关系Q=f(U)为:

式中，各变量含义与公式(2)－(3)中所给出的变量含义相同。

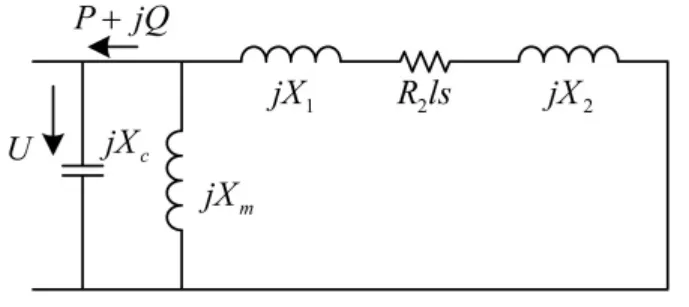
图2 异步发电机简化等值电路

1.2 风机出力概率分布情况

将风速概率密度函数带入风机出力表达式即可得到风机出力Pw的概率表达式［7］。

(1)Pw=0时，0 ＜ v≤vci∪v＞vco。

则有零出力情况下风机出力概率为:

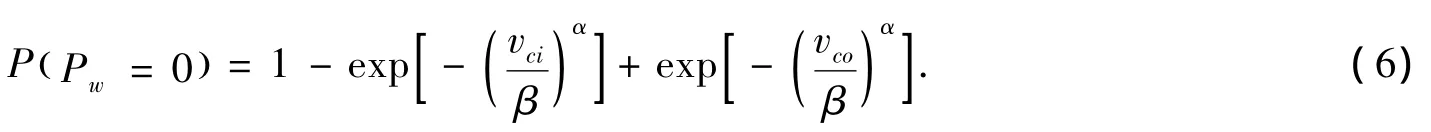
(2)0＜Pw＜Pr时vci＜v＜vr，第k段概率为

概率密度函数可由式(7)得到

欠出力离散段风机出力Pk采用该段有功出力的中间值，即期望值。

(3)Pw=Pr时，vr＜ v≤ vco。

在式(4)－(8)中，v为风速;α为形状参数;β为尺度参数;vci为切入风速;vr为额定风速;vco为切出风速;Pr为风机额定输出功率。

2 潮流计算中风机和储能节点的处理

2.1 潮流计算中风机节点的处理

由于异步风力发电机组并网点无功需同时满足公式(4)和潮流方程，如果只将其处理成一个简单的PQ节点进行潮流计算会与实际情况相差较大。为此，本文采用如下处理方法将风机出力看成一个输出无功随电压变化的PQ(V)节点，方法如下:

对于双馈式和直驱式风机，由于其机组电压相对稳定且对系统无功需求较小，故在潮流计算中可将其视为PV节点。

2.2 潮流计算中储能节点的处理

对于储能装置在电网中既可作为负载储存电能，又可以作为分布式电源向电网供电。当工作在整流状态时，储能装置处于充电状态，能量从电网侧流向直流侧;当工作在逆变状态时，储能装置处于放电状态，将直流侧的能量回馈给电网。当储能装置采用电流型逆变器时，做PI节点处理;采用电压控制逆变器时，做PV节点处理，本文所采用的储能装置选用电压控制逆变器。［8－10］

另外，由于储能装置容量受限，不可能一直处于充电或者放电状态，故需要相应的控制策略来实现其自动充放电功能。

2.3 储能装置控制策略

为确保电网能够稳定、可靠运行，储能装置必须依照一定的控制策略进行充放电。本文储能装置控制策略的数学模型如下:

式中:P(t－1)为风力发电机在t－1时刻平抑后的输出的功率;Pmax(t)、P(t)分别为t时刻输出的最大输出功率和平抑后的值;Pess(t)为储能装置的充放电功率;S、λ分别为装机容量和允许的输出功率的最大变化率。若Pess(t)＞0，则储能装置放电;若Pess(t)＜0，则储能装置充电。

也就是说，当风电输出的有功功率波动值大于其允许的最大波动值时，系统中会有能量剩余，此时将多余的能量送至储能装置进行充电，当储能装置充满后，停止充电，剩余的有功功率按照能源不浪费原则输出;当风电输出的有功功率波动值小于其允许的最小波动值时，系统中会产生功率缺额，此时储能装置进行放电，当储能装置电量放尽后，下一时刻开始不再放电。

3 潮流算法的实现

(1)读取原始数据，设定电压初始值。

(2)根据风力发电出力的概率分布和储能装置的控制策略确定系统最具代表性时刻，以此时刻下风机出力和储能装置的带电状态为初始状态。

(3)判定系统中节点类型，将风力发电机节点转化为PQ节点，将储能节点转化为PV节点，判断储能节点是否存在无功越限的情况。若出现无功越限，将储能节点转化为PQ节点参与潮流计算;若无功没有越限，将储能节点以PV节点参与潮流计算。

(4)由线路末端电流和功率前推计算各节点电流、功率。

(5)以平衡节点电压回代计算线路末端节点电压。

(6)计算系统中PV节点相邻两次迭代电压的差值，若满足精度，则结束潮流计算。

4 仿真验证

4.1 系统基本资料

本文在Matlab环境下进行程序编译来实现文中所提出的潮流计算方法，并采用PSAT(Power System Analysis Toolbox)搭建仿真模型，通过潮流计算结果对比来验证本文所提算法的有效性。

以IEEE33节点系统为例，系统电压基准值为12.66 kV，视在功率基准值为10 MVA。系统中包含4台额定功率为300 kW的风机和一额定容量为480 kW·h的储能蓄电池。其中1节点为平衡节点，风机接入节点分别为7节点、14节点、25节点和32节点，储能接入节点为11节点。仿真模型如图3所示:

图3 IEEE33节点测试系统仿真模型

其中，风机的额定电压为0.69 kV，经0.69/12.66变压器与配电网相连，储能装置初始化处理为恒定PV节点，但同时受控制策略限制其进行充放电。

4.2 仿真计算结果

采用Matlab编程进行计算，将计算所得结果与PSAT潮流计算结果进行对比，结果如表1所示。

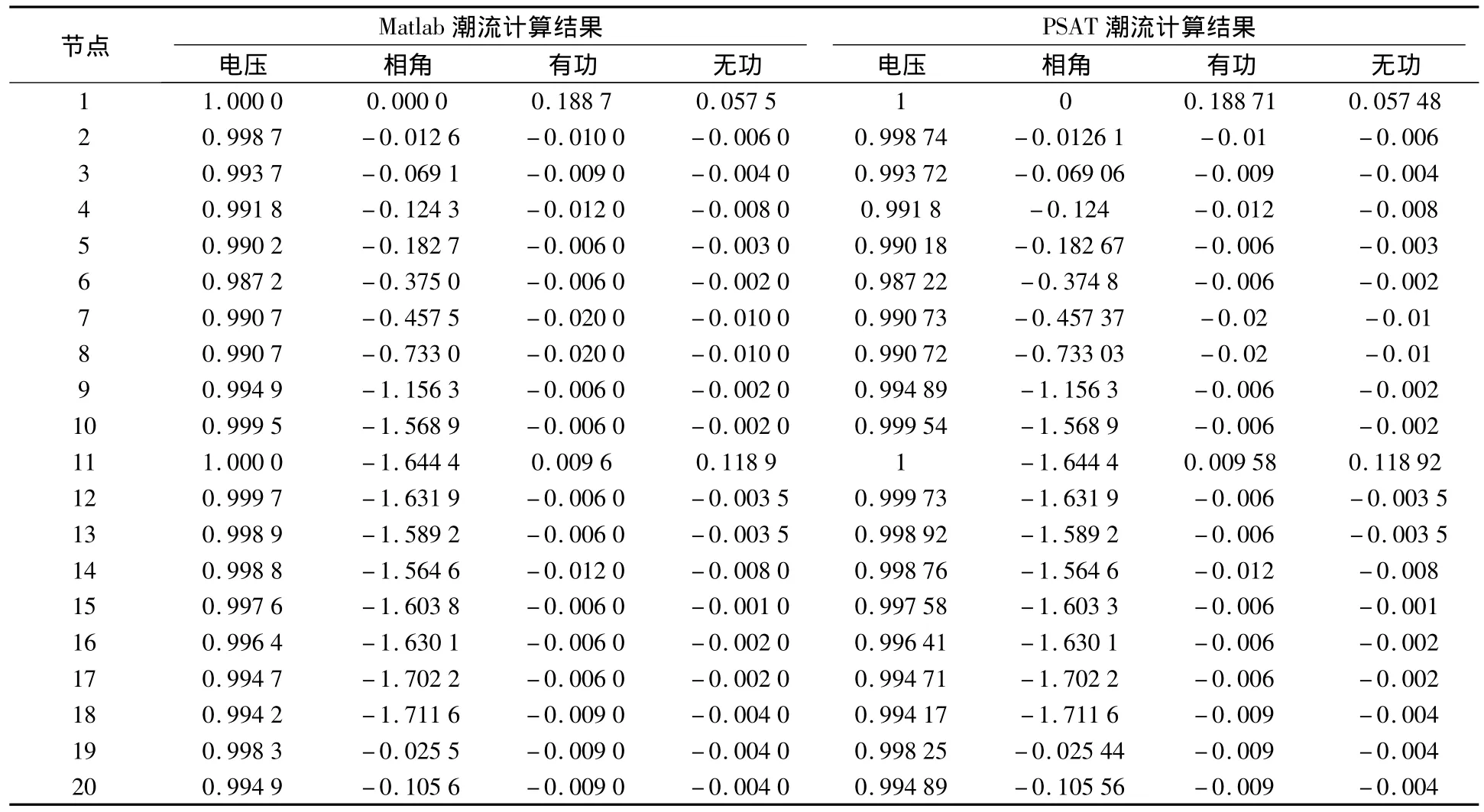
表1 Matlab编程与PSAT仿真结果对比

由表1中数据对比可以看出，经Matlab编程求得的各节点电压与PSAT仿真模型求得的节点电压基本相同，且误差在允许范围内。说明本文提出的潮流计算方法可以有效的对含分布式风电和储能装置的配电网进行潮流计算。

5 结 论

本文根据风机出力特性和储能装置的双向潮流特性，提出了一种简化的潮流计算方法，用于解决传统潮流计算方法不能处理分布式风电和储能装置的问题。采用Matlab编程来实现本文所提出的潮流计算方法，并以PSAT工具箱计算的结果进行对比，结果表明，本文所提出的潮流计算方法可以有效对含分布式风电和储能装置的配电网进行潮流计算。

［1］孔瑾.智能配电网的电网分区及孤岛辨识研究［D］.山东:山东大学，2013.

［2］杨华，吴政球，涂有庆，等.分布式发电及其并网技术综述［J］.电网技术，2008，32(15):71－76.

［3］莫颖涛.影响我国分布式发电发展的关键因素［J］.电网技术，200832(S1):176－178.

［4］牛焕娜，井天军，李汉成，等.基于回路分析的含分布式电源配电网简化潮流计算［J］.电网技术，2013，37(4):1032－1038.

［5］杨超，沈聪，李睿.含分布式电源配电网的前推回代潮流算法中PV节点处理方法［J］.电网技术，2012，36(9):238－243.

［6］王建勋，吕群芳，刘会金，等.含分布式电源的配电网潮流快速直接算法［J］.电力自动化设备，2011，31(2):17－21.

［7］马瑞，蒋斌.含风电场并考虑风速随机性的电力系统电压控制区域划分［J］.长沙理工大学学报，2008，5(3):71－76.

［8］Anju G Pillai，Thomas P C，Sreerenjini K，et al.Transient Stability Analysis of Wind Integrated Power Systems with Storage Using Central Area Controller［J］.2013 Annual International Conference on Emerging Research Areas and 2013 International conference on Microelectronics.2013:1－5.

［9］S Pérez－Londno，L Rodriguez－Garcia，Y Ulianov López.Effects of Doubly Fed Wind Generators on Voltage Stability of Power Systems［J］.2012 Sixth IEEE/PES Transmission and Distribution:Latin America Conference and Exposition(T＆D－LA).2012:1－6.

［10］陈厚合，吕志远，朱景明.基于混合连续蚁群算法的最优潮流研究［J］.东北电力大学学报，2009，29(6):54－59.