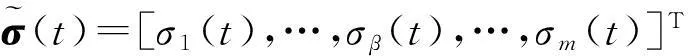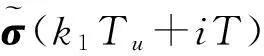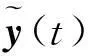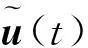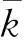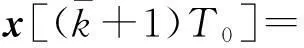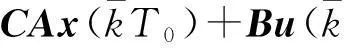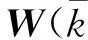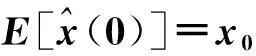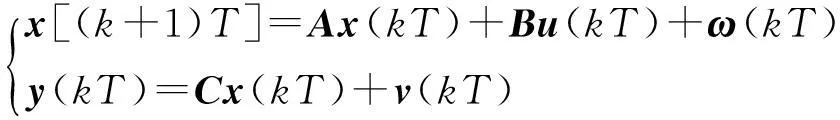具有通信约束的网络化控制系统LQG控制器设计

邵奇可，解　洋，张　江，洑佳红

(浙江工业大学 计算机科学与技术学院，浙江 杭州 310023)

具有通信约束的网络化控制系统LQG控制器设计

邵奇可，解洋，张江，洑佳红

(浙江工业大学 计算机科学与技术学院，浙江 杭州 310023)

摘要：针对一类具有噪声影响的通信受限多输入、多输出网络控制系统，利用非均匀采样方式将其建模为一类集控制与调度为一体的网络化控制模型，根据卡尔曼滤波器思想设计了最优状态估计器和最优保性能输出反馈控制器并在此基础上给出系统渐近稳定的充分条件.通过仿真验证了所提算法的可行性.该设计方法特别适用于通信受限情况下，系统存在多种信号类型时，可方便的根据不同信号特征设置系统的采样周期和调度周期，从而克服原离散周期性时变系统的控制器受通信序列周期性约束问题，避免多个控制器周期性切换，增加控制系统设计的自由度，提高系统动态重构能力和整体性能.

关键词：网络控制系统；通信受限；线性矩阵不等式；卡尔曼滤波；LQG最优控制

中图分类号：TP273

文献标志码：A

文章编号：1006-4303(2015)01-0103-07

LQG controller design for networked control systems with

communication constraints

SHAO Qike, XIE Yang, ZHANG Jiang, FU Jiahong

(College of Computer Science and Technology, Zhejiang University of Technology, Hangzhou 310023, China)

Abstract:The problem of LQG controller design for a class of MIMO networked control systems (NCSs) with limited communication and noise is studied in this paper. Firstly, a new network control model for the integration of control and scheduling is established by using non-uniform sampling method. Secondly, according to the design method of the Kalman filtering, an optimal state estimator based on the output value and the corresponding optimal guaranteed cost output feedback controller is proposed. An sufficient condition for asymptotic stability of the system is given. Finally, the simulation verifies the feasibility of the proposed algorithm.The design method is particularly applicable to the case under limited communication. When the system has a variety of signal types in the networked control systems, it will be convenient to set the sampling periods and scheduling periods according to the feature of each signal. It will overcome the problem of the controllers in original discrete periodically varying systems constrained periodically by communication sequence. It will avoid periodically switching among multiple controllers, increase the design freedom of control system, and improve the system dynamical reconfiguration capability and overall performance.

Keywords:networked control system; communication constraints; linear matrix inequalities; Kalman filtering; LQG optimal control

通过共享网络形成的闭环反馈控制系统称为网络控制系统[1-3]，其中，传感器，控制器，执行器之间的信息传输是通过共享式数字网络进行信息交换的.网络的介入给控制系统带来诸多的优点，但同时也不可避免地给控制系统的设计和分析带来更多的挑战.有限的带宽，数据包的传输速率和长度以及介质访问控制协议等都会给网络控制系统的性能带来影响[4].因此，传统的设计方法已不再适用于网络控制系统，需要探索新的设计方法.针对通信受限带来的问题，现有的研究结果大致可分为以下几类：第一类方法的主要思想是将网络服务质量(Quality of serviece，QoS)对系统控制性能(Quality of performance，QoP)的影响抽象为具有不同特性的时延、丢包等因素，忽略网络的存在并按常规方法设计控制器[5-9].这类方法主要侧重于NCSs中控制系统稳定性的保证，但不利于提高系统的总体性能.第二类则是从QoS角度出发研究调度策略，即从通信技术的角度研究合适的信息传输方式或带宽配置策略等，确保事先设计好的控制算法的有效实施[10-11].这类方法将控制性能要求简单定义为保证数据传输的实时性及可靠性，因而不能完全了解控制系统的总体性能[12].

以上方法为降低控制系统设计的复杂性，往往忽略控制器和调度器设计的耦合性，因而对于保证系统的总体性能尚存不足.第三类方法通过对NCSs中的控制与通信问题进行综合考虑以解决这一问题，称为控制与调度的协同设计方法[13-15].现有系统一般采用统一采样频率.然而，实际应用中诸多被控对象往往存在多种信号类型(如电机控制里同时具有温度，转速，电流等快变或慢变信号)及控制系统对不同信号量存在不同的控制要求.因此针对通信受限的多输入、多输出网络控制系统，根据其不同信号的不同特点，通过采用信号量非均匀采样(Non-uniform sampled-data)[16-17]的方式将其建模为集成控制与调度为一体的离散周期性系统.进而，根据Kalman滤波器思想设计了基于输出值的最优状态估计器，并基于线性矩阵不等式方法给出了最优保性能控制器的设计方法.

1通信受限NCSs模型

考虑一类通信受限的多输入、多输出网络控制系统，其系统结构如图1所示.假设被控对象为具有m个输入和r个输出的离散线性时不变系统，可用状态方程描述为

(1)

其中：T为系统采样周期；x(kT)∈Rn，u(kT)∈Rm，y(kT)∈Rr分别为系统的状态向量、控制输入向量以及测量输出向量；A∈Rn×n，B∈Rn×m，C∈Rr×n分别为适当维数的系数矩阵；过程噪声ω(kT)，测量噪声v(kT)服从高斯独立同分布，且满足ω(kT)～N(0,G)，v(kT)～N(0,Ir×r)，其中Ir×r为r×r维单位矩阵，G为n×n维正定矩阵.同时假定系统初始状态x(0)满足x(0)～N(x0,P0).

图1　介质访问约束NCSs系统模型Fig.1　Diagram of NCSs with communication constraints

假设每个采样周期内，NCSs中仅有有限个节点能够通过网络传输数据.如图1中被控对象具有m个输入和r个输出，其中m个执行器共享输入通道，r个传感器共享输出通道，由于介质访问约束共享输入通道数通常小于m个，而共享输出通道数小于r个，即在每个采样周期T内，r个传感器共享bs(1≤bs

1.1通信受限特性描述

为了给出通信受限的NCSs模型，首先给出如下定义：

定义1定义二值函数σβ(t)∈{0,1}(j∈1,2,…,m)和δα(t)∈{0,1}(i∈1,2,…,r)分别代表t时刻系统执行器和传感器的工作状态.若σj(t)=1，则表示第β路控制输入uβ在t时刻被更新；否则，则表示uβ在t时刻不被更新.同理，若δα(t)=1，则表示第α路采样输出yα在t时刻能够通过网络传输至控制器；否则，则表示yα在t时刻不能传输至控制器.

根据定义2，3，此类通信受限NCSs的网络资源约束条件可以表示为

∀k1,k2,i∈[0,N1-1],j∈[0,N2-1],

(2)

举例说明，令δ(t)=[1,1,0,1]T时，则

举例说明，令σ(t)=[1,1,0,1]T时，则

1.2系统模型

采用提升技术[19]来推导系统模型，假设系统模型如式(1)所示，令N为更新序列周期N1和采样序列周期N2的最小公倍数，即

N=LCM(N1,N2)

同时，令T0=NT，则T0为帧周期，即整个系统的循环周期.

由式(1)可得，在不考虑噪声的情况下可得离散化模型，即

同理，递推可得

依此类推，可得

令系统的控制输入向量、测量输出向量的增广形式分别为

同理，分别令控制器输入向量和输出向量的增广形式分别为

(3)

(4)

其中：

(5)

其中：

Ar=AN，Br=[AN-1B…ABB]

2系统LQG控制器设计

最优LQG控制器的具体结构见图2.考虑被控对象的过程干扰和测量干扰，系统控制器的设计可分为两步：

图2　具有LQG控制器的NCSs结构图Fig.2　Diagram of NCSs with LQG controller

2.1状态估计器设计

假设滤波器的估计状态形式为

(6)

(7)

将式(7)两端取期望值，可得

(8)

定义状态估计误差的协方差为

(9)

根据式(7~9)可得

(10)

极小化这个协方差矩阵可得到最优的增益矩阵和协方差矩阵分别为

(11)

(12)

综上所述，由式(6，11，12)构成了系统的状态估计算法.

2.2最优状态反馈控制器

为求解控制器增益K，可以考虑式(5)所对应确定系统的LQG问题，即不考虑噪声干扰的情况.假设没有噪声干扰的系统状态空间模型为

(13)

设系统的状态反馈控制器为

(14)

同时，考虑控制器设计的性能指标为

(15)

其中：Q和R分别为已知的正定加权矩阵.

引理1[20]对于式(13，15)，存在对称正定矩阵P>0和矩阵K，使以下矩阵不等式成立时，即

(16)

定理1当且仅当存在矩阵Y和对称正定矩阵X>0，使得以下线性矩阵不等式成立时，即

(17)

证明由引理1可知：当式(16)成立时，式(13)存在一个保性能控制器.根据Schur补性质可知式(16)等价于

(18)

在式(18)的左右两端分别乘上矩阵diag{P-1,I,I,I}，并取X=P-1，Y=KP-1即可得到矩阵不等式(17).定理得证.

式(17)是关于变量X和Y的一个线性矩阵不等式，因此可以利用LMI工具箱中的求解器feasp来求解此线性矩阵不等式的可行性问题，并利用得到的可行解来构造所求的二次保性能控制律.

定理2对给定的式(13，15)，有

(19)

针对一个存在通信受限的多输入多输出被控对象设计输出反馈LQG控制器的主要步骤如下：

Step 1在满足约束条件的前提下，选择适当的采样序列和更新序列以保证系统的能控性和能观性不变.

Step 2根据式(5)确定系统增广状态空间模型的系统矩阵.

Step 4根据定理2，利用LMI工具箱中的求解器mincx求解线性矩阵不等式(19)，得到状态反馈控制器式(14)的增益矩阵K.

3仿真结果

考虑一个控制系统，其离散状态空间模型为

下面分别考虑在两种不同的调度策略下，系统控制性能指标的变化.

1) 根据约束条件选取以下更新序列和采样序列，即

其中更新序列周期Tu等于采样序列周期Ty，即N1=N2=2，则系统的帧周期T0=2T.

图4　状态估计误差曲线Fig.4　The error curves of the state estimation

图5　系统状态响应曲线Fig.5　The state response curves

2) 同理，根据约束条件选取以下更新序列和采样序列为

{[1,0]T,[1,0]T,[0,1]T}

{[1,0]T,[1,0]T,[0,1]T}

图6　状态估计误差曲线Fig.6　The error curves of the state estimation

图7　系统状态响应曲线Fig.7　The state response curves

从仿真结果可以看出：对于相同通信通道约束条件，选择不同的调度策略，可以得到不同的系统性能指标.因此，调度策略的选取同样能够影响系统的性能.

4结论

针对通信受限的多输入、多输出网络控制系统，研究了LQG控制器的设计问题，分析了由于网络受限给系统建模带来的影响.采用提升技术建立了通信受限NCSs的增广状态空间模型，此模型集成了调度信息，并同时保持了原被控对象的时不变性质，为控制器分析提供了方便.接着，根据输出值设计了基于Kalman滤波思想的状态估计器以提供状态估计最优值，利用LMI分析了系统保性能控制器的设计方法.该方法特别适用于被控对象存在不同类型控制信号的情况下，可方便地针对不同信号的特征设计相应的采样频率和通信序列，其控制设计的自由度和动态重构能力都能有效提高，而且更方便系统采样周期调度和工程化实施.

参考文献：

[1]王雅琳，凌翔，桂卫华，等.网络控制系统中通信信道受限对LQG最优控制性能影响[J].小型微型计算机系统，2009，30(4):661-665.

[2]何德峰，周洲，郭海锋.网络化控制系统鲁棒动态矩阵控制[J].浙江工业大学学报，2013，41(1):91-95.

[3]SAMIRA，VASILED.filteringofperiodicMarkovianjumpsystems:applicationtofilteringwithcommunicationconstraints[J].Automatica，2012，48(12):3151-3156.

[4]孙连坤.网络化控制系统调度与控制协同设计[D].天津：天津大学，2009.

[5]TATSUOS，MICHIOK，NOBUYAT，etal.Controllabilityandstabilizabilityofanetworkedcontrolsystemwithperiodiccommunicationconstraints[J].Systems&ControlLetters，2011，60(12):977-984.

[6]SONGHongbo，YULi，ZHANGWenan.Stabilisationofnetworkedcontrolsystemswithcommunicationconstraintsandmultipledistributedtransmissiondelays[J].IETControlTheoryandApplications，2009，3(10):1307-1316.

[7]XUYong，SUHongye，PANYajun，etal.Stabilityanalysisofnetworkedcontrolsystemswithround-robinschedulingandpacketdropouts[J].JournaloftheFranklinInstitute，2013，350(8):2013-2027.

[8]LIUK，EMILIAF，LAURENTIUH.StabilityandL2-gainanalysisofnetworkedcontrolsystemsunderround-robinscheduling:atime-delayapproach[J].Systems&ControlLetters，2012，61(5):666-675.

[9]赵旋，何德峰，周洲.网络控制系统多变量dmc算法的稳定性分析[J].浙江工业大学学报，2012，40(2):209-212.

[10]WALSHGC，YEH.Schedulingofnetworkedcontrolsystems[J].IEEEControlSystemsMagazine，2001，21(1):57-65.

[11]仇翔，滕游.离散时滞系统的网络化保成本控制[J].浙江工业大学学报，2014，42(4):400-404.

[12]LIZuxin，WANGWanliang，CHENGXinmin.Optimalbandwidthschedulingforresource-constrainednetworks[J].ActaAutomaticaSinica，2009，35(4):443-448.

[13]ZHAOMingyue，LIUHeping，LIZhijun，etal.Faulttolerantcontrolfornetworkedcontrolsystemswithaccessconstraints[J].ActaAutomaticaSinica，2012，38(7):1119-1126.

[14]ZHOUChuan，DUMingli，CHENQingwei.Co-designofdynamicschedulingandH-infinitycontrolfornetworkedcontrolsystems[J].AppliedMathematicsandComputation，2012，218(21):10767-10775.

[15]LUZibao，GUOGe.Communicationsandcontrolco-design:acombineddynamic-staticschedulingapproach[J].SCIENCECHINAInformationSciences，2012，55(11):2495-2507.

[16]WEIChen，LIQiu.Stabilizationofnetworkedcontrolsystemswithmultiratesampling[J].Automatica，2013，49(6):1528-1537.

[17]ALBERTOSP，SALTJ.Non-uniformsampled-datacontrolofMIMOsystems[J].AnnualReviewsinControl，2011，35(1):65-76.

[18]ZHANGL，DIMITRIOSHV.Communicationandcontrolco-designfornetworkedcontrolsystems[J].Automatica，42(6):953-958.

[19]BAMIEHB，PEARSONBJ，TANNENBAUMBAF.Aliftingtechniqueforlinearperiodicsystemswithapplicationstosampled-datacontrol[J].System&ControlLetters，1991，17(2):79-88.

[20]俞立．鲁棒控制：线性矩阵不等式处理方法[M]．北京：清华大学大学出版社，2002．

(责任编辑：刘岩)

作者简介：邵奇可(1977—)，男，浙江舟山人，副教授，博士，研究方向为网络控制系统，E-mail：sqk@zjut.edu.cn.

基金项目：国家自然科学基金资助项目(61104095)

收稿日期：2014-10-24