基于IC卡数据的地铁列车开行方案的精细化编制*

郑亚晶　靳文舟

(华南理工大学 土木与交通学院， 广东 广州 510640)

基于IC卡数据的地铁列车开行方案的精细化编制*

郑亚晶靳文舟†

(华南理工大学 土木与交通学院， 广东 广州 510640)

摘要：以IC卡刷卡数据为客流基础，探讨了基于IC卡数据的地铁列车开行方案精细化编制方法.在分析传统地铁OD客流统计方法存在的问题基础上，提出了一种新的地铁列车开行方案编制方法，充分讨论乘客乘坐地铁的过程，利用数据挖掘技术对IC卡刷卡的原始数据进行补全、拆分，从而实现了地铁列车开行方案的精细化编制.针对地铁IC卡刷卡数据的应用结果表明，文中提出的列车开行方案编制方法便于操作，和传统的地铁OD客流统计方法相比更能适应实际客流的需要.

关键词：地铁；IC卡数据；客流统计；开行方案

地铁列车开行方案是地铁运营组织工作的核心内容，也是编制地铁列车运行图的基础.一般来说，传统的地铁列车开行方案在形式上等同于交路上的分时段(一般以小时为单位)列车开行对数.因此，在某种意义上，传统的编制列车开行方案[1]的核心工作就是确定地铁的分时段断面客流量.不过，随着地铁越来越重视调度工作的精细化控制，传统的列车开行方案编制方法也越来越不适应我国地铁的发展实际.

传统的地铁分时段断面客流，以客流的统计OD为基础，一般通过调查问卷的方式获得数据，其准确性和可靠性都值得怀疑，由此得出的地铁列车开行方案的适用性也显然值得商榷.此外，传统方法中将客流量分时进行统计(以小时为间隔)的方法无法反映1 h内客流的变化情况，并且在根据分时段客流编制开行方案时，直接给各个分时段(单位时间)指定载客率的做法也显得较为随意.

为解决传统方法中的问题，不少学者对列车开行方案的编制进行了深入研究[2-6]，采用优化建模的方案对地铁列车开行方案进行探讨.这些方法虽然避免了传统方法上的相关问题，不过从实际运用的角度来说，都较为繁琐，一些参数(例如广义出行费用[4])的值在实际工作中也较难确定，这也使得相关的研究成果在地铁实际运营中的运用效果并不理想.

而随着IC卡在地铁中的广泛使用，其庞大的刷卡数据为获取客流数据提供了真实和准确的来源，而利用刷卡数据编制地铁列车开行方案的研究也引起了不少学者的关注[7-9]，但相对于公交刷卡数据的研究[10-14]来说，还不够充分和完善.具体地说，地铁的IC卡刷卡数据在属性上与公交IC卡刷卡数据有以下的几点区别：①地铁刷卡记录包含进站和出站信息，但有大部分公交车刷卡记录仅包含上车信息而不包含下车信息；②地铁刷卡记录所采集的是乘客进出站时间，而公交车刷卡记录所采集的是乘客上车时间；③地铁刷卡记录不采集换乘信息，而公交刷卡记录则采集换乘信息.

以上的不同使得众多学者基于公交刷卡数据的相关成果并不适用于地铁，故文中拟通过对地铁刷卡数据的挖掘，充分考虑地铁刷卡数据的特性，提出更符合实际情况、更易于实现且更加精细的地铁列车开行方案编制方法.

1地铁出行过程

乘客的地铁过程一般以起始站进站刷卡为起点，而以终到站出站刷卡为终点，起点和终点之间的过程为一次地铁出行，如图1所示.

图1　乘客地铁出行过程示意图Fig.1　Diagram of the passenger travel process

在乘客乘坐地铁出行的过程中，乘客仅在起始站进站和终到站出站时进行刷卡操作，在换乘时乘客并不刷卡，因此乘客换乘的路径并不能依靠刷卡记录确定.根据乘客的刷卡数据，以及我国地铁线路规划和换乘的一般情况，可作如下基本判断：①当乘客的起始站和终到站在同一地铁线路时，乘客的该次地铁出行不进行换乘；当进出站车站位于不同地铁线路时，乘客的该次地铁出行需要进行换乘；②地铁IC卡分为储值卡和单程票两种，单程票的刷卡数据(主要是出站刷卡数据)存在丢失现象[15]，而储值卡的刷卡数据一般不存在数据丢失；③乘客的一次地铁出行行为包含两次刷卡(起始站进站刷卡和终到站出站刷卡)过程.

对于地铁IC卡后台数据来说，虽然目前我国各个城市的地铁IC卡刷卡数据格式并不统一，但无论哪个城市的地铁刷卡数据都包含刷卡时刻、闸机编号、IC卡卡号、进出站标记等字段.因此要获得一条描述地铁一次出行的记录，按照前文所述的基本判断第3条，只需找到相对应的起始站进站刷卡记录和终到站出站刷卡数据即可：将同一卡号下的刷卡数据按刷卡时间升序排列，标记为进站的某条数据和标记为出站的下一条数据即为对应数据，如果进站数据对应的出站数据缺失，则用空白数据“补足”.至此，两条刷卡数据即可合并为一条地铁的出行记录(文中在计算机实现过程中为确保数据的准确性，还利用票价、进出站点、进出站时间等因素之间的关系对得到的一次地铁出行记录进行了判断)，这一过程的计算机实现如图2所示.

图2　地铁出行记录的计算机统计IC卡数据实现原理Fig.2　Principle of counting the IC card data on the travel records by computer

表1为将刷卡数据统计为出行记录后得到的地铁出行记录表(全文均以北京地铁为例)，其中序号为4的记录因为单程票的流失，出站数据被空白“补足”.

2数据的补全

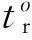
假设ZoY表示乘客由起始站站点o出发，花费费用Y到达的终到站站点集，Poj表示在即有统计数据中，由站点o至站点j的客流量，其中j∈ZoY.则终到站站名补全为站点i的概率Fi如下：

(1)

在地铁刷卡的后台数据中，由于缺失数据记录的主体是单程票，而从乘客属性来说，使用单程票的乘客和使用储值卡的乘客有很大不同(单程票使用者以外来短期居住人口为主，储值卡使用者以长驻人口为主).故在式(1)中，Poi及Poj采用单程票客流量会更加符合实际情况.

在补全了终到站站点的情况下，待补全记录的出站刷卡的时刻与进站刷卡时刻之间的时间间隔的取值也应服从某一概率分布.这一概率分布可由既有数据中与待补全记录具有相同进出站站点的记录的进出站刷卡时间间隔统计获得，即要补全的出站刷卡时刻为

(2)

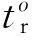
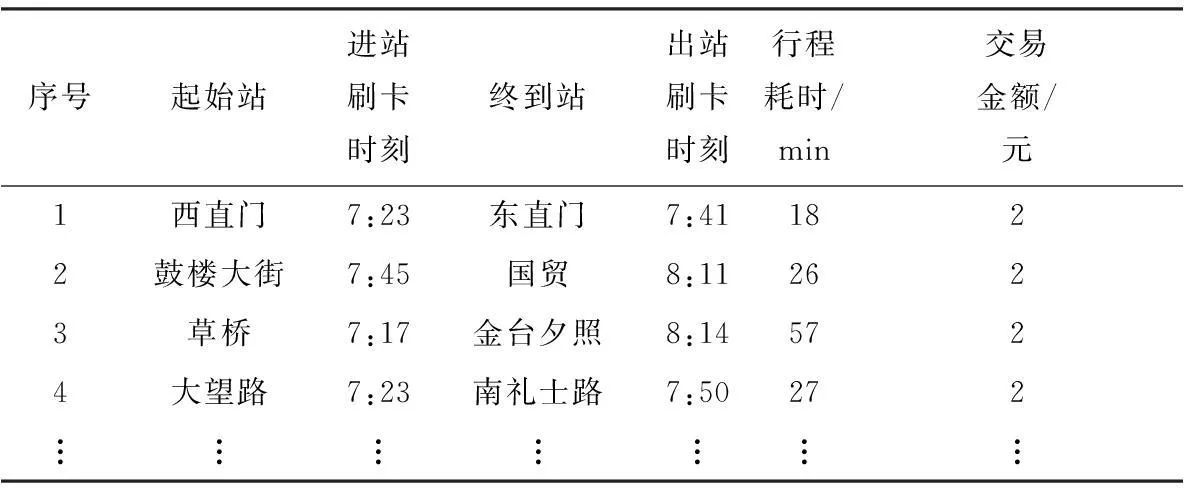
表2　补全后的地铁出行记录表Table 2　Completed travel records table of metro passengers

3乘客地铁全过程分析

图1所示的乘客地铁过程与实际的乘客过程有一些细微差异，即未涉及部分乘客因某些原因在站台短时逗留的情况.而通过对北京地铁和广州地铁的调研，部分乘客出现站台短时逗留一般基于以下3种原因：①部分乘客在线路首站会等待多趟列车，待有空座位后才会上车；②在高峰期，某些大客流站点的部分乘客需要等待多趟列车之后才能挤上列车；③乘客在起始站、换乘站或终到站的付费区等人.

而从调研数据的数量上来说，情况①和③出现的人数相对于情况②来说可以忽略不计，因此文中不对情况①和③予以讨论.而对于情况②来说，这显然是由于线路运输能力不够或者列车开行方案不适合客流所致.除此之外，以下的④、⑤两种情况也会增加乘客的地铁全过程时间：④离线路首站有两三站距离的部分乘客会先反向乘车到线路首站以便有座位；⑤乘客对线路不熟悉，坐错线路以至绕行过远或者乘客坐过了站.

不过对于这两种情况来说，无论是从人数上还是从影响效果上，都不会对最终的列车开行方案的编制造成太大影响.因此文中对这两种情况也不予考虑.

对于乘客的地铁过程来说，其在终到站的下车时刻(或者出站刷卡时刻)很显然受到列车开行方案的影响，因此对于客流统计来说，乘客在起始站站台的开始候车时刻，比终到站的下车时刻更加“自发”.换句话说，选用与开始候车时刻密切相关的进站刷卡时刻作为客流统计的基础数据比选用出站刷卡时刻更能真实地反映乘客的乘坐需求，且选用前者作为统计基础可以避免应上文所述原因②中客流需求和刷卡时刻之间的差异.

乘客在起始站的开始候车时刻和进站刷卡时刻之间的间隔即为乘客进站走行所花费的时间.对于同一个站台来说，乘客进站走行的时间长短与车站是否处于客流高峰期、乘客选择步梯还是电梯、乘客自身的属性等因素相关；而对于有多个站台的车站(例如换乘站)来说，乘客进站走行的时间长短还与具体的站台选择有关.根据在北京和广州的实地调研数据以及文献[16]中的标定参数，对地铁车站的乘客进站行为进行模拟仿真，结果表明，对于同一站台(除去西直门等走行距离特别长的特殊站点)，超过97%的乘客的站内走行时间差异在1min之内，也即乘客的个人属性差异以及个人步梯或自动扶梯的选择差异在文中时间精确到分钟的研究中可以予以忽略.从这点上来说，某乘客开始候车的时刻可由下式较为方便地求得：

(3)

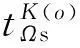
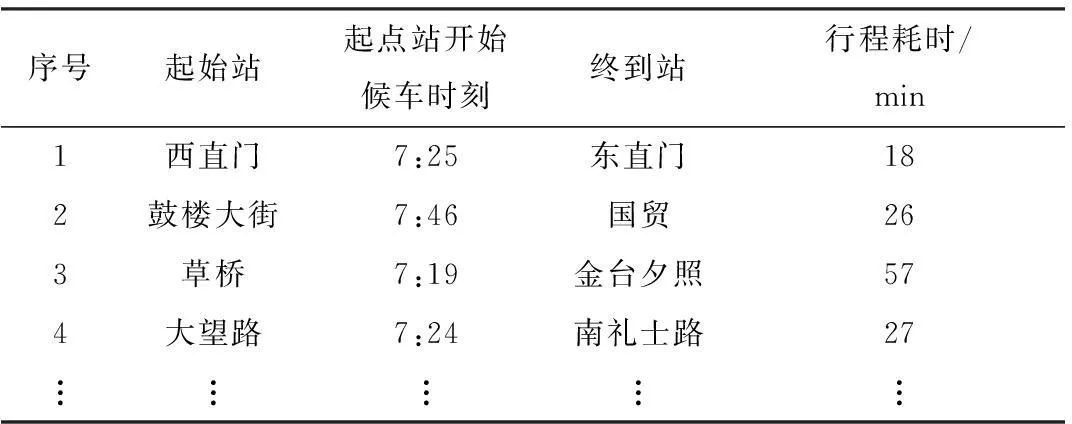
表3　转化后的地铁出行记录表Table 3　Converted travel records table of metro passengers

4数据的拆分

如果乘客起始站o所属的线路K与终到站i所属的线路L不是同一条线路，则说明该记录在地铁网络中进行了换乘；此外，对于环形线路，列车会在首末站进行改换车号作业.如果表3中的某条记录涉及到以上两种情况的任何一种，则需对该记录进行拆分，使得一条记录只涉及一条地铁线路的一个方向.

4.1　起始站和终到站不在一条地铁线路上的记录

对于起始站和终到站不在一条地铁线路上的记录，必须以换乘站为分割点将记录进行拆分.而显然，乘客对路径的选择决定着记录拆分的最后结果.一般来说，可以利用表3中的行程耗时时间来初步确定乘客的换乘路径.如果几条乘客可能的选择路径在时间上较为接近，行程耗时无法有效确定换乘路径时，则按换乘次数最小的原则进行确定，如果依然无法区分，则遵循总站数最小的原则进行确定.如果以上方法都无法确定乘客径路，则对可能的径路进行随机选择.例如表3中的记录2，就是以换乘站建国门为分界点，将该记录拆分为表4中的两条记录2-1和2-2.

4.2　环形线路上的记录

对于环形线路上的记录，应首先按环行线路的设置确定线路首末站(一般为同一个站).如果该记录不跨越环形线路的首末站，则该记录无需拆分，否则，需以首末站为分界点进行拆分，例如表3中的记录1，以北京2号线的首末站积水潭为分界点，将记录拆分为表4中的1-1和1-2.

而经过以上的拆分过程，表3即可转化为表4的形式，在表4中，每一行记录都只涉及一条线路的一个方向.

表4　拆分后的地铁出行记录表Table 4　Split travel records table of metro passengers

然后，再类似第3节中数据补全的过程补全表4因拆分数据导致的空缺(文中不再赘述)，此时，表4将补全为表5的形式.

表5　拆分并补全后的地铁出行记录表Table 5　Travel records table of metro passengers after splitting and completing records

5乘客期望列车的首站发车时间

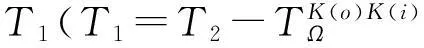
图3　乘客开始候车时刻和期望发车时刻之间的差异示意图Fig.3　Diagram of the difference between the time of the passenger start waiting for a train and the time of the passenger expecting the train pulling out of the first station

由此，可以将表5中的“起始站开始候车时刻”列转化为乘客的“期望首站发车时刻”列，再将该表按所属线路拆分并按“期望首站发车时刻”列升序排序，即可得到表6(仅以北京地铁2号线内环为例).

表6分线路和方向统计的地铁出行记录表

Table 6According to the line and direction statistics of metro travel records table

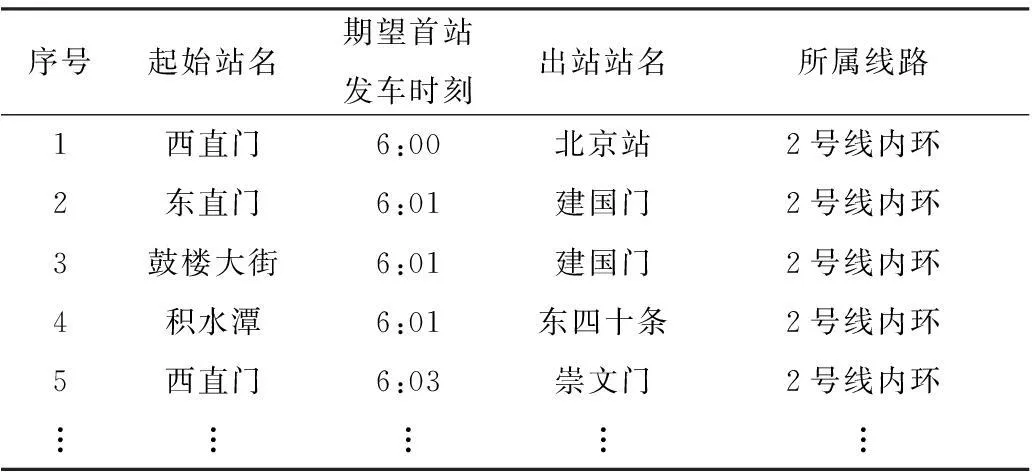
序号起始站名期望首站发车时刻出站站名所属线路1西直门6:00北京站2号线内环2东直门6:01建国门2号线内环3鼓楼大街6:01建国门2号线内环4积水潭6:01东四十条2号线内环5西直门6:03崇文门2号线内环︙︙︙︙︙

6列车开行方案的精细化编制

如果将列车开行方案的编制换一个角度定义，其实就是确定首发车的发车时刻以及之后各列列车和前一列列车的发车间隔.首发列车的发车时刻由运营的开始时间决定，因此编制列车开行方案的关键就是确定各列列车与前一列列车之间的时间间隔.

显然，发车间隔和列车满载率存在着一定的契合关系：发车间隔加大，可以提高列车的满载率；但同时发车间隔的加大又会导致乘客候车时间的增加.一般这一关系根据地铁线路的运营情况不同而不同.以北京地铁2号线内环为例，已知北京2号线内环使用的列车定员为1 428人，设定高峰期的服务水平为满载率100%(1 428人)，满载率最高不能超过120%(1 714人)，在非高峰期，为保证运输能力的利用率，应尽量使区间的最大满载率不低于40%(572人)；此外，若列车的最小发车间隔为2 min(由信号系统、折返设备等因素决定)，最大不能大于5 min(由提供给乘客的服务水平决定).为简单起见，可以将北京地铁2号线内环发车间隔和列车满载率的契合关系描述为：满载率100%对应发车时间间隔为2 min、满载率40%对应的发车时间间隔为5 min.文中将发车间隔和满载率定义为满足线性相关(发车间隔和满载率的契合关系的深入研究将另外撰文)，也即北京地铁2号线内环发车间隔和满载率之间的契合关系如图4所示(直线方程为：x+5y=7，x∈[2,5]).

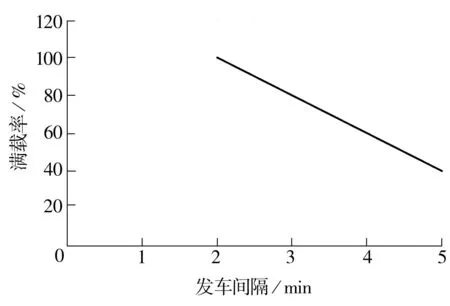
图4　发车间隔和满载率之间的契合关系Fig.4　Conjunction relationship between the interval and the full-load ratio

在某列列车(列车1)从首站开出后，在限制区间所累积的，期望乘坐下一列列车(列车2)的乘客，随着时间的推移将逐渐增加，将乘客数量转化为满载率，与发车间隔和满载率的契合关系线在同一坐标系中体现，则如图5所示.图中O′为起始点纵坐标，L1为列车承载能力上限，L2为发车间隔和满载率的契合关系线，S1、S2、S3、S4为不同情况下的乘客累积曲线(列车1发车后在限制区间有1 428×O′%位乘客在车站滞留).①当乘客的累积情况如S1线所示时，列车2应在列车1发出后2 min发车，且有部分乘客因列车容量原因无法上车，在站台滞留；②当乘客的累积情况如S2线所示时，列车2应在列车1发出后2 min发车，各站均无乘客因列车容量原因在车站滞留；③当乘客的累积情况如S3线所示时，列车2应在列车1发出后t′ min发车，各站均无乘客因列车容量原因在车站滞留；④当乘客的累积情况如S4线所示时，列车2应在内测1发出后5 min发车，各站均无乘客因列车容量原因在车站滞留.

图5　不同客流情况下的发车间隔策略分析Fig.5　Analysis of interval strategy under different passenger flows

由以上分析，只需统计线路上各区间的期望首站列车开行时刻的累积人数，即可实现地铁列车开行方案的精细化编制.根据这一思路，文中利用前文得到的表6数据，实现地铁列车运行方案的精细化编制.

表7　计算表格Table 7　The table is used to calculate

表7为精细化编制地铁列车开行方案的计算表格，其中T为该表格统计的表6中记录所对应的“期望首站发车时刻”，而表中第i列对应的ai为统计的客流量.按序号顺序将表6中的数据统计到表7，例如表6中的数据3，该数据起始站为鼓楼大街，终到站为建国门，因此该数据统计进表7后,表7中有变化的数据如下：

T为6:01，a2=a2+1，a3=a3+1,a4=a4+1，

a5=a5+1，a6=a6+1，a7=a7+1.

每当T有变化时，需进行是否发车检验，例如对于表6，在将序号为5的记录统计进表7之前，需对已统计记录进行列车2是否发车检验，此时T=6:02(取T将要变化时间的前1 min)，假设列车1从首站开出的时间为T0，则只需验算x=T-T0，y=max(a1,a2,a3,…)/1 428即可.①若x<2，不发车，继续统计；②若x=2，且y>120%，发车，列车2与列车1间隔2 min，表7中的ai按式(4)变化，开始下一趟列车的统计；③若x=2，且100%

(4)

当表6中的全部数据都执行完上述统计操作后，以上操作过程中确定的发车时刻即为文中所述方法编制出的精细化列车开行方案.

7结语

在文中的数据补全、记录拆分、确定列车始发站所需开出时刻以及最后的开行方案编制过程中，都需对数据进行遍历.为了提高程序的执行效率，可以将这4次遍历整合为一次，也即对每一条记录，都进行相应的处理并统计计入表7后，再跳到下一条数据.通过实际程序运行验证，在地铁实际数据非常庞大的情况下，这样整合处理能较好地节省编制开行方案的时间.

文中实现了基于IC卡刷卡数据的地铁列车开行方案精细化编制，并据此进行了相应的软件开发.该方法简单高效，从据此编制出的列车开行方案来看，列车数量与客流具有较好的贴合度，能够符合实际工作的需要.不过这一方法仅从客流的角度对列车开行计划的编制进行了探讨，并未对方案的可实施性进行研究(例如开行方案受到首末站折返线数量以及机车数量的限制等).此外，也未考虑地铁线路在高峰期采取的客流限制措施的影响，而满载率与发车间隔之间的契合关系，也有进一步深入研究的必要，这些内容将是下一步研究的重点.

参考文献：

[1]毛保华.城市轨道交通系统运营管理 [M].北京:人民交通出版社,2006.

[2]牛惠民,陈明明,张明辉.城市轨道交通列车开行方案的优化理论及方法 [J].中国铁道科学,2011,32(4):128-133.

Niu Hui-min,Chen Ming-ming,Zhang Ming-hui.Optimization theory and method of train operation scheme for urban rail transit [J].China Railway Science,2011,32(4):128-133.

[3]孟学雷,贾利民,卜萌,等.基于决策偏好可控的地铁列车开行方案设计研究 [J].铁道科学与工程学报,2012,9(1):46-50.

Meng Xue-lei,Jia Li-min,Bu Meng,et al.Train operation design based on decision preference controllable [J].Journal of Railway Science and Engineering,2012,9(1):46-50.

[4]邓连波,曾强,高伟,等.基于弹性需求的城市轨道交通列车开行方案研究 [J].铁道学报,2012,34(12):16-25.

Deng Lian-bo,Zeng Qiang,Gao Wei,et al.Research on train plan of urban rail transit with elastic demand [J].Journal of the China Railway Society,2012,34(12):16-25.

[5]孙焰,施其洲,赵源,等.城市轨道交通列车开行方案的确定 [J].同济大学学报:自然科学版,2004,32(8):1005-1014.

Sun Yan,Shi Qi-zhou,Zhao Yuan,et al.Method on ma-king train running-plan for urban railway traffic [J].Journal of Tongji University:Natural Science,2004,32(8):1005-1014.

[6]Odijk M A.A constraint generation algorithm for the construction of periodic railway timetables [J].Transportation Research,1996,30(6):455-464.

[7]周崇华.基于IC卡数据的深圳地铁OD信息处理技术 [J].城市轨道交通,2007(1):54-56.

Zhou Chong-hua.OD matrix of Shenzhen subway based on IC data [J].Urban Mass Transit,2007(1):54-56.

[8]周崇华.基于IC卡数据的地铁OD信息处理 [J].现代城市轨道交通,2007(1):47-49.

Zhou C hong-hua.IC data based OD information process in metro system [J].Modern Urban Transit,2007(1):47-49.

[9]邵星杰,黄长梅.南京地铁AFC系统断面客流的计算和应用 [J].通信与广播电视,2011(1):31-36;44.

Shao Xing-jie,Huang Chang-mei.Calculation and application of section passenger flow of Nanjing metro AFC system [J].Communication & Audio and Video,2011(1):31-36;44.

[10]师富民.基于IC卡数据的公交OD矩阵构造方法研究 [D].长春:吉林大学交通学院,2004.

[11]戴霄,陈学武,李文勇.公交IC卡信息处理的数据挖掘技术研究 [J].交通与计算机,2006,24(1):40-42.

Dai Xiao,Cheng Xue-wu,Li Wen-yong.Study of data mining technology on information process of bus IC card [J].Computer and Communications,2006,24(1):40-42.

[12]赵晖.基于公交IC卡信息的居民出行OD推算研究 [D].西安:长安大学信息工程学院,2009.

[13]章威,徐建闽.基于GPS与IC卡的公交OD量采集方法 [J].交通与计算机,2006,24(2):21-23.

Zhang Wei,Xu Jian-min.Public transit OD content acquisition method based on GPS and intelligent card [J].Computer and Communications,2006,24(2):21-23.

[14]胡郁葱,梁杰荣,梁枫明.基于IC卡数据挖掘获取公交OD矩阵的方法 [J].交通信息与安全,2012,30(4):66-70.

Hu Yu-cong,Liang Jie-rong,Liang Feng-ming.A way to get bus regional OD matrix based on mining IC card information [J].Journal of Transport Information and Safety,2012,30(4):66-70.

[15]程英俊.深圳地铁单程票流失算法研究 [J].都市快轨交通,2006,19(6):51-52.

Cheng Ying-jun.On the algorithm for the loss of single tickets in Shenzhen metro [J].Journal of Transport Information and Safety,2006,19(6):51-52.

[16]王子甲,陈峰,施仲衡.基于Agent的社会力模型实现及地铁通道行人仿真 [J].华南理工大学学报:自然科学版,2013,41(4):90-95.

Wang Zi-jia,Chen Feng,Shi Zhong-heng.Agent-based realization of social force model and simulation of pedestrians in subway passageway [J].Journal of South China University of Technology:Natural Science Edition,2013,41(4):90-95.

Elaborate Compilation of Running Plan of Subways Based on IC Card Data

ZhengYa-jingJinWen-zhou

(School of Civil Engineering and Transportation,South China University of Technology,Guangzhou 510640,Guangdong,China)

Abstract:Based on the passenger flow from IC card data,this paper discusses the way of compiling the running plan of subways based on IC card data.Then,by analyzing the problems of the traditional OD on the passenger flow of subways,a new method to compile the running plan of subways is proposed.In this new method,the process of the passengers riding the subways is taken full consideration and the data mining technology is used to complete and split the primary data of IC cards,and thus an elaborate compilation of running plan of subways is achieved.Finally,the proposed new method is used to handle the IC card data of subways.It is found that the proposed method is convenient to operate,and in comparison with the traditional methods,it is more adaptive for the needs of describing the actual passenger flow.

Key words:subways;IC card data;passenger flow statistics;running plan

中图分类号：U121

doi:10.3969/j.issn.1000-565X.2015.08.018

文章编号：1000-565X(2015)08-0119-07

作者简介：郑亚晶(1982-)，男，博士，讲师，主要从事城轨运营组织、调度优化研究.E-mail: ctyjzheng@scut.edu.cn†通信作者： 靳文舟(1960-)，男，教授，博士生导师，主要从事交通运营调度优化研究.E-mail: ctwzhjin@scut.edu.cn

*基金项目：国家自然科学基金资助项目(61473122)

收稿日期：2014-12-29

Foundation item: Supported by the National Natural Science Foundation of China(61473122)