嫦娥三号软着陆轨道设计与控制策略
岳 丽
(陕西国际商贸学院,陕西 西安 712046)
嫦娥三号软着陆轨道设计与控制策略
岳丽
(陕西国际商贸学院,陕西 西安 712046)
摘要:研究了嫦娥三号在进入着陆准备轨道后其相应位置、相应速度及各种姿态调整控制方向的确定问题,对嫦娥三号满足每个阶段关键状态的策略进行了优化,并实现了软着陆过程燃料消耗最少的控制。首先,利用椭圆运动的内部机理规律,结合椭圆的对称性建立初等模型,求得了着陆准备轨道近月点和远月点的位置和速度;其次,利用物体的重力势能和动能发生相互转换,以及机械能守恒和总机械能保持不变的知识建立了优化模型,运用函数作图得到并确立了嫦娥三号软着陆的最优轨迹方程;最后,依据误差分析法以及敏感性分析,建立了线性拟合模型,应用MATLAB软件,得到了嫦娥三号在相对情况下和绝对情况下的误差。其中,嫦娥三号软着陆中6个阶段的粗避障阶段对不确定因素最为敏感。得出了嫦娥三号着陆轨迹每个关键状态下路径坐标变化的位置,运用的算法简单明了,误差小,并且结果的检验和模型检验都具有相适应的精度和稳定性。
关键词:初等模型;优化模型;敏感性分析;线性拟合模型
嫦娥三号是中国国家航天局嫦娥工程第二阶段的登月探测器,它携带中国的第1艘月球车实现中国首次月面软着陆。软着陆作为踏上另一个星球进行实地科学探测的第1步,是所有探测活动中最为重要的环节。由于月球上没有大气,是真空状态,唯一的选择就是整个降落过程完全用着陆器底下的发动机朝反方向从下往上推,减少着陆器的下降速度。在整个“落月”过程中,嫦娥三号完全依靠自主导航控制,完成降低高度、确定着陆点、实施软着陆等一系列关键动作,人工干预的可能性几乎为零[1]。
1着陆准备轨道近月点与远月点的位置和方位的确定
1.1确定着陆准备轨道近月点与远月点位置的模型建立与求解
嫦娥三号着陆准备轨道为近月点15km、远月点100km的椭圆形轨道,将环月轨道(见图1)与月球近似为圆形,建立坐标系XOY,以X轴与Y轴的交点为环月轨道和月球的圆心点O。图1中,点A为近月点,点O为月球圆心与环月轨道圆心,点B为椭圆的圆心,点C为远月点,点D为着陆点。

图1 嫦娥三号环月轨道模拟图
以月球圆心为环月轨道的圆心,建立数学推导模型,利用比例分析法列出环月圆心轨道方程:X2+Y2=(100+R)2,其中R=1 737.013 km,得到点C(0,-1 837.013)、点A(0,1 752.013)、点B(0,-42.5)。已知点D(-356,91),得到tanα=4.665 8,tanβ=5.415 8,即α=77.90°,β=79.54°。嫦娥三号环月轨道方向是自西向东运动,以点E为参考点(见图2),其纬度是44.12°N,在月球的北半球。所以得出结论:近月点A的位置在着陆点D的北偏东12.1°;远月点B的位置在着陆点D的南偏东10.46°。

图2 E点方位图
1.2嫦娥三号在近月点、远月点相应速度模型的建立与求解
已知嫦娥三号是沿椭圆轨道运行,利用机理分析找出反映月球对嫦娥三号椭圆运动万有引力内部机理的规律,并建立数学模型。为使问题简化,可认为嫦娥三号以一个恰当的速率绕月心做匀速圆周运动,根据万有引力定律,月球提供其做圆周运动所需的向心力,由此可以得到嫦娥三号在近月点与远月点的万有引力恒等式[2]。
近月点:
远月点:
式中,R=1 737.013km;G=6.67×10-17N·km2/kg2,M=7.347 7×1022kg;h1=15km;h2=100km;得到近月点和远月点的速度分别为v1=52.89km/h,v2=51.65km/h。
1.3嫦娥三号在近月点与远月点方向的模型建立与求解
根据万有引力定律,月球对嫦娥三号提供向心力。根据推动机对其提供向上的推力,以及其自身受到的重力,从而分析出嫦娥三号在近月点的受力情况如图3所示。嫦娥三号在远月点受到的自身重力、牵引力、向心力以及自身的推力如图4所示。结合受力分析以及软着陆点的位置,可知嫦娥三号是逆时针运转。

图3 近月点的受力分析图 图4 远月点的受力分析图
2嫦娥三号软着陆运动轨迹模型
2.1嫦娥三号软着陆运动轨迹模型的建立与求解
根据机械能守恒定律,物体的重力势能和动能发生相互转换,其总机械能保持不变。在软着陆过程中,只有重力和发动机推力做功;因此,将两者的合力F合近似看作物体仅受的外力,抽象利用机械能守恒定律建立函数关系[3]。
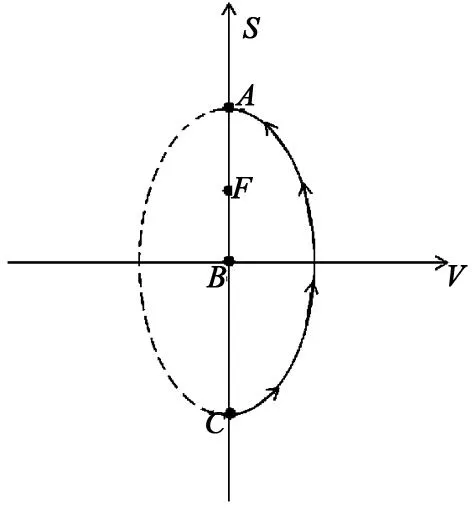
图5 椭圆轨迹坐标图
着陆准备轨道的近月点是15km,远月点是100km。近月点在月心坐标系的位置和软着陆轨道的形态共同决定了着陆点的位置。画出椭圆轨迹坐标图,以近月点和远月点之间的直线为v轴,以其垂直平分线为s轴,建立直角坐标系(见图5)。
设椭圆方程为:
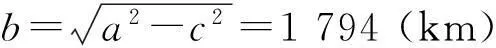
2.2主减速轨迹的模型建立与求解
主减速段的区间距离月面3~15 km。该阶段主要是减速,实现嫦娥三号距离月面3 km时速度降到57 m/s。嫦娥三号在主减速过程中受到自身的重力和推力,根据机械能守恒定律,建立主减速轨迹的优化模型如下:
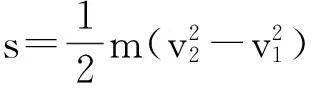
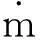
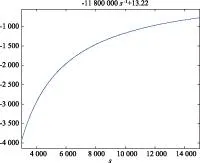
图6 主减速轨迹路径坐标变化图
2.3快速调整的轨迹模型建立与求解
快速调整段主要是调整探测器的姿态,需要在距离月面2.4~3 km处将水平速度减为0,即使主减速发动机的推力竖直向下。由动能守恒定律可知:
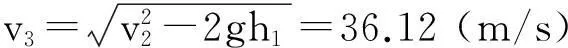
由:
可得:
建立探测器姿态快速调整的轨迹模型(见图7)。
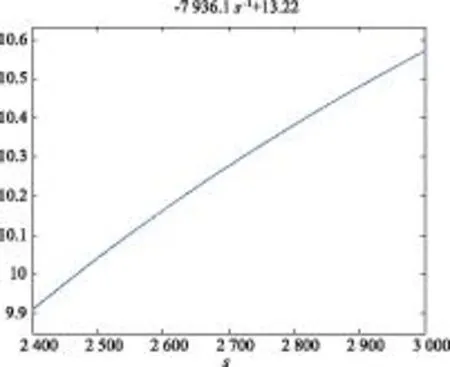
图7 姿态快速调整路径坐标变化图
2.4缓速下降轨迹的模型建立与求解
缓速下降阶段到开始4 m自由落体阶段的区间中是距离月面4~30 m。该阶段的主要任务是控制着陆器在距离月面4 m处的速度为0,从最后一个阶段倒推,算回到粗避障阶段。根据嫦娥三号在缓速下降中的受力分析,可知它受到重力、推力和阻力的作用,该阶段的主要任务是控制着陆器在距离月面4 m处的速度为0,即实现在距离月面4 m处相对月面静止,之后关闭发动机,使嫦娥三号自由落体到精确有落月点。在此期间,假设大推力主减速发动机的最大推动力为7 500 N。由F合=F推+G,可得a=1.93 m/s2。嫦娥三号推力向下做负功,即:
式中,v4是距离月面30 m处的速度;v5是距离月面4 m处的速度。
由于v5=0,得v4=10.01m/s;由:


图8 缓速下降的轨迹坐标化
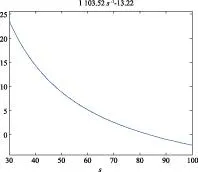
图9 精避障轨迹坐标变化图

图10 粗避障轨迹坐标变化图
3着陆轨道和控制策略误差分析和敏感性分析
3.1着陆轨道和控制策略做相应的误差分析
误差分析是指在完成系统功能时,对所要求的目标产生偏离的原因,后果及发生在系统的哪一个阶段进行分析,以消除或把误差减小到最低限度。嫦娥三号从椭圆轨道到着陆点的行径过程中,可以通过每个阶段中s的取值范围来确定误差。
各阶段s所取的中间值见表1,控制策略误差见表2。

表1 各阶段s所取的中间值

表2 各阶段控制策略误差
根据着陆轨道和控制策略做出相应的误差分析,控制策略模型使得嫦娥三号在快速调整阶段误差最大,精避障阶段误差最小。
3.2着陆轨道和控制策略做相应的敏感性分析
敏感性分析是指对确定嫦娥三号着陆轨道具有最大的潜在印象,并把其他所有不确定因素保持在基准值的条件下,考察每项要素的不确定性对目标产生影响的大小。
为了简化问题,本文假设向心力不对嫦娥三号做功;但由于敏感性分析,须重新考虑月球对嫦娥三号的向心力做功的影响,嫦娥三号受到向心力是从进入软着陆的主减速过程时开始,直到缓速下降阶段结束。根据机械能守恒定律,建立主减速轨迹的优化模型如下[5]:
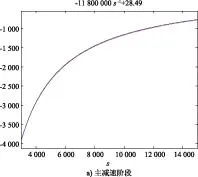

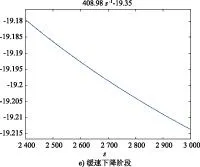
图11 各阶段运行轨迹图
通过分析比较,嫦娥三号的不确定因素——向心力,使整个软着陆过程中的粗避障阶段对其最为敏感。
4结语
利用机械能守恒定律,针对嫦娥三号进入环月轨道后6个阶段的轨迹方程建立了函数关系。并应用MATLAB软件,运用误差分析和敏感性分析对着陆轨道模型和控制策略的设计模型进行拟合,证实该模型可以得到较稳定的相适应性。然而在建立模型的过程中,欠缺计算机对数据和图像的运用及处理,导致存在一定的片面性,因此依旧需要就此展开讨论,深入研究。
参考文献
[1] 胡晓东,董辰辉.MATLAB从入门到精通[M].北京:人民邮电出版社,2012.
[2] 张洪华,梁俊.嫦娥三号自主避障软着陆控制技术[J].中国科学,2014,44(6):559-568.
[3] 蒋瑞,韩兵. 嫦娥三号着陆控制研究与软件仿真[J].研究与设计,2012,28(2):17-20.
[4] 张德丰,MATLAB自动控制系统设计[M].北京:机械工业出版社,2010.
[5] 姜启源.数学模型[M].北京:高等教育出版社,1993.
责任编辑郑练
Chang’e 3 Soft Landing Orbit Design and Control Strategy
YUE Li
(Shaanxi Institute of International Trade, Xi’an 712046, China)
Abstract:Study Chang’e 3 corresponding position, corresponding speed and the direction of the adjustment of all sorts of attitude control problem determination after entering orbit around the landing, let Chang’e 3 meet the state of each stage in the key strategy optimization, and achieve a soft landing process fuel consumption with the least control. First of all, utilize the internal mechanism of the elliptic motion regularity combining with the symmetry of the elliptical elementary model, we obtain the landing to track the location of the point and far point in recent months and speed. Secondly, by using the object’s gravitational potential energy and kinetic energy transformation, and the knowledge of the conservation of mechanical energy, the total mechanical energy remaining constant optimization model is established. The function and drawing methods are used to get the optimal landing trajectory is established. Finally, on the basis of error and sensitivity analysis of linear fitting model is established, use MATLAB software to obtain the Chang’e 3 error of the cases under the condition of relative and absolute position. Six stages of the Chang’e 3 soft landing stage of coarse obstacle avoidance of uncertainty factors are the most sensitive. It is concluded that the moon landing trajectory path coordinates in each key state change of position is presented, the algorithm is simple and clear with small error, and the results of test are appropriate to the precision and stability.
Key words:elementary model, the optimization model, sensitivity analysis, linear fitting model
收稿日期:2015-01-29
作者简介:岳丽(1982-),女,硕士,讲师,主要从事计算机辅助几何设计等方面的研究。
中图分类号:V 476.3
文献标志码:A

