电液舵机系统的建模及模型验证研究

王 博，陈万强，李祥阳

(西安航空学院， 西安 710089)

电液舵机系统的建模及模型验证研究

王 博，陈万强，李祥阳

(西安航空学院， 西安 710089)

电液伺服舵机系统是一套典型的非线性、参数不确定、有负载干扰的复杂系统，在建模的过程中，不但要考虑非线性的存在和负载不同模型的差异性，更要考虑到对模型简化的可行性，故理论建立的数学模型往往和实际差异较大，单纯依靠理论建模仿真并不能给工程人员提供可信的参考依据。为了验证模型的正确性，研究了电液舵机系统的理论建模过程，并对建立的模型进行验证实验，确定建立的数学模型。通过对比阶跃及扫频曲线的方法，对模型的动态、静态、频响特性进行对比分析，从而确定模型建立的正确性。对理论建模进行实验验证是必要的，不但可以指导理论建模，还可以为控制算法的计算机仿真带来有力的支持，并进而为电液舵机系统仿真平台的搭建提供基础。

舵机系统；Matlab；建模；电液伺服阀

舵机是飞行控制系统中的执行机构，其核心是一套电液伺服系统。该系统是按照放大器传来的控制信号,以一定的输出速度和输出力推动飞机的舵面，从而控制飞机飞行姿态的一套复杂装置。现代飞行器对性能的要求越来越高，操纵特性及气动力特性变得更为复杂，同时也对舵机的研制提出了更高的要求。然而，电液伺服舵机系统是一套典型的非线性、参数不确定、有负载干扰的复杂系统，在建模的过程中不但要考虑非线性的存在和负载不同导致的模型差异性，更要考虑对模型简化的可行性[1-8]。因为在对系统的分析和校正的过程中，如果模型不准确，将直接影响分析和校正的结果。要想得到一个高性能的电液舵机系统，验证模型的正确性很重要。通过物理仿真得到阶跃与扫频输出曲线，进而可得到相应的特性参数，与仿真曲线得到的特性参数相比较，就可以确定模型正确与否[2,9-13]。对理论建模进行实验验证是必要的，这不但可以指导理论建模，还可以为控制算法的计算机仿真带来有力的支持，进而为电液舵机系统仿真平台的搭建提供基础。

1 舵机系统原理

在电传操纵模态下，舵机通过位移传感器把作动器活塞的位移作为反馈信号，以此来控制电液伺服阀的运动。在该操纵模式下，舵机采用电液伺服阀控制作动器，再由作动器的输出力来推动舵面转动。系统构成一个闭合回路，是一个典型的电液伺服系统，其实质是通过电信号控制伺服阀把液压源的液压功率转换为作动器的机械功率输出。

2 舵机系统数学模型

2.1 电液伺服阀数学模型

从实用角度出发，一般可将复杂的电液伺服阀传递函数简化为二阶振荡环节[20]。因此，将本系统中的电液伺服阀传递函数描述为

(1)

其中：xv(s)为电液伺服阀的阀芯位移的拉氏变换；i(s)为电液伺服阀输入电流变化的拉氏变换；ωsv为电液伺服阀的固有频率；ζsv为电液伺服阀的阻尼比；Ksv为电液伺服阀的流量增益。

2.2 阀控缸环节数学模型

阀控缸环节数学模型见图1。

图1 阀控缸环节数学模型

1) 液压放大原件方程：

(2)

2) 作动器流量方程：

(3)

3) 液压缸的负载力平衡方程：

(4)

将式(2)～(4)合并同类项表示为

(5)

阀控缸环节完整的方块图如图2所示。

图2 阀控缸环节完整的方块图

当负载力只有惯性力时，系统相当于空载。由前述可知：滑阀输出流量方程和作动器输出流量相同，负载力平衡方程变为

(6)

式中：mt为负载和活塞折算到活塞上的总质量；Bt为作动器负载的阻尼系数；K为作动器负载的弹性系数。

对式(6)进行拉氏变换得

pfAt=mtxts2

(7)

同理，可得阀控缸环节空载方块图，如图3所示。

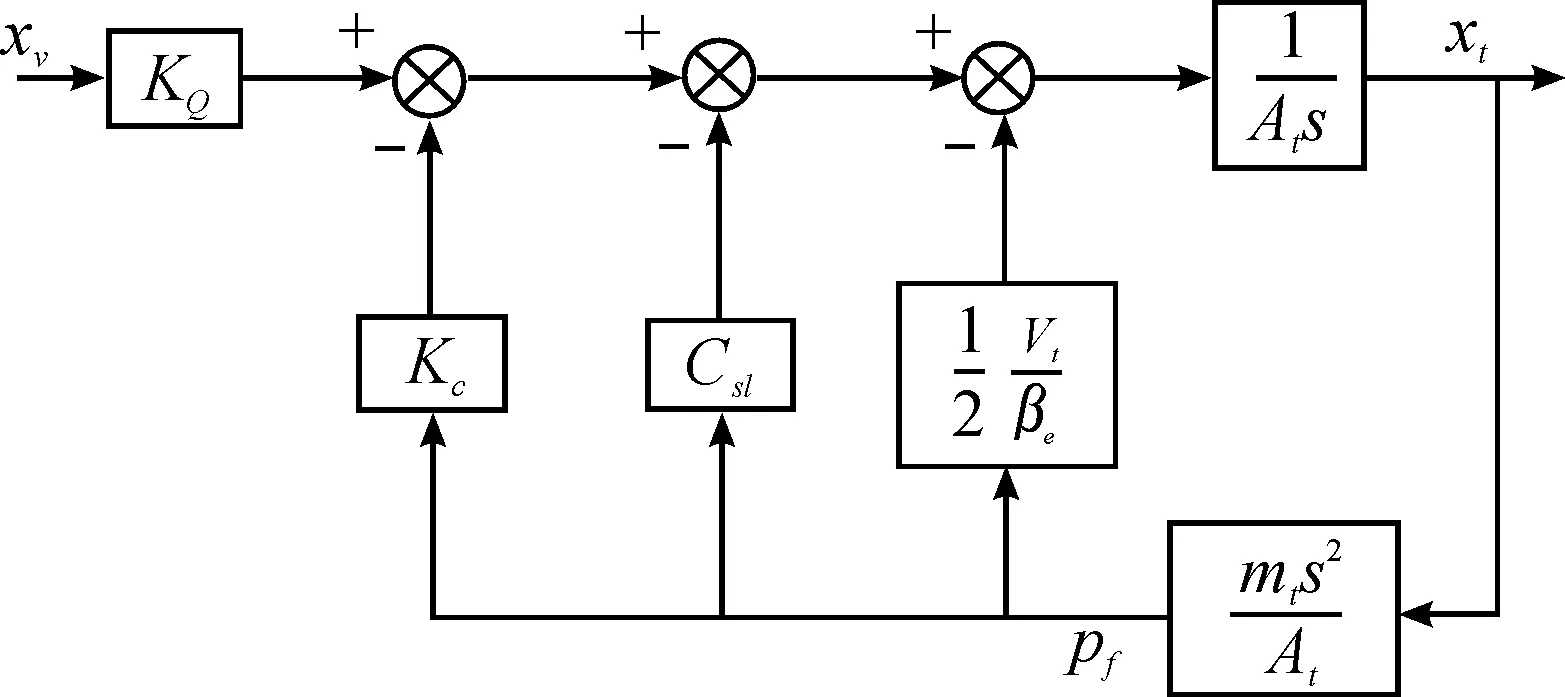
图3 阀控缸环节空载方块图

3 仿真研究

根据系统的理化特性建立系统的数学模型，仅考虑有弹性负载的情况。在此基础上，依据设计要求确定仿真参数，如表1所示。

通过仿真得到电传模式下的系统带宽为6.5 Hz。 令输入信号的频率为6.5 Hz，得到系统的输入/输出位移曲线，如图4所示。

从图4可以看出：输入信号的峰峰值为20 mm,输出信号的峰峰值为14.2 mm。此时的输出相角滞后为45.1°。

时域分析：设定δ1=0.014 mm，在系统输入5 mm 的阶跃指令，得到如图5所示的比例控制下舵机的阶跃响应曲线。

表1 系统仿真参数

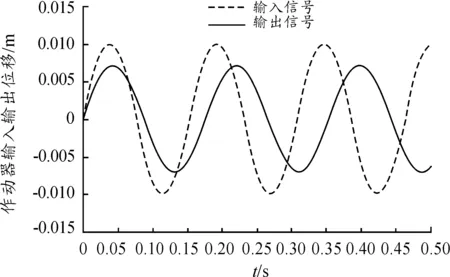
图4 系统的输入/输出位移曲线

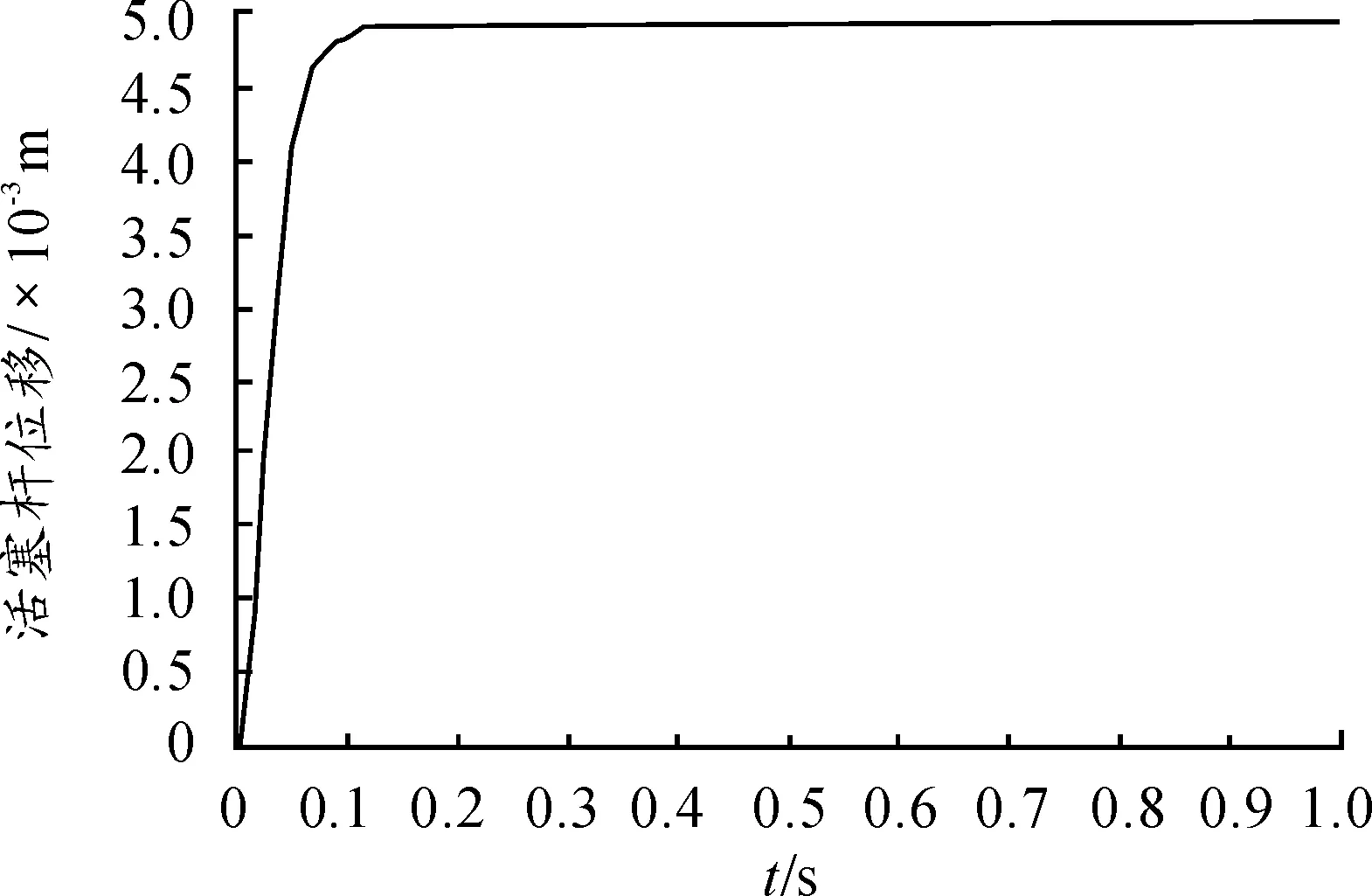
图5 比例控制下舵机的阶跃响应曲线

从图5可以清楚看出：虽然有死区存在，但给出的指令大小已远远超过死区的大小，所以在很短的时间内就可越过死区产生输出位移，即在0时刻就会产生位移。从图中还可以看到：系统有一个0.083 mm的稳态误差，该稳态误差即由死区产生。数据上升时间为0.049 8 s、调节时间为0.092 3 s，超调量为0。

4 物理实验对比

实验系统由实验台架、舵机实物、舵机控制器、测试系统、加载系统和能源系统组成。系统的组成示意图如图6所示。控制系统采用舵机专用控制器，其内部自带比例控制，为了与仿真作对比，比例系数仍取0.03，信号发生器为该控制器提供实验所需的电气指令信号。测试系统包括1台数据存储分析系统和1台外置16通道信号调理器及不同功能的传感器。实验只涉及线位移传感器。

图6 电传操纵模态实验系统组成示意图

数据存储分析系统选用奥地利DEWETRON公司的DEWE-2601，它是一台高性能的便携式数据采集分析系统。DEWETRON公司生产的专业测控处理机加上信号调理模块可以与各种传感器直接连接，实现从传感器到数据采集系统的方便连接，使电缆长度大为减少。所有程控模块的检测均由测试软件(DEWESOFT)自动完成，只需输入传感器的灵敏度和测试量程就可进行测试。测试软件界面如图7所示。

测试前检查油箱的油量、各个控制阀的状态是否为实验状态、管道是否有渗油漏油，确保各部分功能系统正常工作、板卡跳线设置正确等。对电传操纵舵机动态性能的测试主要有阶跃响应测试、频率响应测试。

图7 DEWESoft自定义测试界面

使用函数信号发生器对控制器发出5 mm阶跃控制指令，记录作动器活塞的位移曲线，如图8所示。

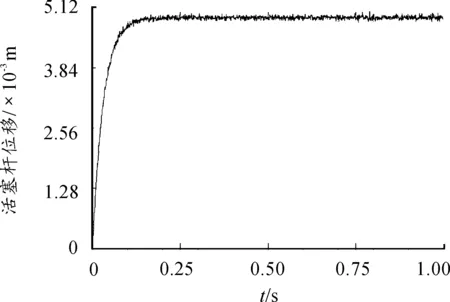
图8 实验记录系统阶跃响应曲线

从实验结果可以看出：上升时间为0.048 6 s、调节时间为0.095 1 s，稳态误差为0.061 4 mm，没有超调量。实验结果与仿真结果基本吻合。

当系统带宽为6.5 Hz时，为了与仿真进行对比，使用与仿真相同的输入参数，即峰峰值为20 mm，频率为6.5 Hz的正弦信号。使用函数信号发生器对系统发出扫频信号，记录作动器活塞的位移。实验结果如图9所示。

图9 实验记录系统扫频信号

从图9可以看出：输入信号的峰峰值为20 mm,输出信号的峰峰值为14.1 mm,输出位移/输入位移=0.705<0.707,表明结果基本符合要求。此时，在图上读出输出位移的相角滞后为45.8°，与仿真结果相符。

5 结束语

实验数据和仿真数据基本一致，验证了系统模型的建立方法是正确的。该模型可作为后续工作的仿真平台基础，在此基础上可进行其他校正环节的研究。如此，不但可大大提高工作效率，更主要的是解决了仿真结果与实际结果的偏差问题，通过仿真就可基本确定参数的大致范围，为最终调试提供依据，减轻了现场调试的盲目感。

[1] 吴晓男,陈勇,戴洪德.液压舵机模型仿真设计与研究[J].仪表技术,2013(6):45-48.

[2] 黄忠霖.控制系统MATLAB计算机及仿真[M].北京:国防工业出版社，2001:201-204.

[3] 刘国平,齐大伟,胡瑢华,等.比例方向阀性能测试系统设计[J].现代制造工程,2013(1):28-30,41.

[4] 王鸿钰.压缩机性能测试系统[J].电子质量,2002(3):18-21.

[5] 马丽,张秀彬,赵丽欣.基于虚拟仪器的机载模块性能测试系统[J].航空电子技术,2013(4):18-23.

[6] 崔胜民,李建如.基于虚拟仪器的汽车制动性能测试系统[J].汽车科技,2004(5):36-37.

[7] 成可南.计算机系统在自动化仪器仪表中的应用[J].自动化与仪器仪表,2014(7)：30-33.

[8] 徐波.自动化仪器仪表行业的现状及发展趋势[J].科技创新与应用,2014(13):31-34.

[9] 李洪人.液压控制系统[M].北京：国防工业出版社，1981:96-120.

[10]李培滋,王占林.飞机液压传动与伺服控制(下)[M].北京:国防工业出版社,1980:1-10.

[11]李艳军.飞机液压传动与控制[M].北京：科学出版社,2009:46-47.

[12]李玉琳.液压组件与系统设计[M].北京:北京航空航天大学出版社,1991:30-40.

[13]梅里特H E著.液压控制系统[M].陈燕庆,译.北京:科学出版社,1976:11-20.

[14]李叶妮, 林少芬,陈水宣.基于LabVIEW的液压伺服测控系统开发[J].重庆理工大学学报(自然科学版)，2012(8)：31-35.

[15]范子荣,滕青芳 . 液压伺服控制系统的设计[J]. 计算机仿真,2014(7):183-186.

[16]肖前进，贾宏光，章家保，等. 电动舵机伺服系统非线性辨识及补偿[J].光学精密工程,2013(8):2038-2047.

[17]崔业兵,鞠玉涛,周长省,等. 一种高带宽四舵翼电动舵机的可行性研究[J].电机与控制学报,2012(12):87-93.

[18]韩松杉,焦宗夏,尚耀星,等.基于舵机指令前馈的电液负载模拟器同步控制[J].北京航空航天大学学报,2015(1):124-132.

(责任编辑 杨黎丽)

Modeling and Electro-Hydraulic Steering System Model Validation Studies

WANG Bo，CHEN Wan-qiang，LI Xiang-yang

(Xi’an Aeronautical University, Xi’an 710089, China)

Electro-hydraulic servo steering system is system that has a typical nonlinear, parameter uncertainty and has a complex system load disturbance. In the modeling process, we not only have to consider the difference between existence and non-linear loads of different models, but also has to take the feasibility of the simplified model into account, thus there are often great differences between the mathematical model established based on theory and the actual situation, because relying on theoretical modeling simulation can not provide reliable reference for engineering personnel. In order to verify the accuracy of the modeling, theory model process of electro-hydraulic servo system was researched, and the model was verified to determine the established mathematical model. By comparing the step and sweep frequency curve method, the dynamic, static, and frequency response characteristics of model were analyzed to determine the accuracy of the establishment of the model. The theoretical modeling test is necessary, which can not only guide theory modeling, but also bring strong support for the control algorithm of computer simulation, and provide the basis for the construction of the electrohydraulic servo system simulation platform.

actuator system; Matlab; modeling; electro-hydraulic servo valve

2015-07-10 基金项目：2013年西安市科技计划项目(CXY1349(5));陕西省自然科学基础研究计划项目(2014JM2-5069)

王博(1984—),男,陕西人,硕士研究生,主要从事液压伺服控制研究。

王博，陈万强，李祥阳.电液舵机系统的建模及模型验证研究[J].重庆理工大学学报(自然科学版)，2015(12):133-137.

format：WANG Bo，CHEN Wan-qiang，LI Xiang-yang.Modeling and Electro-Hydraulic Steering System Model Validation Studies[J].Journal of Chongqing University of Technology(Natural Science)，2015(12):133-137.

10.3969/j.issn.1674-8425(z).2015.12.022

TM571.6+4

A

1674-8425(2015)12-0133-05