Stein岭型主成分估计下的单个数据删除模型的研究

朱 宁，严冠东

(桂林电子科技大学 数学与计算科学学院，广西 桂林 541004)

0 引言

考虑一般线性模型：

1 主要结果

2 诊断统计量

2.1 PRESS统计量

Allen（1971）[6]提出 PRESS 统计量，用来度量模型拟合的好坏。

定义1：在Stein岭型主成分估计下，把 PRESS=

2.2 协方差比统计量

2.3 AP统计量

AP统计量是由Andrew,D.F.和Pregibon,D.[9]提出的，在协方差比的基础上进一步考虑(yi，xi′)对 σ^2的影响。Drape和John[9]对AP统计量进行分解，提出探测强影响点的统计量新形式。

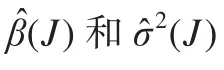
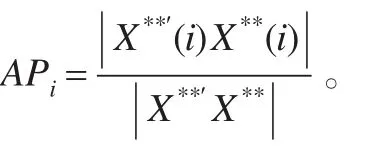
2.4 Cook统计量

Cook统计量是Cook（1977）[10]提出Cook统计量作为度量第i个数据点 (yi，xi′)影响大小的数量指标。

引理4：广义Cook统计量为

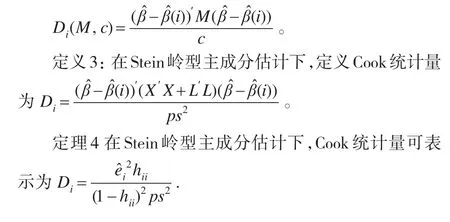
3 案例分析

本案例的数据来自文献[1]，这组数据存在较为严重的共线性，为了避免其共线性对估计量带来较大误差，我们在这定义Stein岭型主成分估计是必要的。我们主要考虑数据删除模型的拟合好坏程度。如果线性模型拟合较好，则去掉一、二个数据点后得到相应数据删除模型参数的估计量应该不会有显著的影响；如果有显著的影响，则说明数据集中有异常点或强影响点。计算影响度量统计量结果如下表：

从上表结果，我可以看出：

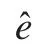
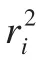
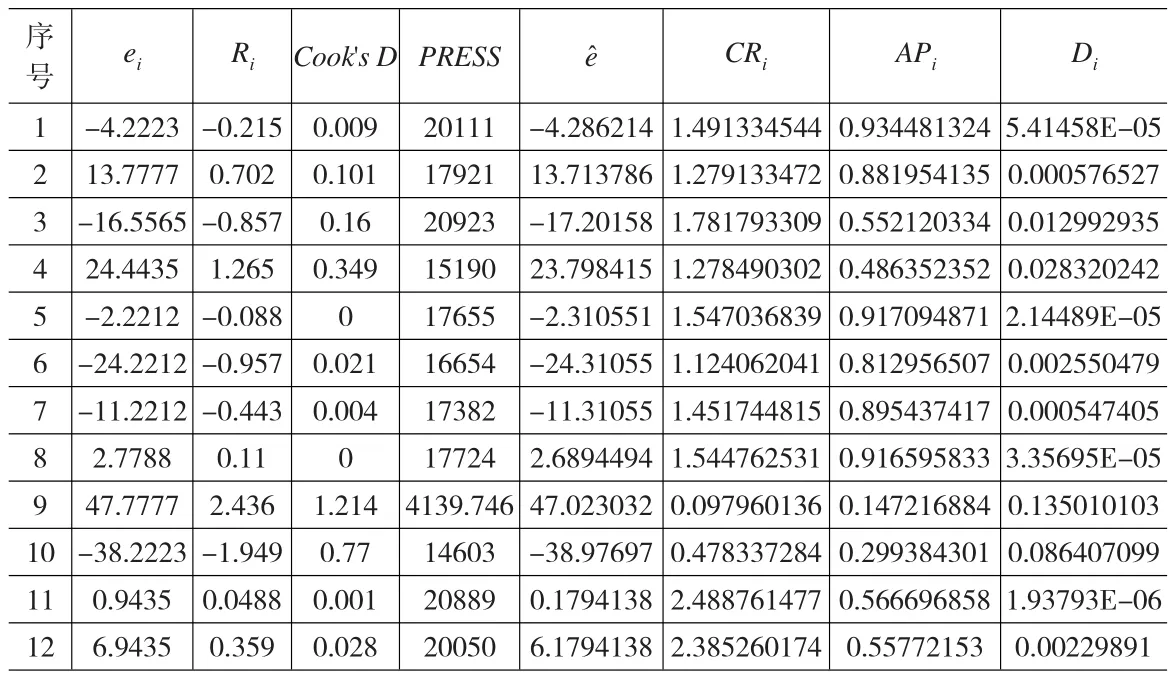
表1 净化煤数据

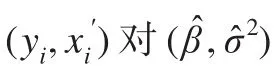
4 总结

Stein岭型主成分估计下数据删除模型与最小二乘估计下线性模型的估计量存在关系，可以通过表达式互相表示。

通过上面的讨论，得出结论：第九号数据是强影响点，由表中的度量数据的影响方面总体效果具有一致性，都可以用来分析强影响点，因此这四个统计量对诊断数据是否为强影响点是具有统计意义的。

[1]韦博成.统计诊断引论[M].南京:东南大学出版社,1991.

[2]林路.数据删除模型和均值漂移模型对岭估计的影响[J].邵阳师专学报，1994，（2）.

[3]钱峰，石丽娟.数据删除模型对于广义岭估计的影响[J].南通大学学报，2008，7（1）.

[4]朱宁，黄黎平.岭型主成分估计下数据删除模型的强影响分析[J].统计与决策，2012，(15).

[5]朱宁，李建军，李兵.一种有偏岭-压缩组合估计的新形式[A].曾玲，刘克.第八届中国青年运筹信息管理学者大会论文集[C]桂林：桂林电子科技大学，2006.

[6]Allen D M.Mean Square Error of Prediction As A Criterion for Selecting Variables[J].Technometrics,1971,(13).

[7]张尧庭，方开泰.多元统计分析引论[M].北京：科学出版社，1982.

[8]Andrews D F,Pregibon D.Finding The Outliers That Matter[J].J.Roy.Statist.Soc.B,1978(40).

[9]Draper N R,John J A.Influence Observations and Outliers in Regression[J].Technometrics,1981,23(1).

[10]Cook R D.Detection of Influential Observations in Linear Regression[J].Technometrics,1977(19).