IRT框架下的缺失过程建模及其Bayes估计方法

付志慧，李 斌，李晓毅，彭毳鑫

（1.沈阳师范大学 数学与系统科学学院，沈阳 110034；2.吉林师范大学 外语部，吉林 四平 136000）

0 引言

另外，在似然基本结构中，参数ζ和θ需是已知的。如果缺失数据是随机缺失（MAR）且是确定的，那么缺失数据就是可以被忽略的。所以在似然基本推断中，如果缺失数据是MAR，那么缺失数据机制或过程是可忽略的。这意味着，在分析过程中我们可以不用考虑ζ还能够保证我们得估计结果是不变的。而Bayesian过程中，在缺失数据是MAR且θ与ζ的先验是独立的条件下，缺失数据机制是可忽略的。

在教育测量中，有时候不反应项目是不可忽略的。例如，有时间限制的测试中，能力低的测试者不能答到最后，缺失数据的模式与被测试者的能力有关，因此缺失数据是不可忽略的。

处理缺失数据有四种方法[2,3]。

第一种，在做统计分析前先删除缺失数据，这种删除数据的方法偶尔是合适的，但这种方法存在它的弊端，这种尝试会导致减少样本的大小使估计是无效的，如果缺失数据是系统的或者与我们的结果相关联，删除数据会使估计是有偏的[4]；

第二种，填补法。简单填补和多重填补。简单填补是指对于每一个缺失数据给一个替代值，再按照完全数据来处理；多重填补法是指以一系列随机值来替代缺失值，来保证缺失数据的随机性[5,6]。

第三种，忽略缺失数据，利用所有合适的可观测数据进行估计，这种方法存在的问题是对软件要求很高，需要能够处理很复杂的计算问题[7]；

第四种，明确地模拟引起缺失数据的机制，将观测数据拟合模型和附加模型合并[8-10]。

本文采用第四种方法，引入缺失模型。用一个二值项目反应模型来拟合缺失机制[11,12](Moustakiand Knott,2000；Holman and Glas,2005）,目的是处理项目反应理论中不可忽略的缺失数据参数估计问题。分别采用2PLM模型和Rasch模型来拟合观测数据和缺失指标。通过MCMC中的Gibbs抽样方法，对数据进行扩充，将较为复杂的后验密度转化成满条件分布，在此基础上，给出参数的Bayes后验估计。

培育现代竹产业园区。对符合条件的竹产业园区进行培育，并纳入到省级现代农业(林业)示范园区中，择优推荐申报国家林业产业示范园区。2015年四川创建的青神竹文化创意产业园成为四川省首个成功创建全国版权示范园区(基地)的县(区)域。

1 缺失过程建模

设X为二维数据阵，矩阵元素Xik表示被试i对项目k的反应变量；定义与反应阵相同的指示阵D，当Xik有观测时，其元素dik=1；当 Xik缺失时，dik=0，其中i=1，…，N，k=1，…，K 。 观 测 数 据 的 测 量 模 型 为p(xik|dik，θi，αk，βk)，是观测变量关于缺失数据指示变量指标、潜变量θ和项目参数的条件概率。当数据缺失时，Xik的条件分布为退化分布，p(Xik=xik|dik=0，θi，αk，βk)=1；当dik=1时，采用2PLM对其建模，被试i对项目k的正确反应概率为：

其中ζi为缺失过程的潜在变量，δk为缺失过程的难度参数。

在MAR模型中，似然函数为：

其中，g(·)是 ζi和 θi的密度函数，来自于一个多元正态分布，均值为0，斜方差阵为Σ。

我们采用Bayesian对（3）和（4）进行参数估计。Beguin（2001）和Glas(2005)给出了模型识别的方法，从他们的结论可知，通过基底变换，可以使观测数据模型和缺失数据指示模型依赖于相同的两个潜在变量。因此，在这个模型框架下，这两个潜在变量是函数相依的。

2 不可忽略IRT模型的MCMC估计方法

MCMC方法的基本思想是通过建立一个平稳分布为π(x)的Markov链来得到π(x)的样本，基于这些样本就可以做统计推断。最简单、应用最广泛的MCMC方法就是Gibbs抽样。本文利用Gibbs方法来建立马氏链。在Gibbs抽样的构造之初，先将参数分成几个分量，依次给定其他分量，对每一个分量关于满条件分布抽样。

令 λ=(θ，ζ，α，β，δ，μ，Σ)为模型中所有未知参数分量的集合，λ的后验分布为

引入潜在变量Uik和Vik，对应于第i个被试在第k个项目上的反应变量Xik和缺失数据指示变量dik，潜在变量服从均匀分布U(0，1)，Xik与Uik之间满足如下关系：

Xik=1当且仅当Uik≤Φik

第三步：抽取η。

通过以上五步，我们完成了所有参数满条件分布的抽取。利用Gibbs抽样的优势，除去参数u，Σ外的所有参数的满条件分布都是相应先验的截尾分布。给定参数初值，进行迭代，从上述分布中抽取样本U，V，β，δ，η，α，μ，Σ。但要注意的是，所有的抽样分布都是以缺失数据指示阵D为条件的(详细程序由MATLAB编写)。

3 模拟研究

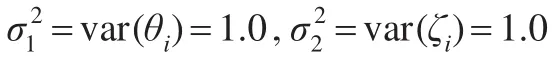
利用生成的数据，对随机缺失模型和非随机缺失模型进行项目参数的Bayes估计，利用Geman-Rubin方法进行收敛性诊断。进行如下操作：调试期n0=4000，迭代次数为20000次，重复进行模拟实验20次。比较实验结果υ^(r)，r=1，…，20和参数真值，两者之间差异越小说明估计方法越有效。选取统计量偏差，表达式为：

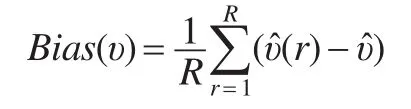
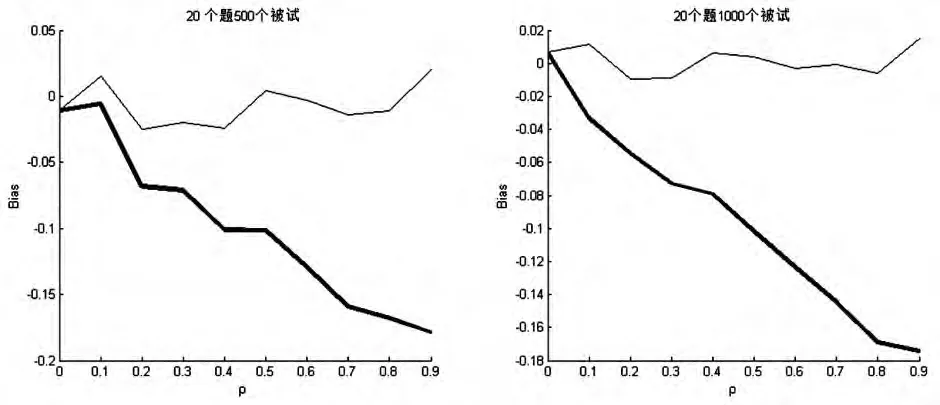
图1 Bias(β′)（细线）及Bias(β )（粗线）在不同 ρ下取值的比较

4 结论

近年来，缺失数据的处理方法很受统计学家的重视，相关文献很多。在IRT框架下，大部分研究主要还是处理可忽略缺失数据，对于不可忽略缺失问题，Holman&Glas提出采用边际最大似然法给出估计，然而该方法要受积分维数的限制。本文针对二参数Logistic模型，通过对缺失指标进行建模，采用一种简单灵活的Gibbs抽样方法给出了模型参数的Bayesian估计。通过模拟易见，对于不可忽略缺失数据，如果将其忽略掉(采用MAR(3)模型估计),会给项目参数估计带来很大偏差，而且观测数据模型中的潜变量和缺失指标模型中的潜变量之间的相关度越高，偏差越大；进一步地，模拟表明采用NONMAR(4)估计，偏差大大减少。另外，该方法还可以推广到含有协变量的缺失模型及多层反应模型中。

[1]Beguia A A,Glas C A W.MCMC Estimation and Some Model-Fit Analysis of Multidimensional IRT Models[Z].Psychometrika,2001,(66).

[2]Little R J A,Rubin D B.Statistical Analysis With Missing Data.2nd ed.(Sun,S Z,Trans.)[Z].New York:John Wiley&Sons,2004.

[3]Rubin D B.Inference and Missing Data[C].Biometrika,1976,(63).

[4]Karkee T,Finkelman M.(April).Missing Data Treatment Methods in Parameter Recovery for A Mixed-Format Test[J].Paper Presented at The Annual Meeting of The American Educational Research Association,Chicago,2007.

[5]Gelman A,Rubin D B.Inference From Iterative Simulation Using Multiple Sequences(With Discussion)[J].Statistical Science,1992,(7).

[6]Huisman M.Imputation of Missing Item Responses:Some Simple Techniques[J].Quality and Quantity,2000,(34).

[7]Muraki E,Bock R D.IRT Based Test Scoring and Item Analysis For Graded Open-Ended Exercises and Performance Tasks[J].Chicago:Scienti-C Software Int,1993.

[8]Moustaki I,Knott M.Weighting for Item Non-Response in Attitude Scales By Using Latent Variable Models With Covariates[J].Journal of The Royal Statistical Society,2000,(163).

[9]汪金晖,张淑梅,辛涛.缺失数据下等级反应模型参数MCMC估计[J].北京师范大学学报(自然科学版)，2011,47(3).

[10]曾莉,辛涛,张淑梅.2PL模型的两种马尔科夫蒙特卡洛缺失数据处理方法比较[J].心理学报，2009,(41).

[11]Holman R,Glas C A W.Modeling Non-Ignorable Missing-Data Mechanism With Item Response Theory Models[J].British Journal of Mathematical and Statistical Psychology,2005,（58）.

[12]付志慧.多维项目反应模型的参数估计[D].吉林大学,2010.