基于区位熵的区域产业集聚度统计检验

刘文华 ，黄 鑫

（1.中山大学 管理学院，广州 510641；2.湖南工学院 经济与管理学院，湖南 衡阳 421002；3.湖南科技职业学院 陶瓷学院，长沙 410004）

0 引言

区位熵被广泛运用于测度区域产业集聚程度。区位熵长期以来被用于估计地区经济影响和出口活动的大小。通常运用就业数据，这一测度主要是两种份额的比率：某一地区的某个产业的就业份额与经济体内这一产业的就业份额。这种测度方法尽管广泛使用，但缺乏坚实的理论和统计基础的支撑。

产业集聚指标应该提供一个统计显著性结果。现有文献还没有就测度地区产业集聚程度的区位熵指标给出相应的统计检验的估计量。因此，本文试图在区位熵E-G指标构造为一个估计量，并提供相应的点估计的统计检验。最后，本文运用这一方法对2012年广东省制造业的产业集聚度进行了测度。

1 区位熵统计量的构造

根据Figueiredo et al.（2007），有J个不同的地区，假设某一特定产业k内企业的空间分布反映了其利润最大化对应的区位选择。对于产业k内的企业i，如果将区位选择于 j地区，此时的其利润表示为：

其中，πˉj反映了区域 j的所有产业的利润均值；ηik为某一地区对于某个特定行业k而言，存在的外部经济或自然优势的强度。一种测度ηik的方式是Ellison and Glaeser(1997)提出的：初始阶段，自然将资源禀赋分配给每个地区，这在对不同产业的利润的影响是不同的。另一方测度方法是Ellison et al.（2007）提出的，假设ηik反映了马歇尔外部性理论中这类内生性要素的优势。例如，地区某种技能性劳动力的可获得性或产业特定知识的存在性。最终，当企业做出区位选择决定时，他们将产业或地区的特定优势视为给定的，并且明白单一个体的决定并不会影响ηik。因此，从建模的角度，我们可以假设ηik是由某一随机机制产生的，并且企业服从某一分布。如我们将要看到的，区位熵可以理解为这些测度的一个估计量。最后，方程（1）是一个随机效应模型，可以捕捉到所有其他影响单个企业利润的异质性因素。通常来讲，我们假设εijk是独立同分布的，服从极值第一型（Extreme Value Type I）分布。我们可以利用MacFadden's（1974）的方法得到产业k内某一企业选择区位于地区 j的概率：

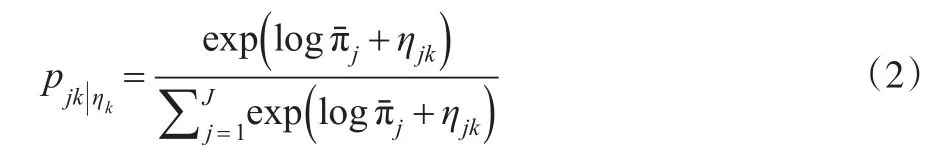
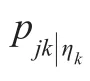
其中，xj是地区 j的制造业总就业人数，x是经济体中的总就业人数。我们引入Figueiredo等(2007)中的另一个假设，即从平均来讲，ηjk的作用以如下的方式被消除：

由于这一假设对数据ηjk的生成过程存在某些限制，我们将区位概率重写为下面xj的形式：

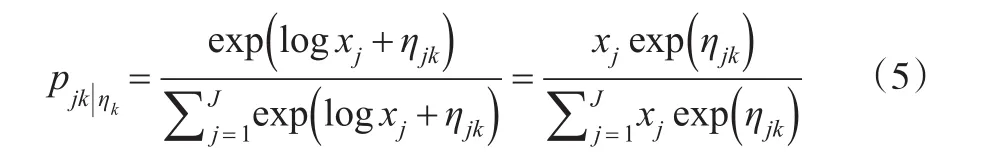
由于同一地区我们可以得到观察到的多重区位决策，我们将ηjk视为待估常量。为了更好的知道具体的操作，我们假设产业k存在nk个工厂，相应存在nk个独立的区位决策。这意味着，我们可以构建一个似然函数。由于产业的区位概率，似然函数服从特定的空间分布，并且每个区位用wjk进行加权。因此，给定部门的似然函数可以表示为：

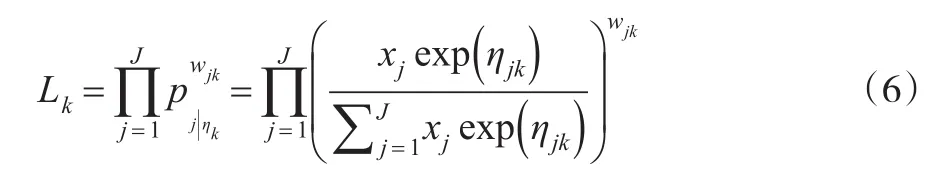
注意到，通过引入权重，我们可以考虑这一可能性：同一地区的两个区位决策，将为似然函数起到不同的作用。例如，可能存在的争议是，大企业的区位决策应该更重要。为了考虑这种情况，我们可以将权重设为就业或其他衡量的企业规模的相应比例。在任何一种情况下，如果考虑了权重，此时不同地区的总和wk，应标准化为产业内观察到的区位决策个数。

最大化方程（6）所表示的似然函数，此时最大化的一阶条件可以表示为以下形式：

由于ηjk是不可识别的，一阶条件将导致不确定性解的存在。为了解决这一问题，我们需要对参数引入约束。因此，为了识别的目的，我们引入这一约束条件：

此时，我们可以得到ηjk的度量标准。这一约束条件也具有直观含义。从式（5）可以看出，如果地区 j的参数ηjk等于0，这意味着实际的区位概率等于预期值，此时产业k将不会选择定位于地区 j。求解这一阶条件，我们可以得到下面的极大似然估计量：

此时，区位熵的推导可以视为从概率模型得到的估计量，为构建假设检验提供了可行的分析框架。需要注意的是，假设需要以ηjk的形式来构建；也就是说，未知变量需要捕捉到特定地区的区位优势。

2 基于区位熵的检验

考虑ηjk的线性组合的Wald检验一般形式：

其中，R是一个包含线性组合参数的矩阵，q是常数向量，φ是η的极大似然估计值，V是η的方差-协方差估计值。这一检验服从自由度等于检验约束条件数的卡方分布。为了计算V，我们利用负海赛矩阵的逆通过计算极大似然估计可以得到。利用一阶条件，我们可以将式（8）重写为以下形式：

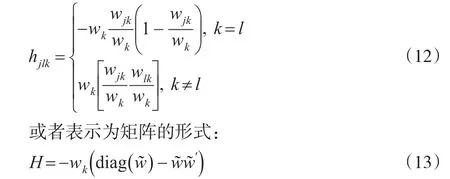
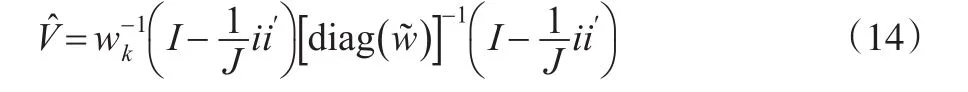
基于区位熵，另一检验是假设ηjk对于所有的地区都是相同的。如果假设是成立的，那么所有的产业的区位概率和每个地区的制造业就业份额是相同的。为了进行这一检验，用φr来代替原假设下φ的值。此时，Rao's score检验可以通过下面的统计量得到：

以上统计量渐近服从自由度为J-1的卡方分布，并且具有直观的含义：如果区位熵都是1，那么产业的本地化程度为0；区位熵和1相差越大，本地化程度越高。

3 区位熵统计检验的实例：以广东为例

现在我们将上面的检验应用到我国的具体实例：考察广东省的产业本地化程度。改革开放以来，中国成为了世界工厂，而广东又是我国的制造业中心。因此选择广东作为本文的研究样本具有代表性。同Guimarães et al.（2009），我们也采用就业数据来衡量区位熵。

我们将回答以下几个问题：

（1）和全国平均水平相比，是否有制造业部门本地化于广东省？

（2）如果是这样，这一部门是否本地化于广东省内部的某个地级市？

（3）本地化于哪个地级市？

为了回答以上答案，我们需要我国31个省级的就业数据以及制造业企业数据，以及广东省内部的各个地级市的数据。在表1中，我们给出了计算得到的省级层面的产业区位熵。区位熵的计算，是根据《国民经济行业分类GB/T 4754-2011》标准，四位编码上对应有34个制造业部门，即对应到中类。我们发现，有24个行业的区位熵高于1。

我们将区位熵大于1的产业挑选出来，并采取上文的统计量进行检验，结果见表2所示。

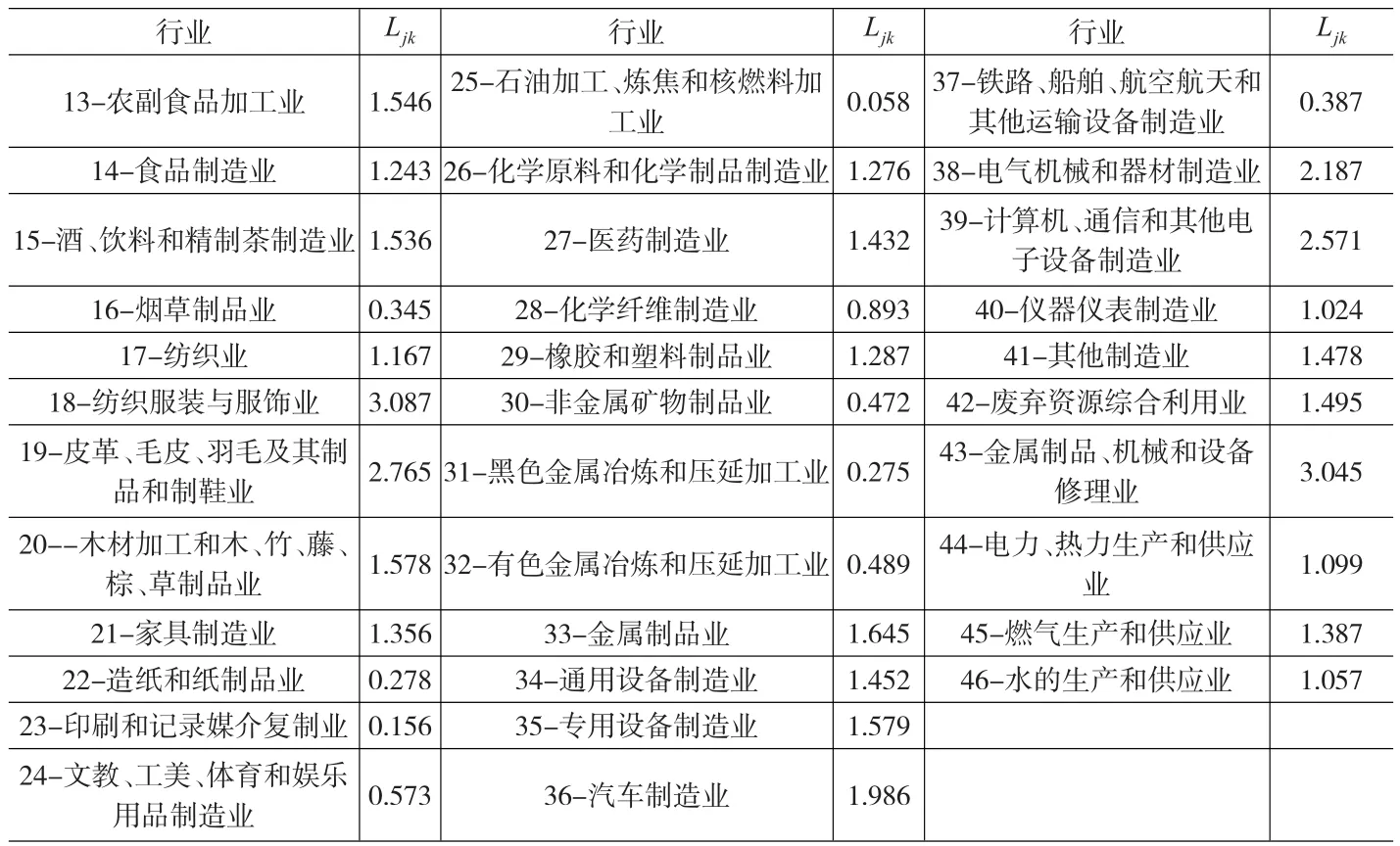
表1 2012年广东省制造业区位熵

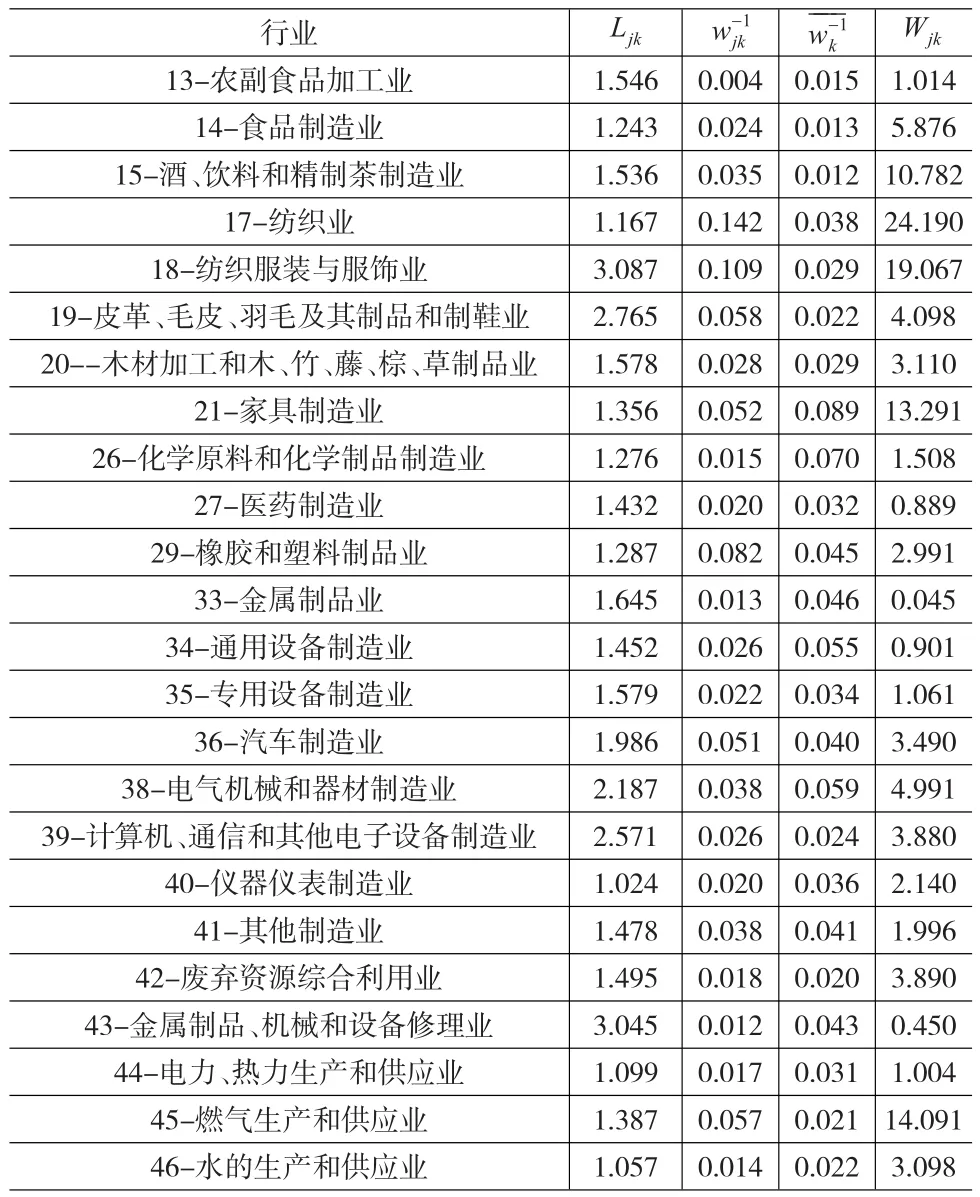
表2 区位熵及其检验

我们利用式（15）中的统计量来检验区位熵是否反映了产业的地理临近。由于统计量渐近服从自由度为1的卡方分布，因此单边检验时5%的显著性水平对应的临界值为2.71。在表2中可以看出，24个行业中有14个行业通过了显著性检验，具体包括：食品制造业、酒、饮料和精制茶制造业、纺织业、纺织服装与服饰业、皮革、毛皮、羽毛及其制品和制鞋业、木材加工和木、竹、藤、棕、草制品业、家具制造业、橡胶和塑料制品业、汽车制造业、电气机械和器材制造业、计算机、通信和其他电子设备制造业、废弃资源综合利用业、燃气生产和供应业和水的生产和供应业。我们可以认为，上述14个行业本地化于广东省。

接下来，我们将检验区位熵显著性水平最高的纺织业是否本地化于广东省内部。为了回答这一问题，我们计算了纺织业在广东省地级市层面的区位商。由于统计量渐近服从自由度为J-1的卡方分布，此时5%的显著性水平对应的临界值为14.07。通过计算得出，纺织业在广东省地级市层面的区位熵为41.09，通过了5%的显著性检验。因此，我们有理由相信纺织业是本地化于广东省内部的。

最后，在表3中，我们将回答最后一个问题：在广东内部，纺织业本地化于地区？为了得到这一结果，我们再次利用方程（15）进行检验。

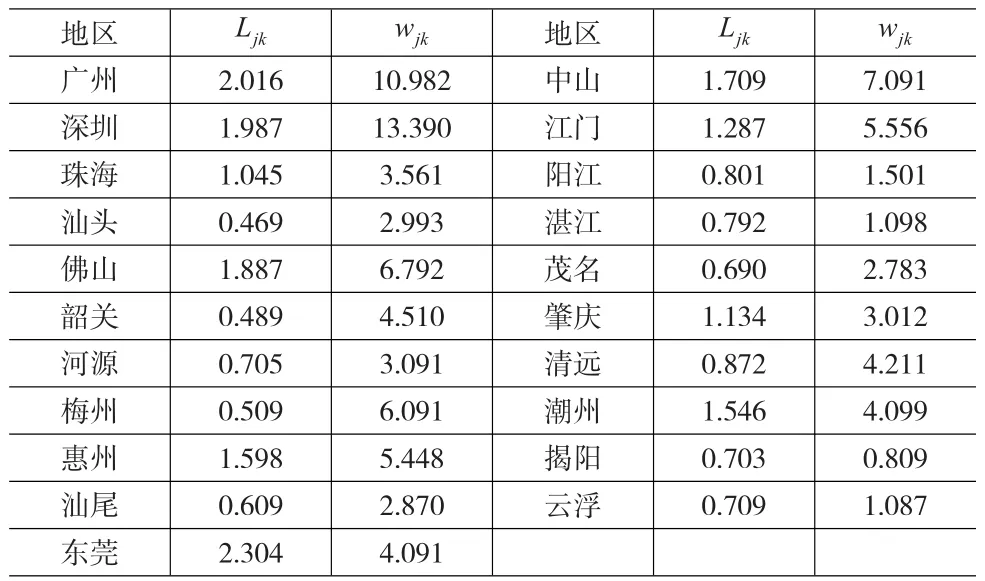
表3 2012年广东省内部纺织业本地化

根据表3的结果，广东省的纺织业区位熵大于1的地区有广州、深圳、珠海、佛山、惠州、东莞、中山、江门、肇庆、潮州。其中，区位熵最大的东莞，达到2.304，其次是广州，达到2.016。并且区位熵大于1的地区，都通过了5%的显著性检验。这表明，广东省的纺织业本地化于东莞地区，也说明了纺织业在广东省内部也存在本地化现象。

4 结论

在经济学中，区位熵被大量运用于测度产业集聚程度。研究者通常假设，如果区位熵大于1，则产业集聚在某一特定地区。然而，这一分析思路存在较大的问题：缺乏任何合适的统计标准来判断这种测度方法是否能够反映产业的地理集中程度。因此，尽管区位熵方法在实践中被大量采用，但却缺乏理论基础。特别的，这种方法不能解释潜在区位选择的内在随机性。

本文在Ellison and Glaeser（1997）的基础上，将传统的就业区位熵构建成一个估计量。这一方法具备的最大优势是，可以在估计区位熵的同时提供一个统计检验的基本框架。因此，这可以解释统计推断中抽样的不确定性。统计或估计参数而没有给出相应的显著性水平，会因缺乏精确性而影响其应用价值。因此，今后使用区位熵测度区域产业集聚度时，在报告点估计量时需要给出相应的统计检验值。

[1]池建宇,姚林青.北京市文化创意产业集聚效应的实证分析[J].中央财经大学学报,2013,（8）.

[2]樊秀峰,康晓琴.陕西省制造业产业集聚度测算及其影响因素实证分析[J].经济地理，2013,（9）.

[3]杨仁发，产业集聚与地区工资差距——基于我国269个城市的实证研究[J].管理世,2013（8）.

[4]杨丽华.长三角高技术产业集聚对出口贸易影响的研究[J].国际贸易问题，2013,（7）.

[5]周凯,刘帅.金融资源集聚能否促进经济增长——基于中国31个省份规模以上工业企业数据的实证检验[J].宏观经济研究，2013,（11）.

[6]Duranton G,Overman,H.Testing for Localisation Using Micro-geographic Data[J].Review of Economic Studies,2005,72(4).

[7]Ellison G,Glaeser,E.Geographic Concentration in U.S.Manufacturing Industries:A Dartboard Approach[J].Journal of Political Economy,1997,105(5).

[8]Ellison G,Glaeser E L,Kerr W.What Causes Industry Agglomeration?Evidence from Coagglomeration patterns[R].NBER Working Papers,No.13068,2007.

[9]Figueiredo O,Guimarães P,Woodward D.Localization Economies and Establishment Scale:A Dartboard Approach[J].FEP Working Paper,2007.

[10]Guimarães P,Figueiredo O,Woodward D.Measuring the Localization of Economic Activity:A Parametric Approach[J].Journal of Regional Science,2007,(4).

[11]Tanabe K,Sagae,M An Exact Cholesky Decomposition and the Generalized Inverse of the Variance-covariance Matrix of the Multinomial Distribution,with Applications[J].Journal of the Royal Statistical Society,Series B,1992.