基于RBF神经网络非线性集成模型的天然气需求预测

冯 雪，张金锁，邹绍辉，包乌云毕力格

（西安科技大学a.能源经济与管理研究中心；b.管理学院；c.能源学院；d.通信学院,西安 710054）

0 引言

21世纪初全球经济的高速发展、持续的高油价以及日益严格的环保要求为天然气产业发展提供了历史性机遇，天然气市场蕴藏广阔的发展前景[1]。准确分析和预测天然气需求量既有利于保障能源供需平衡和规避能源供给风险，也是指导国内能源产业结构调整，加快转变经济发展方式，促进我国经济社会可持续发展的需要。

国内外在能源需求预测方面的研究起步较早，已取得了丰硕的成果，但我国天然气需求预测的文献相对较少。从文献梳理看出，已有组合模型虽然较好地克服了单一预测模型的缺陷，但仅对模型组合方式进行改善和优化，没有紧扣研究对象的数据特征进行有针对性的研究，预测精度也有待提高。我国学者汪寿阳[2]在这方面有所突破，利用TEI@I（文本挖掘“Text mining”+经济计量“Econometrics”+智能技术“Intelligence”@集成技术“Integration”）方法论的思想提出非线性集成预测模型，对非线性程度高、波动性强（通常由不规则事件导致）的外汇汇率进行实证研究，结果表明该方法不仅适用性强，且预测效果相较组合模型大幅提高。本文借鉴TEI@I方法论思想，针对我国天然气消费数据呈现的低波动、非线性趋势特征，利用非线性集成模型对我国天然气需求进行预测，以实现预测结果的高精度和科学性。

1 建模思路及主要模型简介

1.1 非线性集成模型建模思路

非线性集成模型建模思路在于：首先，围绕我国天然气消费数据特征，通过线性模型拟合天然气需求的主要确定性趋势，用非线性模型对其残差序列进行修正，以捕捉其非线性与不确定性的特征，从而构建组合模型；其次，分别利用线性模型和非线性模型来拟合并预测天然气需求的整体趋势，得到两个单一预测模型；最后，选取RBF神经网络作为集成工具，非线性集成前述三个模型的拟合结果，由此建立基于非线性集成模型的我国天然气需求预测模型，总体思路如图1。

图1 基于非线性集成模型的我国天然气需求预测思路

1.2 模型简介

在线性和非线性模型的选取上，考虑到ARIMA模型适用于任何平稳和线性的时间序列，且预测效果较好，而RBF神经网络针对非线性关系具有较强的挖掘和拟合能力，并且其具有较强的网络学习能力和泛化能力，预测精度较高[3，4]。因此，本文根据天然气需求平稳、线性与非线性混合的特征，选用ARIMA模型拟合其平稳、线性趋势，选用RBF神经网络模型作为残差修正技术、非线性预测技术和非线性集成技术。

ARIMA模型原理：该模型适用于平稳时间序列，因此需要对具有某种趋势或循环特征的时间序列xt进行平稳性检验，若时间序列不满足平稳性要求，可以通过d阶差分后达到平稳性，此时可用ARIMA模型建模，最后对预测结果进行逆转换得到原序列的预测值[5]。ARIMA模型的数学表达式如式（1）：

其中，△dxt是原序列xt经d次差分后得到的平稳序列。θ0是t时刻的随机误差。Φi（i=1，2，…，p）和θj（j=1，2，…，q）为该模型的待估参数，p和q是模型阶数。该模型记为ARIMA（p，d，q）。

RBF神经网络模型原理：RBF神经网络属于前馈网络，结构分为三层，即输入层、隐含层和输出层，主要有以下两阶段的学习过程[6]：（1）通过输入样本来确定隐含层j各节点的径向基函数中心值cj和径向基函数宽度σj。（2）隐含层j参数确定之后，由最小二乘法求得输出层权值wj。根据研究需要，可以在第二阶段之后，利用样本信号，同时校正隐含层和输出层的参数，从而进一步提高精度。RBF神经网络模型的核心环节在于迅速并高效地确定第一阶段的径向基函数中心值cj和第二阶段输出层权值wj。

2 实证分析

2.1 数据来源及预测评价

能源需求是指在一定时期内和一定条件下消费者能够且愿意购买的能源产品的数量。由于能源需求和能源消费有细微的差别[7]，本文在对天然气需求进行分析时，采用《中国统计年鉴》公布的天然气消费总量数据。对RBF神经网络所有的输入数据首先通过式（2）做归一化处理，将1985～2003年的归一数据作为网络训练样本来建立模型，2004～2012年的数据作为测试样本来检验模型。平均相对误差（MAPE）作为准则来评价预测性能，评价准则定义如式（3）。

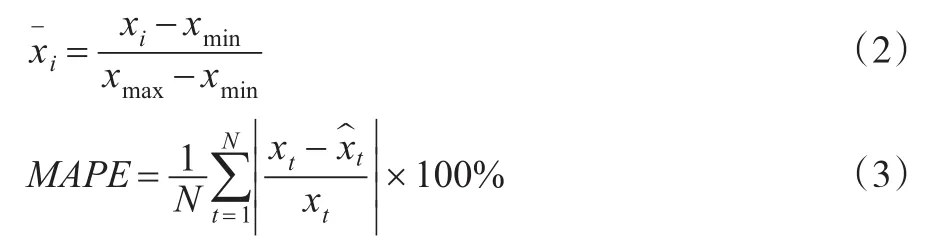
2.2 实证分析

2.2.1 ARIMA模型

经过异方差检验、ADF和PP检验发现，天然气需求量序列{Xt}存在异方差，且非平稳。对天然气需求量数据进行对数转换以消除异方差性，即令Yt=ln（Xt），再经过一次差分后进行平稳性检验。表1显示，{Xt}序列的ADF检验统计量（-1.095823）大于1%、5%、10%显著性水平的临界值，说明{Xt}是非平稳的。而经对数处理后的一阶差分序列{Zt}均在99%的置信水平下通过ADF检验，因此{Zt}为平稳时间序列。

由Zt=Yt-Yt-1确定ARIMA（p，d，q）模型参数d=1。根据AIC信息统计量准则[8]，当p=1，q=4时，模型滞后多项式倒数根都落入单位圆内，满足过程平稳的基本要求，调整后的 R2（0.596056）最 大 ，且 模 型 AIC（-2.887723），SC（-2.642295）值最小，意味着滞后阶数是较为合适的。初步确定ARIMA（1，1，4）为平稳序列{Zt}的最佳预测模型。用极大似然估计得到ARIMA（1，1，4）模型中所有参数值，模型估计为：

表1 {Xt}、{Yt}、{Zt}单位根检验结果

2.2.2 RBF神经网络残差修正模型

能源需求系统是个复杂系统，天然气的需求量受到国民经济增长、能源政策、人口等各种因素的影响，不可避免呈现非线性特征，这就限制了ARIMA模型针对非线性问题预测的准确性。各种影响因素导致的非线性影响反映在其残差序列中，则通过RBF神经网络模型来修正残差序列以进一步提高预测精度。

在预测残差序列时，采用滚动神经网络预测模型建立有效的学习样本。根据上述建立的RBF神经网络预测方法，确定RBF神经网络的输入节点数为16，输出节点数为1，中间层节点数为4。经过对样本的学习及仿真训练，得到残差序列拟合值，将其与ARIMA模型预测结果相结合形成新的组合预测值，如表2所示。相应的拟合曲线见图2。

2.2.3 RBF神经网络模型

使用RBF神经网络单独对整个天然气消费序列进行预测，RBF网络结构确定为16×4×1。通过MATLAB软件运行，隐含层神经元个数为4时训练次数为18，精度为3×10-3。反归一化处理后的预测计算结果如表2所示，相应的拟合曲线见图2。

2.2.4 RBF神经网络非线性集成拟合结果及对比分析

将ARIMA模型拟合值、RBF神经网络模型拟合值、ARIMA和RBF神经网络组合的拟合值，作为RBF神经网络的输入，通过RBF神经网络进行非线性集成。网络结构确定为16×4×1。通过MATLAB软件运行，得到非线性集成拟合结果如表2所示，相应的拟合曲线见图2。

从图2中可以直观地看出，非线性集成模型拟合值与实际值最为接近，拟合优度最好，其次是ARIMA模型、RBF神经网络残差修正后的组合模型，而RBF神经网络单独拟合效果最差。表2中的MAPE数据也验证了相同的结果。非线性集成模型的MAPE最小（2.81%），其次为ARIMA模型（3.55%），均明显高于RBF误差修正后的组合模型（6.78%）和RBF模型（9.00%），因此非线性集成模型的预测精度最高。ARIMA模型的预测精度高于RBF神经网络及其组合模型的预测精度，可能是因为天然气总体需求趋势非线性、波动性程度不高，在天然气需求预测方面，线性模型比非线性模型以及组合模型更为适合。而非线性集成模型抓住了以线性趋势为主，非线性趋势为辅的共同特征，在天然气需求预测研究上取得了显著的优势。另外，从2004～2012年各模型的相对误差来看，非线性集成模型相对误差波动性最小，趋势相对平稳，也说明该模型稳定性最强。

表2 单一模型和非线性集成模型预测值 （单位：万吨标准煤）

图2 各模型拟合图

总体来说，无论从预测精度还是稳定性来看，本文利用的非线性集成模型都是最优的，说明这个集成模型是成功的。

2.3 2013～2015年我国天然气需求量预测

表3 2013～2015年天然气需求量预测 （单位：万吨标准煤）

通过非线性集成模型预测出2013～2015年我国的天然气消费量（表3），同时给出其他三种预测模型的预测值进行对比。通过预测结果可以看出，2013～2015年我国天然气需求量以年均12.45%的比例增长，这种增长趋势对改善我国能源结构，实现低碳目标更加有利。

3 结论

集成模型相对误差4.77%2.53%0.50%1.52%6.17%5.45%1.56%2.37%0.39%2.81%

本文利用非线性集成模型对我国天然气需求进行拟合和预测。通过RBF神经网络技术，将单一的ARIMA模型预测值、RBF神经网络模型预测值以及RBF残差修正的组合模型预测值进行集成，构建出非线性集成预测模型。该模型吸取了各单一模型和组合模型的优点，克服了线性模型和非线性模型独立运用时信息遗漏的缺陷，改善了传统组合模型中权重系数主观性强、不易确定的状况，取得了较好的预测效果。

比较发现，非线性集成模型预测值的平均相对误差最小（2.81%），均明显高于单一的ARIMA模型（3.55%）、RBF残差修正后的组合模型（6.78%）和单一的RBF模型（9.00%）。非线性集成模型对我国天然气需求预测精度最高，稳定性最强，是对我国天然气需求预测地成功运用。预计2013～2015年我国天然气需求量以年均12.45%的比例增长，这种增速有利于我国能源消费结构的改善。

[1]国家统计局.中国国民经济和社会发展统计公报[M].北京:中国统计出版社,2012

[2]汪寿阳,余乐安,黎建强.TEI@I方法论及其在外汇汇率预测中的应用[J].管理学报,2007,1(1).

[3]Park J,Sandberg I W.Universal Approximation Using radial-basis-Function Networks[J].Neural Computation,1991,3(2).

[4]孙廷容,杨菊香,张洪波等.基于径向基函数网络的能源消费量预测模型[J].西安理工大学学报,2006,22(2).

[5]Box G,Jenkins G,Reinsel C.Time Series Analysis:Forecasting and Controlling[M].Englewood Cliffs,N J,USA:Prentice-Hall,1994.

[6]Powell M J D.Radial basis functions for multivariable interpolation:a review[C].IMA Conference on Algorithms for the Approximation of Functions and Data,Shrivenham:Royal Military College of Science,1985.

[7]Bhattacharyya.S C.Energy Economics[M].London Dordrecht Heidelberg New York,Springer,2011.

[8]Akaike H.Canonical Correlation Analysis of Time Series and the Use of an Information Criterion,in Systems Identification:Advances and Case Studies[M].New York:Academic Press,1976.