车辆极限荷载效应外推离散性分析及原因探究
严博翀
(上海东华地方铁路开发有限公司,上海 200071)
车辆极限荷载效应外推离散性分析及原因探究
严博翀*
(上海东华地方铁路开发有限公司,上海 200071)
在中国,由于车辆荷载不断加重,很多公路桥梁已出现结构损伤甚至倒塌,因此,对结构运营安全状况进行评定至关重要。其中,在荷载效应计算方面,许多学者采用Rice理论分析效应超越界限率分布,且以Cremona提出的方法确定尾端最优拟合起点,以此计算极限效应值。本文主要针对该方法极限值计算结果存在的离散性问题展开研究,并探究该问题的产生原因,从而为极限荷载效应预测方法的进一步发展提供重要的理论参考。结果表明,该方法的主观性、样本的随机性以及样本量的差异都可以导致较为显著的最优起点以及极限效应计算值的离散问题。深入分析后发现,其主要原因与该方法中不恰当的K-S检验使用方式以及不恰当的效应超越率理论分布假设有关。
公路桥梁, 车辆荷载, 极限效应, 离散性问题
1 引 言
中国近些年,由于车辆荷载不断加重,很多公路桥梁已出现结构损伤,甚至导致整座桥梁瞬间倒塌。究其原因,固然与桥梁结构性能退化以及对超载车辆管理不周有关,但对车重以及交通量如此大的增长趋势预估不足也是主要原因之一。故如何准确评定现有桥梁运营安全状况,防止塌桥事故的再次发生就成为一个值得研究的课题。其中,交通车辆作为桥梁结构所受主要外部荷载之一,是结构安全评定的重要考虑因素。然而,此类荷载具有显著的随机特征,定量分析的难度较大。
相当数量的学者[1-4]采用Rice理论分析荷载效应超越界限率分布(效应超越界限率v(x)的统计方式见图1),并通过拟合分布的大值尾端来计算极限效应值。

图1 x1效应界限超越次数统计
在Cremona等[5-7]的研究之前,效应超越界限分布的Rice[8-9]公式(式(1))拟合范围或者说效应大值尾部的Rice公式拟合起点(阀值),都是按照经验来确定的。然而,拟合起点的不同选择对极限效应的计算结果影响不容忽视(图2),因此该问题亟待解决。
(1)
于是,Cremona[5]提出采用K-S检验法对尾端不同效应作为起点(图3中的x0)时的Rice公式拟合结果进行优度检验,从而确定最优拟合效应起点,并以此计算重现期荷载效应值。根据该优化方法,Cremona等采用WIM(Weigh-in-Motion)数据和影响面加载方式计算获得效应历程,并对一座斜拉桥由交通荷载产生的索力增量以及一座悬索桥上的车辆荷载总量等效应进行了外推分析。
该方法涉及超越率分布直方图的分组区间长度I(图3)、曲线拟合差异参数Dn(图4)以及对应的显著性水平α(式(2))。
(2)
至此,后续基于Rice公式计算极限荷载效应的研究[10-15]基本都采用此方法确定最优拟合起点(阀值)。

图3 超越率直方图尾部曲线拟合Fig.3 Tail curve fitting of crossing rate histogram

图4 K-S检验参数Dn
本文主要针对该方法极限值计算结果存在的离散性问题展开研究,并探究该问题的产生原因,从而为极限荷载效应预测方法的进一步发展提供重要的理论参考。
2 荷载效应历程计算
2.1 交通参量统计分析
本文根据中国107国道WIM测站采集的交通数据进行车辆荷载参量统计分析,结果见表1。除此以外,车间距参量则按照中国在20世纪末进行的大范围交通数据调研及研究结果[16]取值,见表2。
表1 各代表车型特征参数、交通量占比以及车重分布
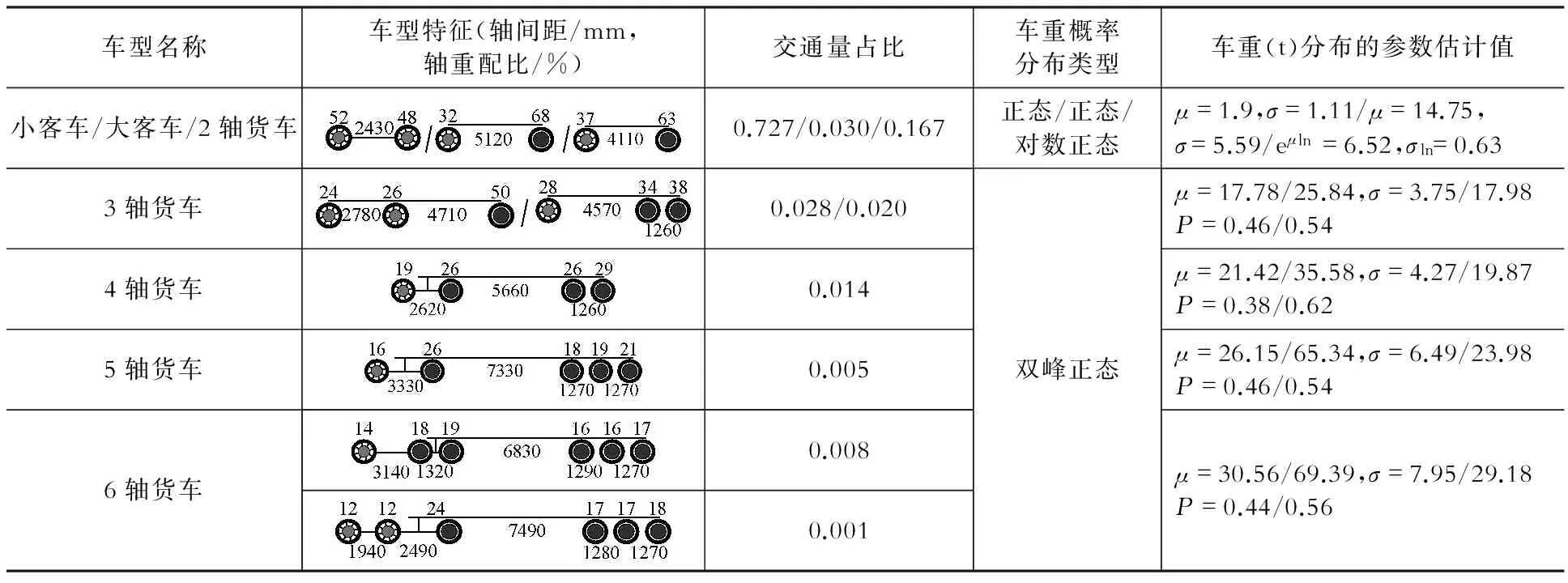
Table 1 Parameters of vehicle load spectrum
表2 车间距分布参数

Table 2 Distributed parameters vehicle interval
2.2 车流模拟及荷载效应计算
为增大分析数据的样本量,本文在交通参量统计分析的基础上,通过蒙特卡洛方法模拟交通车流,从而增大已有荷载数据量,其流程见图5。为简化分析,本文假定在车辆加载过程中,车间距保持恒定,并认为车辆过桥时间不变,从而对应时间轴刻度与车辆加载位置的关系。由此,将各车轴加载产生的效应历程按时间轴排列,然后对所有车轴在某一时刻产生的效应求和即可得到该时刻的总荷载效应(图5)。
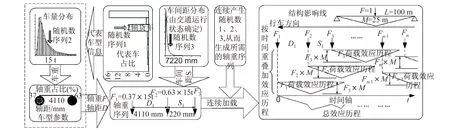
图5 车流模拟及荷载效应历程计算
3 极限效应离散性分析及原因探究
3.1 主观因素及样本随机性影响分析
3.1.1 离散性分析
以5年密集运行状态的虚拟车流为例,其在100 m简支跨中弯矩影响线上通行加载得到的荷载效应范围为0~53 230 kN·m(图6)。选取不同的效应间隔I(效应超越界限率分布直方图的分组区间长度),以确定需计数的离散效应值,并统计得到相应的超越率分布。图7所示内容为,采用不同效应间隔和不同显著性水平并根据Cremona方法确定的1年和2000年重现期效应外推值x1和x2000。
图7中的I值分别取为1 kN·m,3.5 kN·m,10 kN·m,35 kN·m和100 kN·m,相对最优的显著性水平α分别设为0.8,0.85,0.9,0.95和0.995。当I=35 kN·m时,所有相对最优拟合起

图6 5年交通加载计算的效应超越数分布
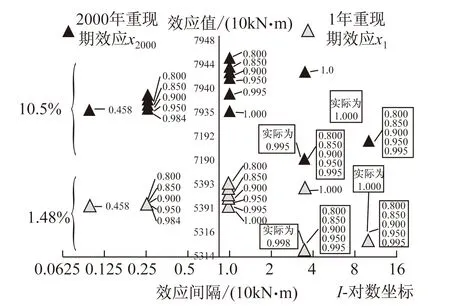
图7 由Cremona法计算的x1和x2000
点都为同一点,由此计算的重现期效应自然也是同一点,实际对应的α都为0.995;I=100 kN·m时,算出的最优起点结果也都为同一点,实际对应的α都为1;I=3.5 kN·m时,计算所得α的最大值为0.984,绝对最优未达到1;I=1 kN·m时,全部相对最优拟合α都未达到设定值,绝对最优的α为0.458。
由此可见,根据Cremona方法外推的重现期荷载效应会随着效应间隔I以及显著性水平α取值的变化而不同。5组数据间x1的最大差别达1.48%,x2000最大差别达10.50%。而随着I值以及α值选择范围的增大,外推效应的离散性也将进一步增大。与此同时,显著性水平α受效应间隔I的影响明显,即使所设α相同,也不能保证在任何I取值的情况下都能算得相应的重现期效应。
表3所示为各种计算情况中确定的效应阀值。从中可知,随着α和I取值的不同,最优拟合起点的最大差别可相差好几倍(7 500~31 000 kN·m),由此必然引起极限计算值的较大差别(图2)。
表3 最优拟合起点效应

Table 3 Optimal fitting thresholds
除效应间隔以及显著性水平对结果离散性的影响外,由于每次根据模拟或者实测的数据分析得到的效应超越率分布都只是一个样本,本身存在随机性,所以由此导致的结果离散性问题同样不容忽视。
图8所示为采用20组5年密集交通分别加载100米简支跨中弯矩影响线外推计算的不同重现期效应值(α和I都取相同值)。从中可以看出,根据具有相同车流特征和样本量的样本分析得到的极限效应值的变动范围较显著。计算表明,1年重现期效应值为48 500~53 400 kN·m,相差10.1%;1000年对应值为61 700~75 600 kN·m,相差22.5%。
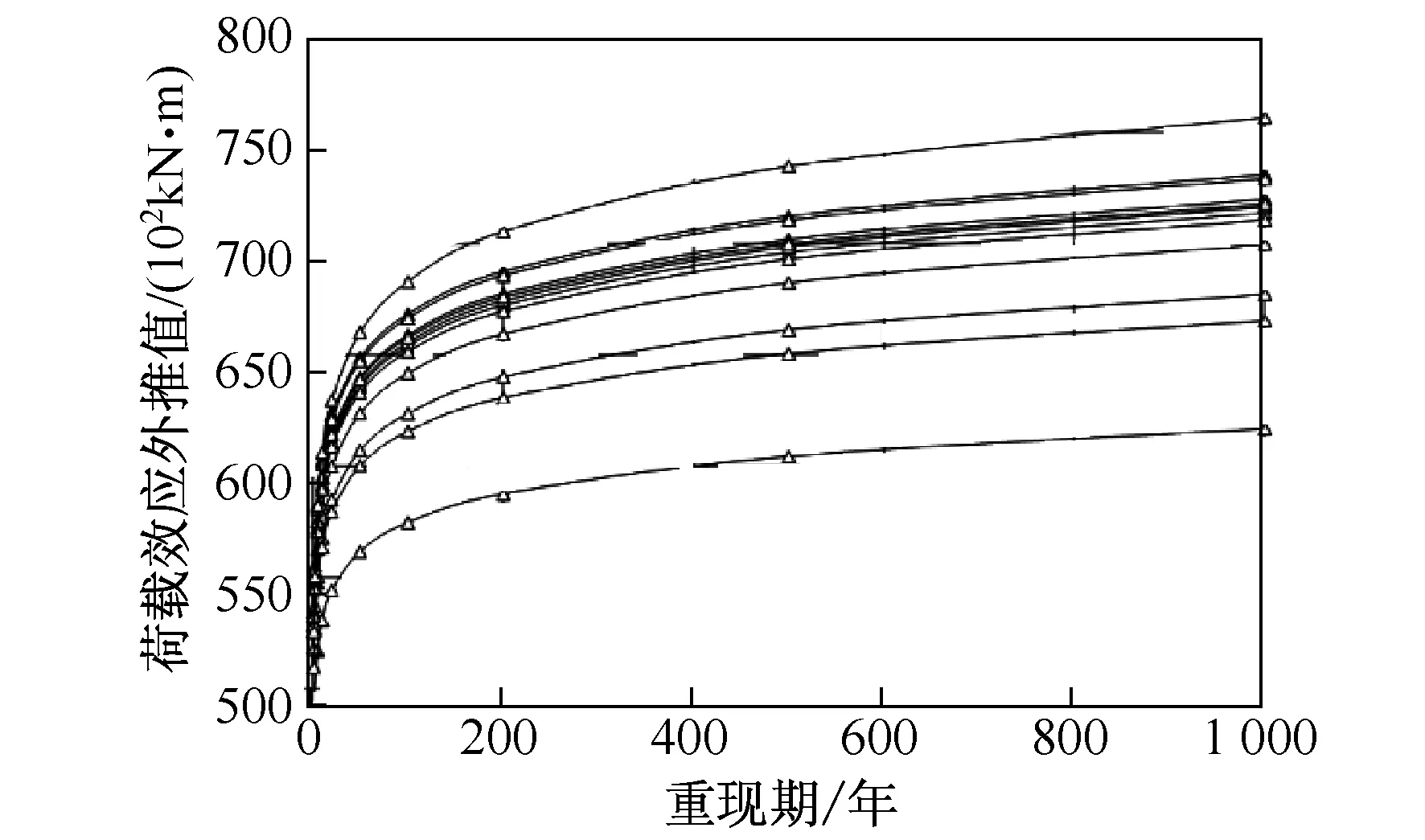
图8 基于不同样本分析得到的极限效应
3.1.2 原因探究
将分组区间取得特别小(1 kN·m),并采用超长时间(200年)交通流进行影响线加载以及荷载效应计算,由此将统计得到的样本分布近似作为荷载效应超越界限率的理论分布。
对一组确定的样本数据而言,K-S检验中的样本量n(图4)是定值,但Cremona方法将样本量近似取为拟合起点至尾端间直方图的分组区间数,这必然导致样本量的随意性,所以此处本文采用真正构成效应起点后超越率样本分布的上升幅作为样本,统计其样本量。
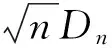
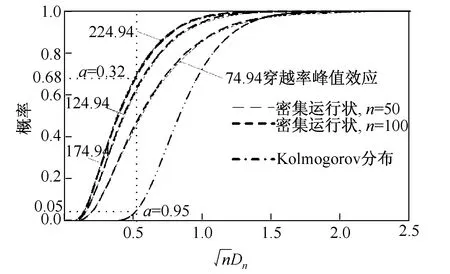

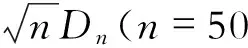
(3)
式中,K(x)为Kolmogorov分布,与分布函数FX(x)的具体类型无关。
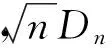
由此可以判定,Cremona方法所计算的α值(式(2))并不是真正的显著性水平,例如当计算所得α=0.95时,其实际值可能为0.32(图9),而Cremona方法中由主观确定的样本量则可能进一步导致α计算值对实际值的偏离。
通过上述分析结果便可解释Cremona方法中存在的两个显而易见的概念矛盾:
(2) 对某次模拟的一定时长的虚拟交通流而言,其作用下产生的效应超越界限率分布是确定的。分组区间(效应间隔)取的越细越能够完整体现整个超越率分布的形态,从而有利于极限效应的计算。但在用拟合范围内的效应直方数n′作为样本量n的近似值后,如果效应间隔划分得无穷细,即n趋于无穷大,或效应间隔I变得无穷小,则任何范围内的样本分布都无法通过关于拟合曲线优度的K-S检验,从而得不到任何计算结果。与此同时,n′值的随意性也导致α的计算值随I值的不同而变化明显。
3.1.3 问题纠正与改进
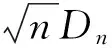
(4)
式中,ρ[n(xo)]表示均值修正系数,可按式(5)计算(详见图10)。
(5)
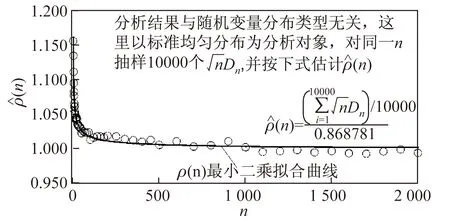
图10 ρ(n)均值修正系数
在实际交通中,前后车辆可视为互相独立的个体,它们的车型和车重互不相干,但是却在影响线范围内共同参与生成某一时刻的结构荷载效应,故相邻时刻的效应间连续变化,具有很高的相关性,而随着时刻间隔的增大,效应则逐渐趋于互相独立。为保证分析数据间的独立性,本文以影响线长为间隔抽取效应历程任意时点随机变量样本数据。

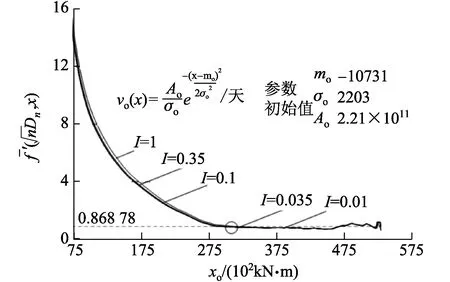

与此同时,根据不同效应间隔取值分析得到的曲线的变化趋势非常接近,基本都在xo超过31 300 kN·m之后进入最优拟合区段,由此体现出该改进的阀值确定方法的客观有效性。为此,下文分析以该改进方法替代Cremona提出的方法。
3.2 车流数据时长影响分析
3.2.1 离散性分析

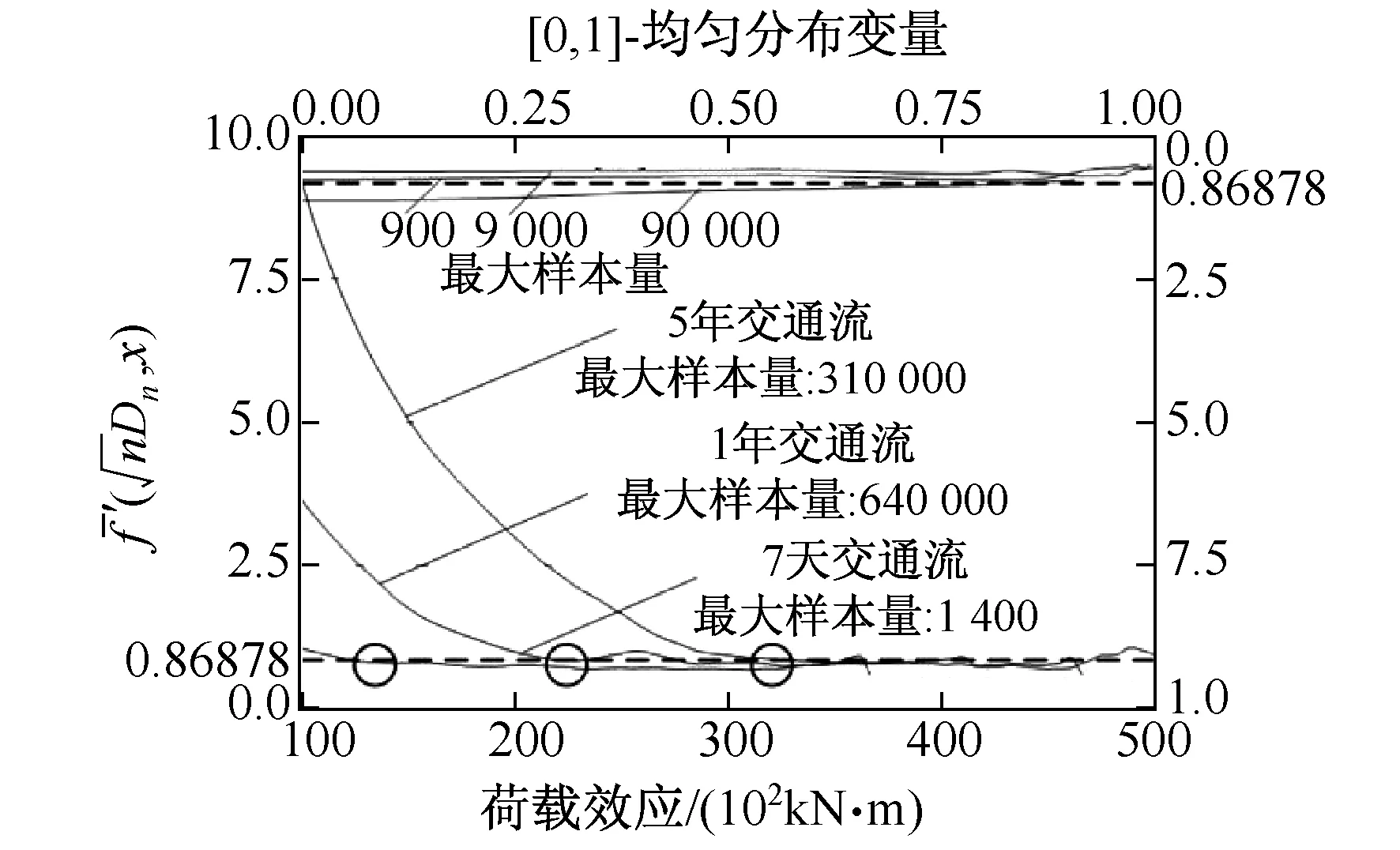

3.2.2 原因探究

为此,本文根据影响线范围内交通流的密集程度按极端密集、比较密集、极端稀疏以及其他共4种情况对尾端效应超越界限率的理论分布进行讨论。
1) 极端密集情况
此种类型往往对应超多车道,影响线较长且各车道交通流密度都较大的情况。此时,任意时刻的结构总效应等于各车道的效应求和,而各车道车流加载产生的平稳效应历程的任意时点变量各自服从一特定概率分布。由中心极限定理(独立但不同分布的变量和)可知,当车道数无穷大时,任意时刻的结构总效应趋于正态分布,从而总效应历程趋于高斯过程,其超越界限率分布符合Rice公式。各车道交通流密度越高,任意时刻的总效应收敛于正态分布的速度越快,所需的车道数也越少。
以5年的虚拟密集交通流加载100 m简支梁跨中弯矩影响线,计算不同数量车道同时加载时的总效应历程超越界限数分布。计算中假定各车道影响线和车流特征一致,计算结果如图13所示。该图结果表明,仅单车道加载时,超越数分布整体呈现出明显的单峰偏态,而随着同时加载车道数的增加,超越数分布的效应值逐渐增大,范围逐渐增宽,整体分布逐步趋于左右对称的单峰形式,即趋于正态分布形状。
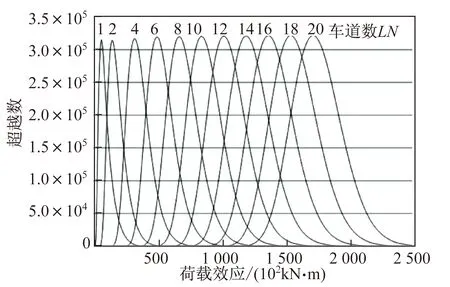
图13 多车道同时加载时的效应超越数分布
图13的分析结果虽然说明了Rice理论在极端密集交通情况下的适用性,但这种极端情况在实际中基本不可能出现,因为一方面不存在有那么多车道的桥梁,另一方面,要保证稳定的效应历程,车流同时作用的车道数量必须保持不变,而实际中当车道数特别多时,车道同时被占用的情况的发生比例非常小。除此以外,即使随着交通需求的增长,出现了超多车道的桥梁,那么由于所关注的荷载效应的横向车道影响范围有限,起主要作用的车道数并不会无限制增加,从而任意时刻的总效应与正态分布总存在比较大的差距。
2) 比较密集情况
为定量分析效应超越界限率分布的尾部效应到底是由多少车同时作用产生的,本文采用简化的单车等效均布荷载和平均车间距组成的车队加载影响线进行效应计算。计算中假设各车道同时作用相同车队,并取最不利效应值,结果如图14中的虚线所示。该结果表明,不同车队(车辆数不同)同时加载得到的荷载效应随着车辆数的增加而逐渐增大,越来越靠近相应超越数分布的峰值效应,说明多种类型车队同时加载的情况都参与了超越率尾端分布的最终形成。而随着车道数的增加,加载的车辆数总体提高,车辆加载数少的情况对超越率尾部分布的贡献很小,可以近似忽略,所以最终总的超越率尾部分布实际是由多种类型(由同时加载的车辆数决定)的超越率分布叠加构成的。

图14 多车加载效应在超越数分布中的位置
由中心极限定理可知,当影响线内同时加载的车辆数较大时,任意时刻的荷载效应可认为近似服从正态分布,从而超越率分布近似符合Rice公式的函数形式,故交通比较密集时的超越率尾部分布近似由多个不同参数的Rice函数叠加而成(式(6)),并不符合Rice函数形式。这种分布形式一般对应长影响线,车道较多且交通处于高峰的情况。
(6)
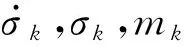
3) 极端稀疏情况
此种类型一般对应单车道短影响线或者交通处于低峰的情况。在交通特别稀疏的情况下,每次过桥基本都只有一辆车,效应峰值与车重基本成线性关系,且超越率分布形同效应随机过程峰值变量的累积分布。加上实际车重分布的尾端多服从正态或对数正态分布,所以最终的尾端超越率分布一般呈现仅正态叠加、仅对数正态叠加或者混合叠加的累积分布函数形式(式(7))。
(7)
式中,vxs(x)表示总效应超越率的尾部分布(正向效应为例);η表示车重与相应最大荷载效应的平均比值;f(w)表示车重分布;σj,μj表示对应j类车重分布的参数。
实际中,若各车道影响线差异较大,或者遇到影响线形状存在多个上升幅的情况,此公式的适用性将受到限制。
4) 其他情况
对于其他既不太密集也不太稀疏的交通情况而言,组成效应超越率分布的成分十分复杂,与车型组成、交通运行状态以及车重分布形式都有关系。其函数形式不固定,是否存在理论超越率分布难以直接判断,外推的潜在风险无法预计。
综上所述,Rice公式在实际效应超越率尾端分布中能够确定的适用范围极小,由此便会导致极限计算值出现较为显著的离散性问题,从而增大了效应外推的风险。
4 结 论
本文主要针对Cremona提出的基于Rice理论的极限值优化算法存在的计算结果离散性问题展开研究,并探究该问题产生的原因,结论如下:
(2) 分析样本本身的随机性也是导致计算结果离散性问题的重要原因,而效应外推方法又未对极限值的可靠性采取有效的评定措施,所以使用既有结果可能存在难以控制的风险。本文采用20组5年密集交通分别加载100 m简支跨中弯矩影响线外推计算不同重现期效应值。结果表明,根据具有相同车流特征和样本量的样本分析得到的极限效应值的变动范围较显著。其中,1年重现期效应值相差10.1%,1000年对应值相差22.5%。
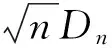
(4) 本文根据影响线范围内交通流的密集程度按极端密集、比较密集、极端稀疏以及其他情况共4种情况对效应超越界限率的尾端理论分布进行了讨论。结论认为,Rice公式在实际效应超越率分布中能够确定的适用范围极小,由此将导致较显著的极限计算值离散性问题。仅在本文的算例中,最优阀值的差别就超过124%,由此导致的2000年重现期效应计算值差别超过12%。
综上所述,若在实际操作中仍需采用基于Rice理论的算法分析极限效应,那么本文建议仅分析多车道大跨桥梁的荷载效应,且采用本文改进的阀值确定方式选取效应起点,并利用数值模拟技术增加计算次数,取结果的最大值作为极限估计值,以降低外推风险。
[ 1 ] Flint A R, Jacob B A. Extreme traffic loads on road bridges and target values for their effectsfor code calibration[C]. Proceedings of IABSE Colloquium-IABSE-AIPC-IVBH. Delft, the Netherlands, 1996: 469-478.
[ 2 ] O′Connor A, O′Brien E. Characteristic load effect prediction[M]. Vehicle-Infrastructure Interaction Ⅳ. Zakopane, Poland, 1999.
[ 3 ] Calgaro J A. Loads on bridges[J]. Progress in Structural Engineering and Materials, 1998, 1(4): 452-461.
[ 4 ] 阮欣, 周小燚, 郭济. 基于合成车流的桥梁车辆荷载效应极值预测[J]. 同济大学学报(自然科学版), 2012, 40(10): 1458-1485.
Ruan Xin, Zhou Xiaoyi, Guo Ji. Extreme value extrapolation for bridge vehichle load effect based on synthetic vehicle flow[J]. Journal of Tongji University (Natural Science), 2012, 40(10): 1458-1485. (in Chinese)
[ 5 ] Cremona C. Optimal extrapolation of traffic load effects[J]. Structural Safety, 2001, 23(1): 31-46.
[ 6 ] Cremona C. Probabilistic approach for cable residual strength assessment[J]. Engineering Structures, 2003, 25(3): 377-384.
[ 7 ] Cremona C, Carracilli J. Evaluation of extreme traffic load effects in cable stayed and suspension bridges using WIM records[C]. Proceedings of the 2nd European Conference on Weight-In-Motion of Road Vehicles. Lisbon, Portugal, 1998. 243-251.
[ 8 ] Rice S O. Mathematical analysis of random noise[J]. Bell System Technical Journal, 1944, 23(3): 282-332.
[ 9 ] Rice S O. Mathematical analysis of random noise[J]. Bell System Technical Journal, 1945, 24(1): 52-162.
[10] Getachew A. Traffic load effects on bridges: statistical analysis of collected and Monte Carlo simulated vehicle data[D]. SE-100 44 Stockholm, Sweden: Structural Engineering, Royal Institute of Technology, 2003.
[11] O′Connor A, O′Brien E J. Traffic load modelling and factors influencing the accuracy of predicted extremes[J]. Canadian Journal of Civil Engineering, 2005, 32(1): 270-278.
[12] 元宇,金红亮.Rice公式外推桥梁荷载效应[J].上海公路,2012,1:36-40.
Yuan Yu, Jin Hongliang. Extrapolation of load effect by rice fomula for bridges[J]. Shanghai Highways, 2012, 1: 36-40. (in Chinese)
[13] 应天益.基于WIM数据的桥梁汽车荷载及其效应分析[D]. 上海: 同济大学, 2009.
Yi Tianying. Analysis of vehicular load and its effect for bridges on the basis of WIM data [D]. Shanghai: Tongji University, 2009. (in Chinese)
[14] 金红亮. 桥梁评定极限荷载模型研究[D]. 上海: 同济大学, 2011.
Jin Hongliang. Study on the extreme load model for bridge assessment[D]. Shanghai: Tongji University, 2011. (in Chinese)
[15] 冯电视. 基于动态称重的桥梁运营荷载状况研究[D]. 上海: 同济大学, 2011.
Feng Dianshi. Study on the traffic load status of bridge in service on the basis of WIM data[D]. Shanghai: Tongji University, 2011. (in Chinese)
[16] 李扬海,鲍卫刚,郭修武,等. 公路桥梁结构可靠度与概率极限状态设计[M].北京:人民交通出版社,1997.
Li Yanghai, Bao Weigang, Guo Xiuwu, et al. Design of structural reliability and the probability limit state of highway bridge[M]. Beijing: China Communications Press, 1997. (in Chinese)
[17] Kolmogorov A. Sulla determinazione empirica di una legge di distribuzione[J]. Giornale dell′Istituto Italiano degli Attuari, 1933, 4: 83-91.
Dispersion Analysis of the Extreme Traffic Load Extrapolation and its Causes
YAN Bochong*
(Shanghai Donghua Local Railway Development Co., Ltd., Shanghai 200071, China)
China has witnessed quite a lot of structural damages and even collapses of highway bridges due to the increasing traffic loads; thus safety assessment is of great importance for structures in service. Many extreme load effect extrapolation, many researchers adopted the Rice′s formula to calculate the crossing level with an optimal threshold selection method proposed by Cremona. In this paper, the dispersion of the extreme load effect extrapolation and its cause were studied. Although the factors including subjectivity, sample randomness, and sample size contribute to the dispersion, it was concluded that the improper usage of K-S test and the improper hypothesis of level crossing rate distribution more affect the unreliable extrapolation.
highway bridge, traffic load, extreme effect, extrapolation dispersion
2014-01-28
*联系作者,Email: bochongyan@163.com

