混凝土-环氧树脂粘结界面的断裂模拟
陆洲导 姚晓璐 张远淼
(同济大学结构工程与防灾研究所,上海 200092)
混凝土-环氧树脂粘结界面的断裂模拟
陆洲导 姚晓璐*张远淼
(同济大学结构工程与防灾研究所,上海 200092)
在混凝土加固工程中,常采用环氧树脂等混凝土灌浆材料进行混凝土裂缝修复,会形成混凝土与环氧树脂的粘结界面。界面的强度影响结合材料强度,对界面性能的研究至关重要。基于ABAQUS采用内聚力单元和扩展有限元单元分别模拟界面断裂与混凝土断裂,以此研究含界面的混凝土断裂问题。讨论了界面粘结强度、混凝土抗拉强度、混凝土断裂能对含界面的楔入劈拉试件受力性能的影响。模拟结果表明,不仅数值分析结果与实验结果吻合较好,而且还能表现界面的损伤、断裂破坏过程,能够预测构件的承载力,有助于界面的优化设计。
楔入劈拉法, 内聚力单元, 扩展有限元, 粘结界面, 数值模拟
1 引 言
在混凝土修复与加固工程中,极易在混凝土与修复材料之间形成粘结界面,该粘结界面易发生脱粘破坏,影响其强度的发挥。含界面的混凝土断裂破坏主要有两种形式:①混凝土基体开裂;②界面破坏,包括修复材料的破坏。因其断裂破坏形式受界面性能和混凝土性能的影响,这种由界面到基体的开裂机制很难用单参数(能量判据)断裂力学方法解释[1]。
目前分离裂缝模型广泛应用于混凝土开裂的模拟分析。作为分离式裂缝模型的重要发展,Hillerborg等[2]于1976年提出了虚拟裂缝模型,并在混凝土和岩石等准脆性材料的开裂模拟方面得到了广泛的应用,取得了丰富的研究成果。
传统的虚拟裂缝模型中,裂缝两侧面之间只考虑沿其法向的分量的相互作用,仅考虑发生损伤微裂缝材料的剩余抗拉承载力对裂缝张开和扩展的影响。因此只适用于I型裂缝的模拟。但在实际材料的开裂过程中,裂缝两个侧面之间存在一定的抗剪切能力。基于此,对经典的虚拟裂缝力学模型进行了修正,引入沿缝面上的剪切变形影响。此类改进的虚拟裂缝模型被称为内聚力裂缝模型[3-5]。
内聚力裂缝模型模拟裂纹扩展是在裂纹可能的扩展路径上布置内聚力单元(cohesive element),其断裂过程用粘结法则来描述[3]。
但是由于内聚力裂缝模型模拟裂纹只能沿着单元边界扩展,因此往往伴随着网格的重划分,网格重划分不仅工作量大,还存在着新旧网格状态变量的映射等问题,导致运算效率降低,计算成本较高。在处理多裂纹问题时,特别是在开裂路径难以预知的情况下,使问题变得更加复杂[6]。
针对有限单元法处理裂纹等非连续界面问题存在的弊端,以美国西北大学Belytschko教授为代表的研究组1999年首先提出的扩展有限元法[7](eXtended Finite Element Method,XFEM)是近年来发展起来的求解不连续力学问题的一种有效数值方法。扩展有限元的核心思想是用扩充的带有不连续性质的形函数基来代表计算域内的间断,因此在计算过程中,不连续场的描述完全独立于网格边界,这使其在处理断裂问题上具有优势。扩展有限元中使用的网格与结构内部的几何或物理界面无关,从而克服了诸如裂纹尖端等高应力和变形集中区进行高密度网格剖分所带来的困难,模拟裂纹生长时也无须对网格进行重新剖分。而将扩展有限元方法和内聚力裂缝模型相结合,不仅继承了有限元的优点和技术,同时克服了内聚力单元对网格划分要求非常高的不足[1],因而受到了国内外众多学者们的关注,短短几年间就得到了快速的发展并获得了大量成果[8-10]。
本文采用内聚力裂缝模型和扩展有限元方法对不含界面的混凝土楔入劈拉试件的Ⅰ型断裂模拟,进一步分析不同的混凝土抗拉强度及不同的混凝土断裂能对裂纹扩展路径和荷载(P)-裂缝开口处张开位移(P-CMOD)曲线的影响,并与文献中的试验结果进行对比。随后利用cohesive element和XFEM各自的特点,采用cohesive element模拟粘结界面,采用XFEM模拟修复材料及被修复材料的裂缝扩展,来模拟含界面的楔入劈拉试件的I型断裂。进而研究界面粘结强度、混凝土抗拉强度、混凝土断裂能对含界面的楔入劈拉试件受力性能的影响。
2 损伤演化准则及起裂准则
在内聚力裂缝模型中裂纹面的应力-相对位移演化关系如下:
法向黏聚力σ仅与法向张开度δ有关,当δ>0且裂纹处于扩展状态时,σ不会立即降为零,而是随着裂纹的张开度δ的增加而逐渐减小,表现出软化特性。当δ>0但裂纹处于卸载或重新加载状态时,σ与δ保持线弹性关系,其刚度为初始刚度K0和损伤因子D的函数;当δ<0时,裂纹面发生相互嵌入,此时在裂纹面上设置法向弹簧以抵抗这种嵌入,弹簧刚度kn宜取较大值以控制嵌入量,如图1所示[11]。可以注意到ABAQUS中的黏聚力关系在应力上升段是非耦合的黏聚力关系,即计算某向应力随着位移的变化时不考虑其他方向上的位移对该向应力的影响[12]。
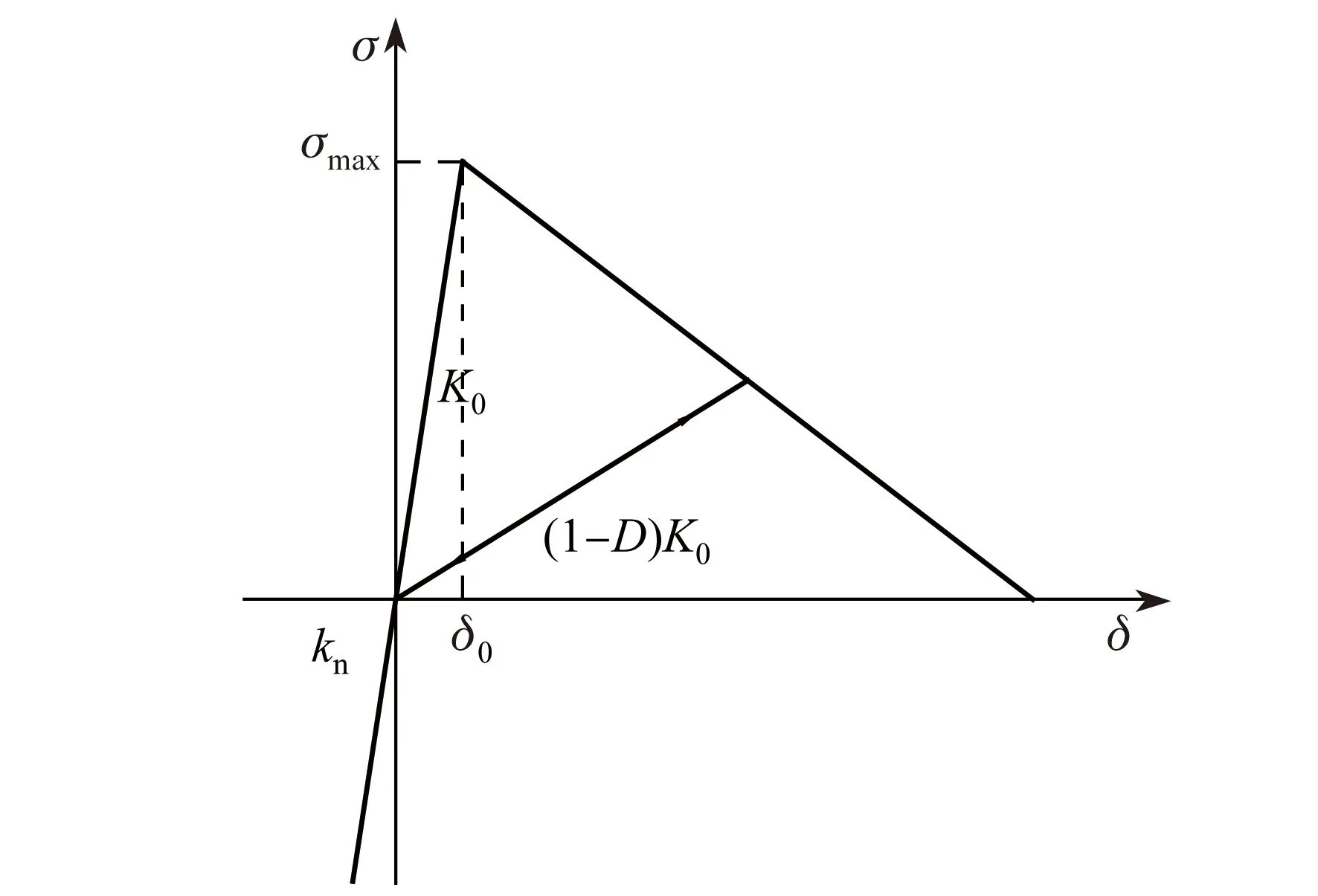
图1 黏聚裂纹本构关系
损伤采用损伤因子D来表示,D=0表示没有损伤,D=1表示完全损伤。
ABAQUS中对于内聚力单元设置了四种形式的单元初始损伤判据,用以计算在复合条件下单元的初始损伤条件,本文模型中采用了二次应力准则。
(1)
扩展有限元中,复合裂纹的起裂判据主要有最大切向应力、最小应变能密度因子和最大能量释放率三种准则。本文采用单元平均应力来作为起裂判据:①当单元平均应力的最大主应力达到材料的抗拉强度时,该单元裂纹开始产生;②裂纹开展方向与最大主应力方向垂直。上述判据可以作为最大切向应力准则的简化[11]。
3 混凝土楔入劈拉试验
本文主要模拟同济大学张远淼等所做过的含界面的楔入劈拉试验[13],试件的混凝土强度等级均按C30设计,试件尺寸为200 mm×200 mm×200 mm,采用细石混凝土。细石混凝土的配合比为水泥∶沙子∶细石∶水=1∶1.55∶3.61∶0.51。水泥为425#普通硅酸盐水泥,检验合格,沙子为细沙,细石最大粒径为10 mm,水是普通自来水。测得其立方体抗压强度为43.2 MPa。预制裂缝缝高均为50 mm。所采用的环氧树脂材料为XH160A/B环氧树脂胶裂缝修补胶及XH111NormalAB封闭胶[14]。该实验首先对混凝土楔入劈拉试件进行初次楔入劈拉试验,测得荷载及相关断裂参数(断裂韧度、断裂能),然后采用环氧树脂胶进行注胶修复,形成夹心楔入劈拉试件,对修复后的试件进行第二次楔入劈拉试验,通过比较注胶修复前、后试件的断裂韧度及断裂能、破坏模式,以此来分析环氧树脂与混凝土粘结界面的断裂性能。试验示意图如图2所示。为保证试验得到稳定的P-CMOD曲线,竖直荷载的施加采用荷载和位移双重控制。在控制作用力加载阶段,以30 N/s的速率进行加载直至2 kN;在控制位移加载阶段,以0.15 mm/min的速率加载直至试件破坏。

图2 原试件和夹心楔入劈拉试件示意图
4 楔入劈拉试验模拟
4.1 混凝土楔入劈拉试验模拟
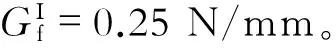
采用XFEM进行计算时,单元起裂采用最大切向应力准则,单元最大主应力达到混凝土抗拉强度ft=2.9 MPa时,单元起裂,同样采用基于能量的损伤演化准则。楔入劈拉试件模型如图3所示。

图3 楔入劈拉试件模型
采用cohesive单元与XFEM模拟混凝土开裂的模拟结果与试验结果对比如图4所示。可以发现,模拟结果与试验结果在试件初始刚度和极限承载力上吻合较好。

图4 楔入劈拉试验的模拟结果与试验结果
经过内聚力单元方法和扩展有限元方法的计算获得的P-CMOD曲线和实验中获得的P-CMOD曲线的对比,发现两种方法的计算结果和实验结果基本吻合。证明了内聚力模型和扩展有限元模型模拟楔入劈拉试件的I型断裂的适用性。
通过引用界面上的路径,可以比较界面上应力在不同时刻下的变化规律。图5、图6为开裂界面上的应力分析,横坐标为单元位置,即到预制裂缝的距离,纵坐标为应力大小。为了使计算过程更好地收敛,在计算时每个计算步的增量荷载不同,故两种方法总体计算步数不同。从曲线可以看出:①两种模拟方法得到的曲线整体趋势相同,cohesive单元的收敛性更好;②在加载初期,距预制裂缝较近的点受拉且应力较大,距预制裂缝较远的点受压且距离越远压应力越大;③随着继续加载,距离预制裂缝较近的点由于开裂逐渐退出工作(应力逐渐降为0),较远点开始受拉,直至整体受拉破坏;即开裂面上的应力随加载的进行,最大应力逐渐下移,开裂单元的应力也逐步衰减。采用内聚力单元与采用扩展有限元法计算的开裂面上的应力变化与分布规律相同。

图5 内聚力单元上节点的应力分布
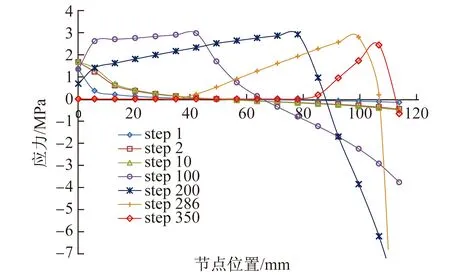
图6 XFEM开裂面上节点的应力分布
4.2 有界面试件模拟

图7为不同工况下的裂缝开裂模式。当混凝土抗拉强度小于界面单元的抗拉强度时,由于混凝土较为薄弱,裂缝在混凝土中发展,如图8(a)所示;当混凝土抗拉强度等于界面单元的抗拉强度时,混凝土与cohesive单元同时开裂,随后裂缝在界面开展;当混凝土抗拉强度大于界面单元的抗拉强度时,此时界面单元较为薄弱,裂缝在cohesive单元发展,如图8(b)所示。

图7 不同破坏模式
相对应于裂缝的开展模式,混凝土抗拉强度的不同取值决定了试件的P-CMOD曲线。图8为不同混凝土抗拉强度的模拟结果。当混凝土抗拉强度小于界面单元的抗拉强度时(ft 为了考察混凝土断裂能对试件受力性能的影响,分两种情况进行分析: (1) 混凝土抗拉强度为ft=2.0 MPa,小于界面单元抗拉强度值时,考察混凝土的断裂能取值Gf=0.10,0.25,0.35 N/mm时对P-CMOD曲线的影响; (2) 混凝土抗拉强度ft=3.5 MPa,大于界面单元抗拉强度值时,考察混凝土的断裂能取值Gf=0.10,0.25,0.35 N/mm时对P-CMOD曲线的影响。 从混凝土不同断裂能的模拟结果来看,当fb>ft时,由于混凝土比界面弱,损伤集中于混凝土,构件极限承载力峰值和延性会随混凝土的断裂能的增加而增加,与文献[15]的结论相同。采用不同的软化曲线对P-CMOD曲线是有较大影响的,初始断裂能Gf和抗拉强度ft对极限荷载影响较大,总断裂能对曲线的尾部影响大,如图9所示。当fb≤ft时,由于界面比混凝土弱,损伤集中于界面,因而当界面出现破坏时,改变混凝土的断裂能对P-CMOD曲线影响甚微,如图10所示。 (1) 通过采用cohesive单元与XFEM模拟混凝土开裂的模拟结果与试验结果的对比,可以发现,模拟结果与试验结果吻合较好。充分证明目前广泛采用的内聚力单元和扩展有限元方法模拟混凝土楔入劈拉试件I型断裂具有很好的适用性。 图9 不同断裂能的模拟结果(混凝土抗拉强度ft=2.0 MPa) 图10 不同断裂能的模拟结果(混凝土抗拉强度ft=3.5 MPa) (2) 通过采用cohesive单元与XFEM模拟混凝土开裂的模拟计算步数的对比,可以发现Cohesive单元的收敛性更好。 (3) 通过采用cohesive单元模拟粘结界面,而采用XFEM模拟修复材料及被修复材料的裂缝扩展,比较不同混凝土抗拉强度下P-CMOD曲线,当fb>ft时,由于混凝土比界面弱,损伤集中于混凝土,构件极限承载力和峰后延性会随混凝土的断裂能的增加而增加,与文献[15]的结论相同。采用不同的软化曲线对P-CMOD曲线是有较大影响的,初始断裂能Gf和抗拉强度ft对极限荷载影响较大,总断裂能对曲线的尾部影响大。当fb≤ft时,由于界面比混凝土弱,损伤集中于界面,因而当界面出现破坏时,改变混凝土的断裂能对P-CMOD曲线影响甚微,有助于优化界面设计以及对提升加固体系的整体性有参考意义。 [ 1 ] 陈瑛,乔丕忠,姜弘道,等.FRP-混凝土三点受弯梁损伤粘结模型有限元分析[J].工程力学,2008,25(3):120-125,131. Chen Ying, Qiao Pizhong, Jiang Hongdao, et al. Numerical modeling for cohesive fracture of FRP-concrete bonded interfaces in three-point bend beams.[J]. Engineering Mechanics, 2008,25(3): 120-125, 131. (in Chinese) [ 2 ] Hillerborg A, Modéer M, Petersson P E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements[J]. Cement and Concrete Research, 1976, 6(6): 773-781. [ 3 ] Barenblatt G I. The mathematical theory of equilibrium cracks in brittle fracture [J]. Advances in Applied Mechanics, 1962, 7: 55-129. [ 4 ] Dugdale D S. Yielding of steel sheets containing slits [J]. Journal of Mechanics and Physics of Solids, 1960, 8:100-108. [ 5 ] Hillerborg A. Results of three comparative test series for determining the fracture energy GF of concrete [J]. Materials and Structures, 1985, 18: 407-413. [ 6 ] 李录贤,王铁军.扩展有限元法(XFEM)及其应用[J].力学进展,2005,35(1): 5-20. Li Luxian, Wang Tiejun. The extended finite element method and its applications-A review [J]. Advances in mechanics, 2005,35(1): 5-20. (in Chinese) [ 7 ] Belytschko T, Black T. Elastic crack growth in finite elements with minimal remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 45(5): 601-620. [ 8 ] Stolarska M, Chopp D L, Mo⊇s N, et al. Modelling crack growth by level sets in the extended finite element method[J]. International Journal for Numerical Methods in Engineering, 2001, 51(8): 943-960. [ 9 ] Nagashima T, Omoto Y, Tani S. Stress intensity factor analysis of interface cracks using X-FEM[J]. International Journal for Numerical Methods in Engineering, 2003, 56(8): 1151-1173. [10] Dolbow J, Mo⊇s N, Belytschko T. An extended finite element method for modeling crack growth with frictional contact[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190(51): 6825-6846. [11] 方修君,金峰,王进廷.用扩展有限元方法模拟混凝土的复合型开裂过程 [J]. 工程力学,2007, 24(1): 46-52. Fang Xiujun, Jin Feng, Wang Jinting. Simulation of mixed-mode fracture of concrete using extended finite element method[J]. Engineering Mechanics, 2007, 24(1): 46-52. (in Chinese) [12] 张军.界面应力及内聚力模型在界面力学的应用[M].郑州:郑州大学出版社,2011. Zhang jun. Interfacial stress and cohesive zone model in the interface mechanics [M]. Zhengzhou: Zhengzhou University Press, 2011. (in Chinese) [13] 张远淼,余江滔,陆洲导.混凝土-环氧树脂黏结界面的断裂性能分析[J].同济大学学报,2014,42(07):1031-1037. Zhang Yuanmiao, Yu Jiangtao, Lu Zhoudao. Analysis on fracture properties of concrete-epoxy interface[J]. Journal of Tongji University, 2014, 42(07): 1031-1037. (in Chinese) [14] 张辉,余江滔,张远淼,等.混凝土与环氧树脂粘结界面断裂性能试验研究[J]. 结构工程师,2014,30(02):127-132. Zhang Hui, Yu Jiangtao, Zhang Yuanmiao, et al. Fracture experimental study of the bonding interface between concrete and epoxy resin [J]. Structural Engineers, 2014, 30(02): 127-132. (in Chinese) [15] Park K, Paulino G H, Roesler J R. Determination of the kink point in the bilinear softening model for concrete[J]. Engineering Fracture Mechanics, 2008, 75(13): 3806-3818. Fracture Simulation of Concrete-epoxy Bonding Interface LU Zhoudao YAO Xiaolu*ZHANG Yuanmiao (Research Institute of Structural Engineering and Disaster Reduction, Tongji University, Shanghai 200092, China) Concrete grouting materials such as epoxy resin are more and more widely used to repair concrete cracks. A bonding interface between the epoxy resin and concrete or between new and old concrete is formed. The bond strength of the interface is the main factor affecting the strength of the composite materials. Therefore, the study of the interfacial properties is very important. This paper adopted the cohesive element and the extended finite element in ABAQUS to simulate interface fracture and concrete fracture. The influence of the cohesive strength of interface, the concrete tensile strength and the fracture energy on the wedge splitting specimen performance were discussed in detail. The results presented in this study are helpful for studying interface fracture process, predicting the load-carrying capacity and ductility, and optimizing the interface design. wedge splitting test, cohesive element, extended finite element, concrete-epoxy interface, concrete fracture simulation 2013-12-19 国家自然科学基金(51008235,51378397) *联系作者,Email: yaoxiaolu1201@126.com

5 结 论



