挖掘隐含图形条件，强化数形结合思想——以“圆”为例

马玉红（江苏省昆山震川高级中学215300）

挖掘隐含图形条件，强化数形结合思想
——以“圆”为例

马玉红（江苏省昆山震川高级中学215300）

一、问题的提出

聚焦高考，历年来解析几何都是高考考查的重要内容，因此，也是高考命题的重点、热点。客观题以中、低档题为主，主观题以中、高档题为主，难度较大。一般学生都感觉计算量大且复杂，费时费力却不易得出结果。

究其原因，解析几何是建立在坐标系的基础上，用坐标表示点，用方程表示曲线，通过代数运算处理几何问题的一门学科。基本思想就是通过坐标将几何图形转化为方程，通过对方程的研究达到研究几何图形性质的目的，坐标法将形与数统一起来，从而达到定性定量的研究。但是一味强调解析几何中的定量计算，有时会导致大量的繁琐解题过程，学生在进行大量的计算以后而得不出结果。如果在进行计算的同时恰当地应用平面几何的一些相关知识，则可以往往产生一些意想不到的效果。

如2013年江苏高考数学第17题第（2）问：在平面直角坐标系xOy中，点A（0,3），直线I：y=2x-4。设圆的半径为1，圆心在l上。若圆C上存在点M，使MA=2MO，求圆心C的横坐标a的取值范围。

本题第（2）问中，如果先利用几何条件MA=2MO得出点M的轨迹是圆P，由题意得同时点M在圆C上，则问题转化为圆与圆有公共点，即转化为为两圆的位置关系，利用圆心距和半径列出不等式就可求出答案。而部分学生设P点利用方程组恒有解，则计算繁难，不易得出结果。

这道题在用解析几何方法解题时，如果充分结合圆的有关几何知识则问题马上解决，且计算比较简单。

本文试着探索平面几何与解析几何之间的依存关系。如何将两种几何存在的客观事实由几何问题向代数问题转化，实现形与数的高度统一，又结合几何性质约束简化代数计算问题，以“圆”为例加以分析说明。

二、具体的做法

（一）抓住变形方程代表特定曲线挖掘几何图形

解析几何主要运用代数方法解决几何问题，反之，如代数问题解决困难时，也可以用几何问题处理。如：若直线y=x+b与曲线y=3-有公共点，则b的取值范围为____。本题若用代数方法处理在 x∈[0,4]有解的话，需要分类讨论，运算量较大，不易解出正确答案。如细心观察，善于挖掘，不难发现曲线是以（2，3）为圆心，2为半径的圆的下半圆，转化为直线与半圆有公共点问题，得到

（二）从题目蕴涵几何定义挖掘几何图形

几何定义是解析几何的基础，对学生来说尤为重要，但学生在学习时不善于把握定义，不能准确给出定义，做题目时就发现不了几何图形。如：若圆（x-2）2+y2=1上存在两个点P，O,它们到直线y=kx+1的距离都等于1，则实数k的取值范围为____。如对平面几何知识掌握的比较好，善于发现，会得到到直线距离等于1的点，在与这条直线距离为1的两条平行线上，题目转化为两直线与圆有两个公共点问题。如：若与点A（2,2）距离为1，且与点B（m，0）距离为3的直线恰有两条，则m的取值范围是____。本题结合圆的定义，借助两圆公切线问题转化为两圆的位置关系，用圆心距和半径比较，图形语言向代数语言转化即可得到结果。如：已知圆C：（x-a）2+（ya）2=9，在圆C上总存在两点到原点的距离等于1，则实数a的取值范围是____。如能发现到原点的距离等于1的轨迹是以原点为圆心，1为半径的圆O，题目就转化为圆O与圆C相交，列出就能得到答案.如果采用代数方法利用方程有解很繁，且不容易得出结果。

（三）从图形中挖掘满足几何性质的几何图形

解析几何虽然提倡用代数方法解题，但属于几何范畴，如把握好几何图形及性质，数形结合，会更有效解决问题。

如：定理：已知圆C中弦AB的中点为M，则CM垂直平分AB即CM⊥AB,AM=BM利用该定理，构造直角三角形，可以解决一类轨迹方程问题，减少大量的代数计算。

如：已知圆C：x2+y2=a2，点A为圆内任一点，过点A作互相垂直的两条射线分别交圆C于P，Q,以AP,AQ为边作矩形APDQ，则点D的轨迹是什么？

此题可设AC=b，作CE⊥DP交DP于E，AQ于F，作CG⊥AP令＜CAQ=a，则CF=bsina,

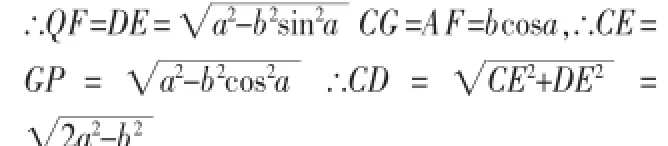
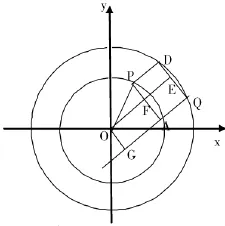
应用1：已知圆O：x2+y2=16内的一点M（1,2）过M作互相垂直的两条射线分别交圆于P，O,两点，且的范围。

如图，已知小圆半径为R1，大圆半径为R2，过定点A作互相垂直的两条射线分别交小圆，大圆于P，Q两点，则矩形APDQ的顶点D的轨迹是以O为圆心，半径为的圆。

应用2：已知两圆x2+y2=4，x2+y2=16，M（1, 0），过点M作MP⊥MQ分别与两圆交于P，Q两点，求PQ的取值范围。由上述结论，得矩形MPDQ的顶点D的轨迹是以O为圆心，为半径的圆，即x2+y2=19，所以MD的范围是

解析几何虽然注重用代数方法处理几何问题，但过于繁杂也不是考查的要点，不能过于强调死算，处理解析几何的有关问题时，要善于挖掘图形中所隐含的几何因素，利用有关的平面几何知识使解题过程变得简洁优美。

（责编田彩霞）