粗粒料颗粒破碎数值模拟研究
杨 贵 ,许建宝 ,刘昆林
(1.河海大学 安全与防灾工程研究所,江苏 南京 210098;2.河海大学 岩土力学与堤坝工程教育部重点试验室,江苏 南京 210098)
1 引 言
堆石料作为典型的颗粒摩擦材料,具有显著的颗粒破碎特性,且随着堆石料颗粒尺寸的增大,颗粒破碎特征越明显。颗粒破碎使得堆石料体积收缩并成为影响面板坝应力、变形的决定性因素[1]。忽略颗粒破碎特性,将难以透彻理解和描述堆石料力学特性,是当前高土石坝本构模型中的研究热点。
颗粒破碎的机制非常复杂,众多学者从室内试验,数值模拟和理论分析等手段进行了广泛研究[2-6]。一般根据试验前后颗粒级配的变化进行颗粒破碎分析,忽略了试样制备和固结过程对颗粒破碎的影响。高玉峰等[3]研究结果表明,试样在制备过程中发生的颗粒破碎不可忽视,为了在固结开始前保持初始设计的级配,应将设计级配曲线相应下调6%来制备试样。对试样在剪切过程中颗粒破碎特征未能进行广泛研究,主要是由于受试验条件的限制。
颗粒流方法作为一种能够有效模拟粗粒料力学特性的方法,在岩土工程的众多领域得到广泛应用[7-9]。本文基于二维颗粒流程序,建立粗粒料颗粒破碎模型,开展堆石料双轴剪切试验数值模拟研究,分析粗粒料在剪切过程中颗粒破碎的变化特征。
2 考虑粗粒料颗粒破碎的数值模型
数值模拟过程中关于颗粒破碎的模拟,目前主要有两种方法:一种是采用组合颗粒来替代单一的模型颗粒,颗粒与颗粒之间通过接触粘结和并行粘结进行联系,在外力荷载作用下当颗粒之间的粘结力小于破碎力时,颗粒发生破碎[10];另一种是采用离散方法,即当颗粒的受力状态满足一定的破坏标准时颗粒发生破碎,采用按照一定形状排列组合的颗粒代替原来的颗粒[9,11]。
两种方法各有优缺点,前一种方法能够方便地模拟粗颗粒材料的形状,缺点是颗粒之间的粘结力确定比较复杂,在外力作用下,颗粒不能进行二次破碎,破碎后颗粒级配曲线很难获得,无法与实际试验结果进行对比验证,计算过程中因预先进行了颗粒替换,试样颗粒数目较多,计算效率较低。后一种方法的缺点在于不能模拟颗粒材料的复杂形状,其优点在于能够实现颗粒的二次破碎,只有当颗粒的应力达到其破坏标准时才发生破坏,试样颗粒数目较少,计算效率较高,能够方便地统计试验过程中颗粒级配,分析其变化规律并与室内试验结果进行对比。
单颗粒的破碎过程一般采用单向抗压试验和巴西圆盘劈裂试验来进行模拟。认为颗粒的破碎形式是拉裂破坏或剪切破坏。研究过程中,一般认为,颗粒的实际受力状态可以简化为静水压力和相互垂直的主应力作用,如图1 所示。
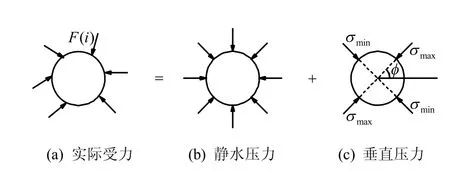
图1 颗粒受力简化图Fig.1 Schematic of particle stress state
部分学者认为,颗粒在静水压力作用下不会发生破坏,只有在主应力作用下才会发生破坏,且破坏形式为拉裂破坏[9]。在实际过程中,颗粒在外荷载作用下,周边接触颗粒的数目是有限的,不能完全等效为静水压力的作用,因此,有学者提出,颗粒在等向应力荷载作用下也会发生破坏,且破坏类型为剪切破坏[11]。
对于颗粒的拉破坏,采用Oliver 等[9]根据圆盘劈裂原理建立的拉破坏准则,即:
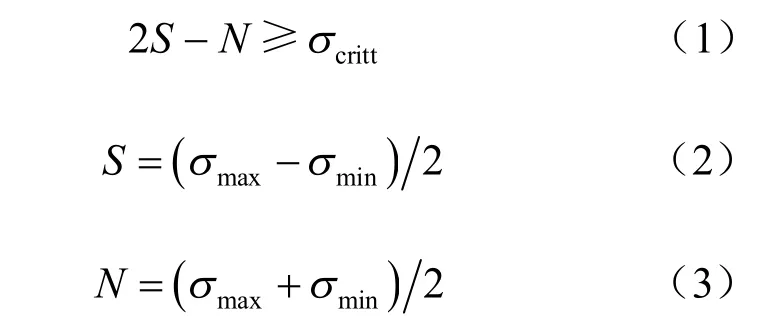
式中:σcritt为颗粒极限抗拉强度;σmax为颗粒最大主应力;σmin为颗粒最小主应力。
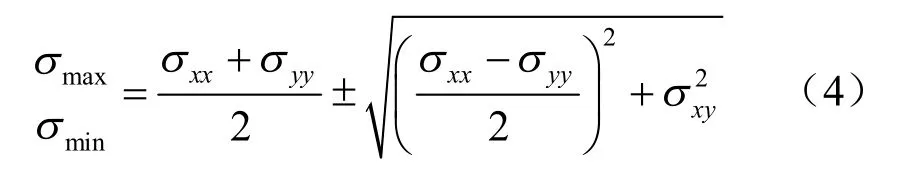
式中:σxx为颗粒x 向正应力;σyy为颗粒y 向正应力;σxy颗粒xy 方向的剪应力。
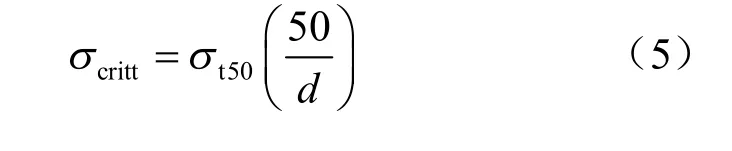
式中:σt50为直径为50 mm 颗粒的抗拉强度;d为颗粒直径(mm)。
对于压破碎的颗粒,当颗粒所受的应力状态满足下列公式时,则发生破坏。

式中:N为颗粒周边的接触数目;σi为颗粒周边某一接触的法向应力。
考虑到不同直径颗粒其抗压强度不同,结合Hoek 等对不同尺寸岩石试样的研究成果,以及Ben-Nun 等[11]数值模拟研究成果,定义颗粒的极限抗压强度 σcritc为
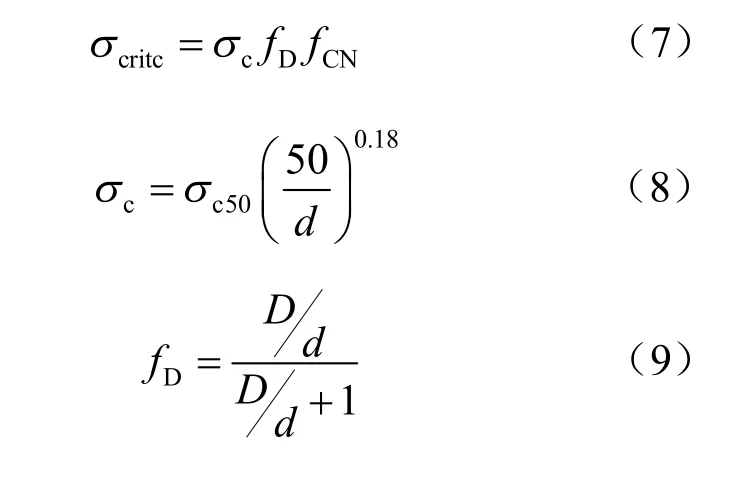
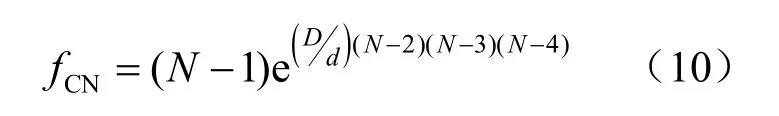
式中:σc为颗粒单轴抗压强度;fD为颗粒直径影响系数;fCD为颗粒接触影响系数;σc50为直径为50 mm 颗粒的单轴抗压强度;D为当前颗粒周边接触颗粒平均直径,当接触对象为墙体时,D为无穷大,此时 fD=1 ;d为颗粒直径;N为颗粒接触数目。
数值模拟过程中对颗粒所受的应力状态进行分析,当颗粒间的接触数目 <3 时,颗粒只发生拉破碎;当颗粒数目 ≥3 时,颗粒发生压破碎或拉破碎。当颗粒满足破碎强度准则时,采用如图2 所示的颗粒进行替换,替换后颗粒的材料属性与替换前一致。各颗粒的大小和位置关系如图2 所示。组合颗粒的主轴方向φ 根据原颗粒所受的最大压力方向确定。
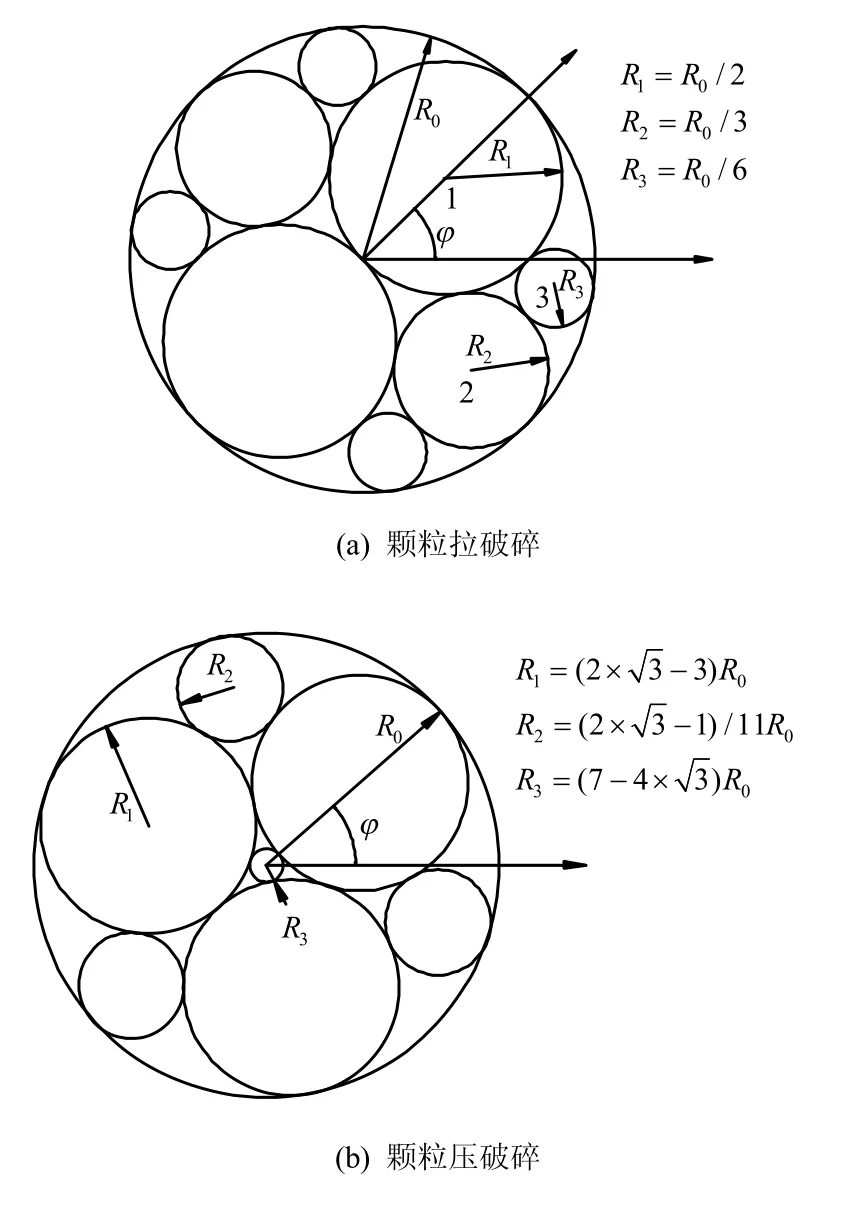
图2 单颗粒破碎组合关系Fig.2 Schematic of particle composition
从图2 可以看出,采用组合颗粒后,会导致部分面积缺少。为了弥补缺失的面积,部分学者采用了面积不变的原则,也叫膨胀法,即在生成替换颗粒的过程中,将颗粒的半径进行放大。本文采用增加新增颗粒密度的方法进行控制,即密度法,从而使得替换颗粒前后的总质量不变。
对于拉破碎情况,设原颗粒的密度为ρ,颗粒半径为R0,替换后的颗粒密度为ρ′,颗粒半径分别为R1、R2和R3,则有:
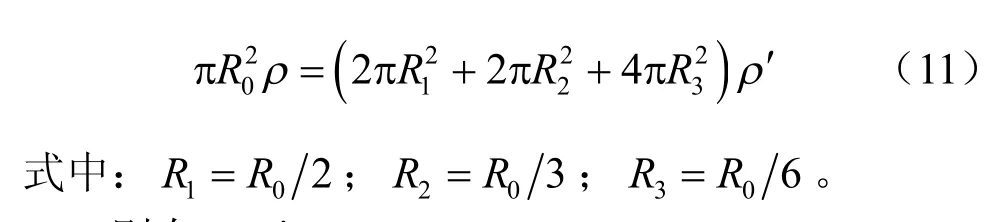
则有:ρ′=1.2ρ
压破碎的密度处理方法与拉破碎一致。考虑到实际工程中,当外荷载一定时,颗粒不能无限制破碎下去,且为了提高数值模拟的计算效率,定义最小不破碎颗粒直径dmin,当颗粒直径大于该值时才会发生破碎,否则不发生破碎。
3 数值模拟结果验证
为进行数值模型的验证,首先需要能够模拟真实的室内三轴试验成果。基于此,选取江苏宜兴抽水蓄能电站筑坝堆石料大型三轴剪切试验结果作为本次数值模拟的考题。试样干密度为2.12 g/cm3,相对密度为0.95,最大粒径为60 mm,不均匀系数为52.5,曲率系数为1.07。试验级配曲线如图3 所示,试样尺寸直径为300 mm,高度为600 mm。
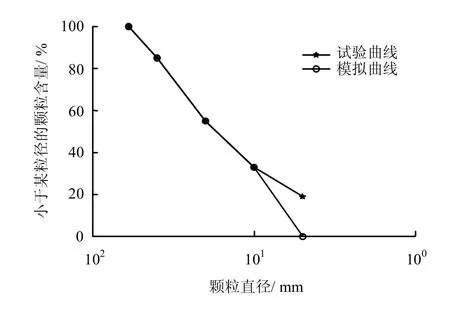
图3 试验和数值模拟级配曲线Fig.3 Testing and simulation gradation curves
数值模拟过程中,采用如图3 所示的试验级配进行模拟,为提高计算效率限制试样生成过程中最小颗粒直径,并将试样尺寸和试验级配同时放大10倍,生成后的试样颗粒总数为2 473,已有研究表明,当试样尺寸的直径和高度比保持不变,尺寸变化而带来的差异可以通过细观参数的变化来反映[12]。本文采用的颗粒接触模型为非线性H-Z 模型,细观参数如表1 所示。

表1 颗粒流数值模拟的参数Table 1 Parameters used in PFC2D simulation
表1为根据堆石料室内试验600 kPa 围压下的结果进行模型参数标定后的结果,图4为数值模拟结果与试验结果。在模型参数不变的条件下,开展了围压900 kPa 的三轴剪切试验模拟,结果如图4所示。
从图中可以看出,无论是轴向应力-应变曲线,还是体积应变-轴向应变曲线,数值模拟结果都能与试验结果吻合较好;因此,可以认为本文建立的粗粒料颗粒破碎数值模型和选取的模型参数能够较好地模拟室内试验开展的堆石料静力特性。
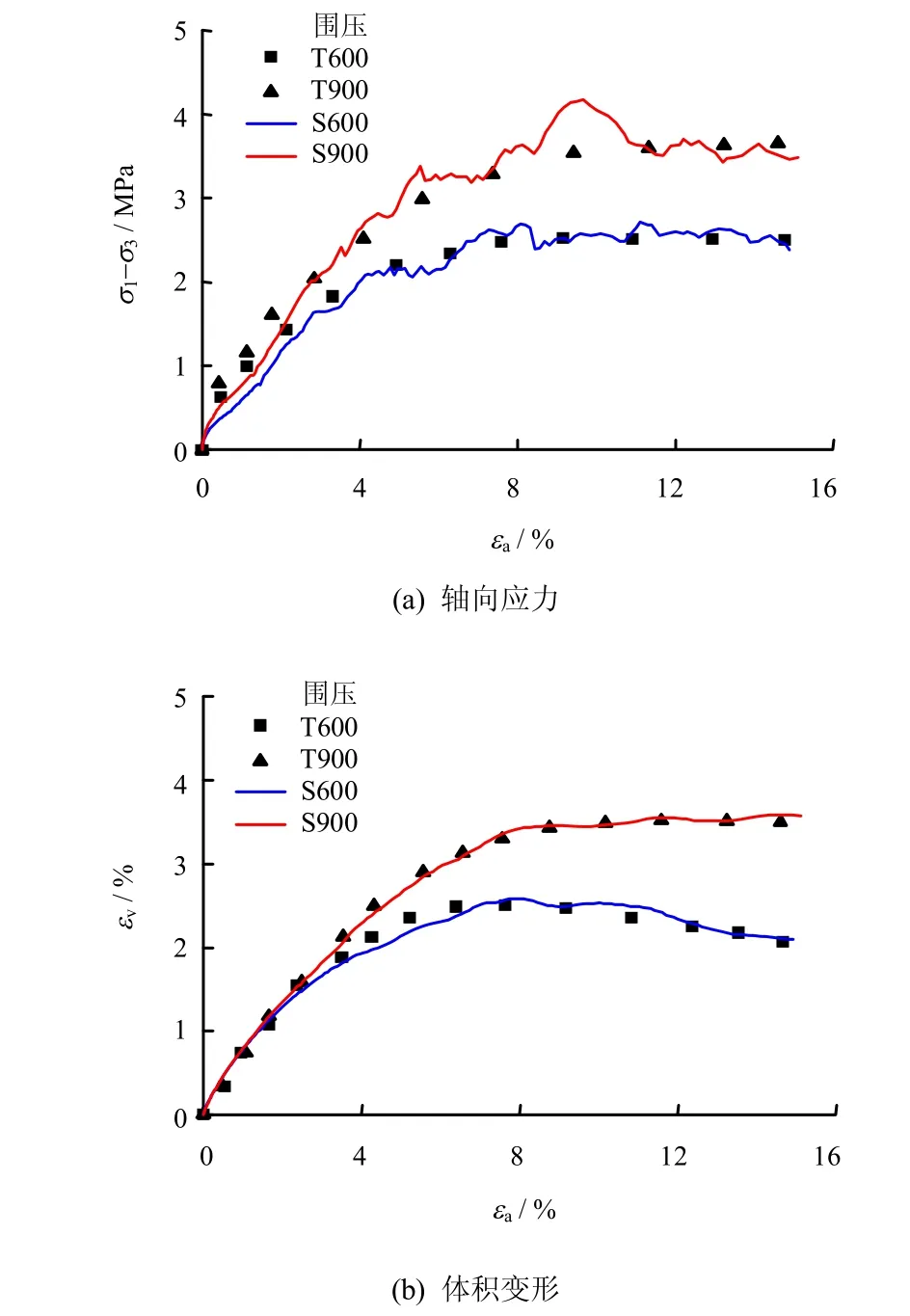
图4 堆石料三轴剪切试验结果Fig.4 Triaxial shear test results of rockfill material
4 数值模拟结果分析
4.1 围压影响分析
本文采用Marsal[13]提出的颗粒破碎指标Bg定量描述颗粒破碎的程度。
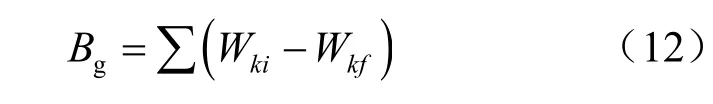
式中:Wki为试验开始前某级配粒组的含量;Wkf为试验后对应同一级配粒组的含量。
表2为数值模拟过程中,不同轴向应变时刻对应的颗粒破碎率。从表中可以看出,采用本文提出的方法在数值模拟过程中轴向应变为15%时刻的颗粒破碎率与试验结果基本一致,而采用膨胀法的数值模拟结果差异较大,结合不同围压下轴向应变、体积应变和轴向偏应力条件下的数值模拟结果与试验结果的对比情况,表明本文建立的细观数值模型基本能够反映堆石料的在荷载作用下的颗粒破碎特征。从表2 还可以看出,试样在制备和等向固结过程中存在明显的颗粒破碎特征,随着围压的增大,本次试验获得的颗粒破碎率变化不明显。不同围压下的试验制备和固结过程而引起的颗粒破碎均为1.13,约占整个破碎率的9.7%和8.1%。该结论与高玉峰等[3]的研究成果类似。其原因可能是由于试验初始孔隙率较小,相对密度较大,试验制备过程对颗粒破碎的影响明显优于试验围压对颗粒破碎的影响。
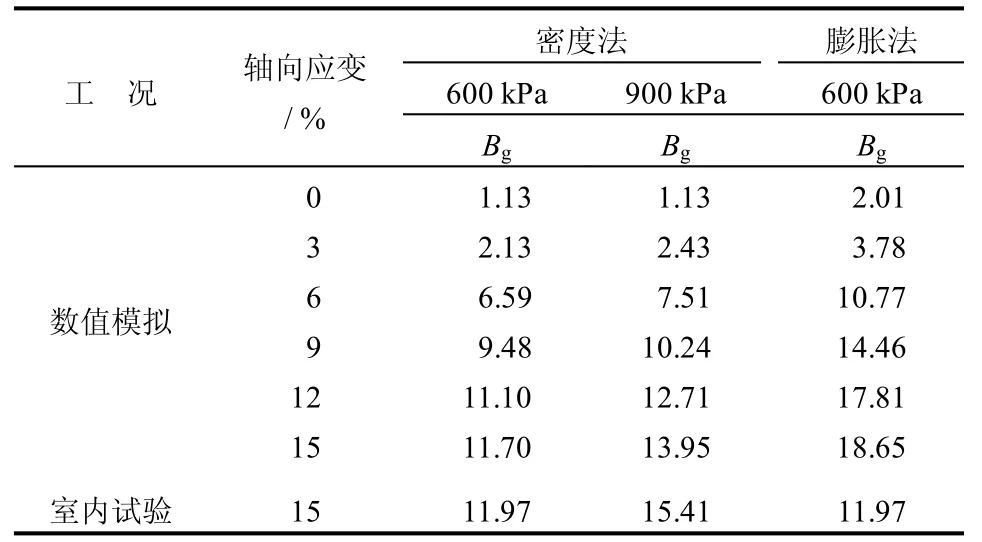
表2 堆石料试验和数值模拟颗粒破碎率Table 2 Testing and numerical simulation results of particle breakage rate of rockfill
随着轴向应变的增大,颗粒破碎逐渐增多,破碎率增大,近似呈非线性增长;当去除试样制备和固结过程引起的颗粒破碎,不同围压和不同模拟方法获得的颗粒破碎率归一化后具有较好的一致性(如图5 所示),可近似采用双曲线函数进行拟合。
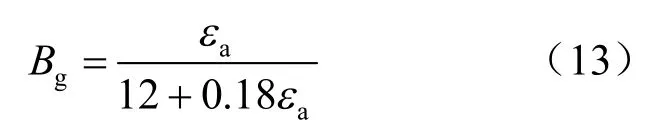
式中:εa为轴向应变。
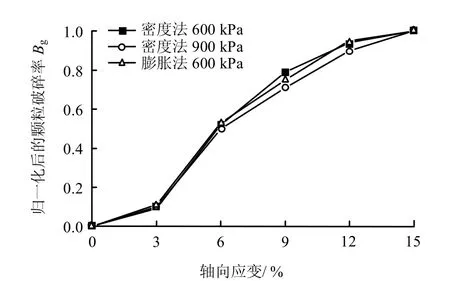
图5 归一化颗粒破碎与轴向应变关系Fig.5 Relationships between axial strain and normalized particle breakage
图6为不同围压条件下三轴剪切试验初始和最终级配曲线及根据Einav[14]基于分形理论提出的粗粒料颗粒破碎理论曲线,公式如下:
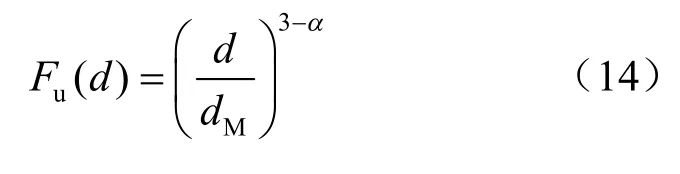
式中:dM为试样中的最大颗粒直径;d为颗粒直径;α为分形维数,对于多数材料设定为常数2.6。
从图6 可以看出,随着围压的增大不同级配条件下的试样最终的级配曲线趋于Einav[14]提出的颗粒破碎的最终级配(图中α=2.6)。表明,堆石料在颗粒破碎过程中存在一定的分形特征。
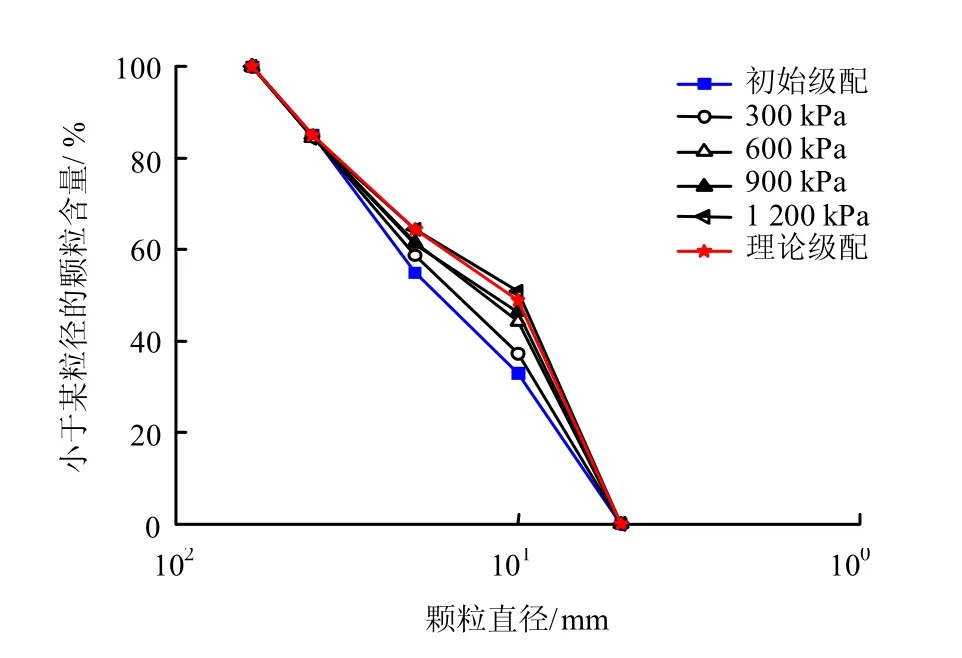
图6 不同围压下试验级配曲线Fig.6 Gradation curves under different confining pressures
4.2 数值模拟方法对比分析
数值模拟成功的关键在于建立合适的数值模型,不同的数值模型可能获得的试验规律是相反的,模型参数的选择对数值模拟结果影响较大,但规律基本不变。基于此,采用相同的细观数值模拟参数,分析了不同模拟方法对试验结果的影响。
图7为采用密度法和膨胀法两种分析方法获得的数值模拟结果。从图中可以看出,对于轴向应变与偏应力的关系,两种不同数值模拟方法的结果差异较小,与试验结果基本吻合(见图7(a))。但在轴向应变与体积应变方面,两者差异较大,采用膨胀法获得的结果存在明显的剪胀现象,见图7(b)。在轴向应变小于4%的情况下,两种不同数值模拟方法获得的数值模拟结果基本一致。在应变大于4%的情况下,两种不同数值模拟方法获得的数值模拟结果差异较大。对比颗粒破碎率可知,在低应变条件下颗粒破碎较小,因此,两种分析方法差别不大;随着轴向应变的增大,颗粒破碎越多,两种分析方法之间的差异逐渐显露出来。
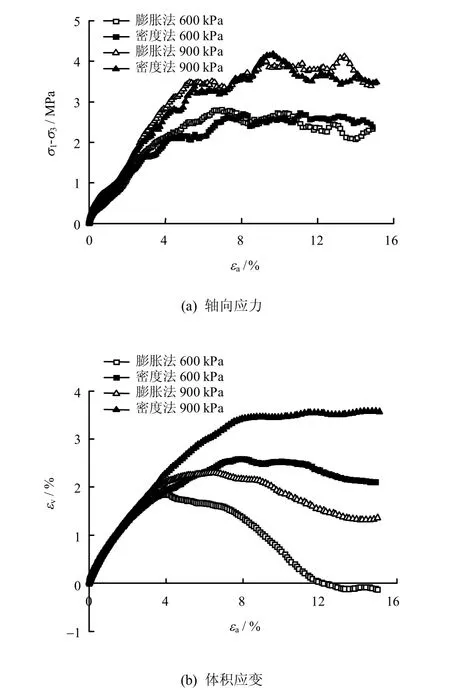
图7 不同模拟方法结果分析Fig.7 Results obtained by different simulation methods
5 结 论
(1)采用Hoek 等对不同尺寸岩石试样的研究成果和颗粒破碎过程中保持总质量不变,通过改变密度来实现,建立的数值模型能够近似反映粗粒料颗粒破碎特性。
(2)试验过程中,随着轴向应变的增大,颗粒破碎逐渐增多,去除试样制备和固结过程引起的颗粒破碎,不同围压条件下的颗粒破碎率归一化后基本重合,且可以近似采用双曲线函数进行拟合。
(3)颗粒破碎随着围压的增大,逐渐增大,试验级配趋于Einav 提出的颗粒破碎的最终级配。
[1]沈珠江.面板堆石坝应力应变分析的若干问题[C]//中国混凝土面板堆石坝十年学术研讨会论文集(1985-1995).北京:中国水利水电出版社,1995:43-50.SHEN Zhu-jiang.Problems of concrete faced rockfill dam stress and deformation analysis[C]//Proceedings of the 10th Chinese Academic Conference on Concrete Faced Rockfill Dam(1985-1995).Beijing:China Water &Power Press,1995:43-50.
[2]刘汉龙,秦红玉,高玉峰,等.堆石粗粒料颗粒破碎试验研究[J].岩土力学,2005,26(4):562-566.LIU Han-long,QIN Hong-yu,GAO Yu-feng,et al.Experimental study on particle breakage of rockfill and coarse aggregates[J].Rock and Soil Mechanics,2005,26(4):526-566.
[3]高玉峰,张兵,刘伟,等.堆石料颗粒破碎特征的大型三轴试验研究[J].岩土力学,2009,30(5):1237-1241.GAO Yu-feng,ZHANG Bing,LIU Wei,et al.Experimental study on particle breakage behavior of rockfills in large-scale triaxial tests[J].Rock and Soil Mechanics,2009 30(5):1237-1241.
[4]陈生水,傅中志,韩华强,等.一个考虑颗粒破碎的堆石料弹塑性本构模型[J].岩土工程学报,2011,(10):1489-1495.CHEN Sheng-shui,FU Zhong-zhi,HAN Hua-qiang,et al.An elastoplastic model for rockfill materials considering particle breakage[J].Chinese Journal of Geotechnical Engineering,2011,(10):1489-1495.
[5]BAGHERZADEH-KHALKHALL A,MOHAMMADI S.Numerical simulation of particle breakage of angular particles using combined DEM and FEM[J].Powder Technology,2011,20(11):15-29.
[6]BAGHERZADEH-KHALKHALL A,MOHAMMADI S.Micromechanics of breakage in sharp-edge particles using combined DEM and FEM[J].Particuology,2008,(6):347-361.
[7]杨贵,肖杨,高德清.粗粒料三维颗粒流数值模拟及其破坏准则研究[J].岩土力学,2010,31(增刊2):402-406.YANG Gui,XIAO Yang,GAO De-qing.Study ofthree-dimensional particle flow numerical simulation and failure criterion for coarse-grained soils[J].Rock and Soil Mechanics,2010,31(Supp.2):402-406.
[8]周健,王家全,曾远,等.颗粒流强度折减法和重力增加法的边坡安全系数研究[J].岩土力学,2009,30(6):1549-1554.ZHOU Jian,WANG Jia-quan,ZENG Yuan,et al.Slope safety factor by methods of particle flow code strength reduction and gravity increase[J].Rock and Soil Mechanics,2009,30(6):1549-1554.
[9]OLIVIER T D V,JEAN-CLAUDE C.Numerical model of crushing of grains inside two-dimensional granular materials[J].Powder Technology,1999,(105):190-198.
[10]刘君,刘福海,孔宪京.考虑破碎的堆石料颗粒流数值模拟[J].岩土力学,2008,29(增刊):107-112.LIU Jun,LIU Fu-hai,KONG Xian-jing.Particle flow code numerical simulation of particle breakage of rockfill[J].Rock and Soil Mechanics,2008,29(Supp.):107-102.
[11]BEN-NUM O,EINAV I.The role of self-organization during confined comminution of granular materials[J].Philosophical Transactions of the Royal Society A,2010,36(8):231-247.
[12]YANG G,LIU K L,LIU H L.Dynamic deformation behaviour of coarse aggregate under cyclic loading by PFC3D[J].European Journal of Environmental and Civil Engineering,2013,17(Supp.1):282-293.
[13]MARSAL R J.Large-scale testing of rockfill materials[J].Journal of Soil Mechanics and Foundation Division,ASCE,1967,93(2):27-43.
[14]EINAV I.Breakage mechanics-Part I:Theory[J].Journal of the Mechanics and Physics of Solids,2007,55(6):1274-1297.

