改进的薄层单元在桩-土动力相互作用中的应用
苗 雨,李 威,郑俊杰,房慧明
(华中科技大学 土木工程与力学学院,湖北 武汉 430074)
1 引 言
近年来中国城市化进程逐步加快,现代建筑体量越来越大,不仅上部结构高度与体积在不断加大,其下部群桩基础的规模也越来越大。此类大体量结构物直接改变近场土特性,以往动力分析中关于刚性地基假定不再适用,而改变后的场地运动特性也将直接影响结构物振动频率、振动模态等动力特性。
在地震荷载作用过程中,由于桩身材料性能与周围土体性质相差较大,桩体与土体的变形不一致,土体在桩-土接触面上发生张开或滑移,其本构关系涉及不连续、非线性、大变形等复杂力学问题,该强非线性接触行为直接影响接触面附近土体与桩体应力状态解答,从而影响上部结构地震响应水平。同时,桩-土界面性质对桩承载与变形有着显著地影响[1-2]。因此,对于特定的桩-土-结构地震响应除了选取合适的动力本构模型外,选取能真实反应动力相互作用的桩-土接触面模型是得到正确动力响应结果的关键所在[3]。
桩-土接触面并不是在混凝土界面上的零厚度二维曲面,结构混凝土粗糙表面会对其附近土体产生一定约束作用,使该区域土体力学特性不同于其他区域土体力学特性,即真实桩-土接触面为有一定厚度且存在相关体变规律的接触带。
有限元方法为模拟该接触带提供了强大而灵活的方法。在一个有限元模型里可将上部结构、群桩基础与近场土完全耦合在一起,采用界面单元模拟桩-土接触面,无需单独对某一部分进行计算或观测。目前常用的界面接触单元有Goodman 无厚度单元[4]与Desai 薄层单元[5]。
本文在现有桩-土-结构体系地震动力相互作用研究基础上利用有限元软件ABAQUS 对桩-土-结构体系引入改进Desai 薄层接触单元进行非线性地震动力响应分析
2 改进三维Desai 薄层单元
三维Desai 薄层单元的本构关系以增量形式可表示为
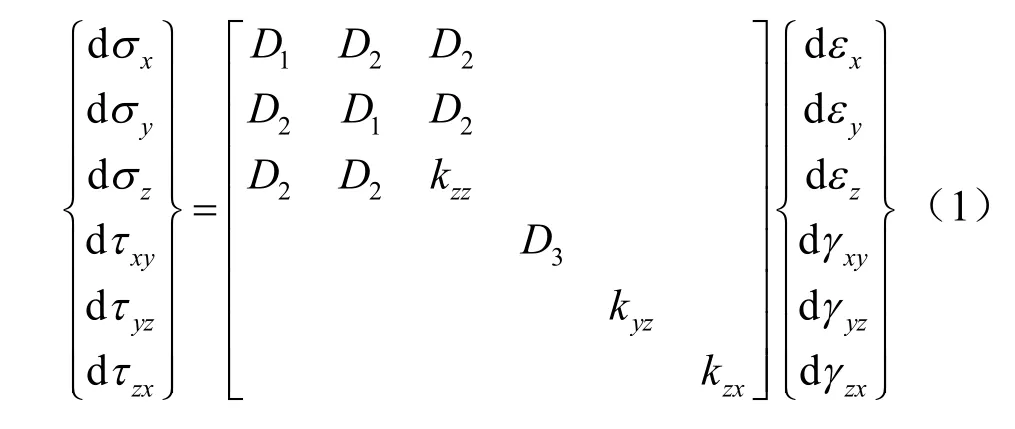
式中:z为接触面法向;D1、D2、D3、kzz、kyz、kzx均为各向异性弹性本构中弹性矩阵的弹性系数,其中
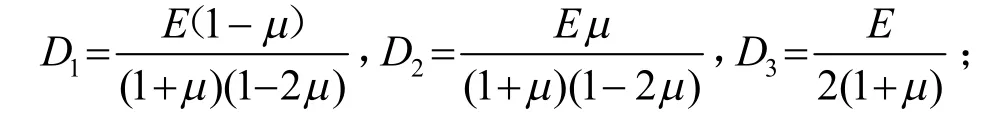
式中:E、μ 分别为弹性模量和泊松比;接触面法向刚度不宜取值过大。
Desai 认为,薄层单元法向本构与该单元相邻两侧材料性质有直接联系,因此,接触单元[Dn]可写为
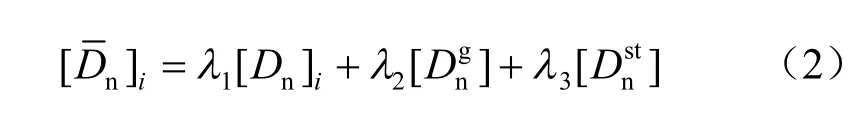
接触单元法向本构关系,借鉴Bandis[6]双曲线模型:
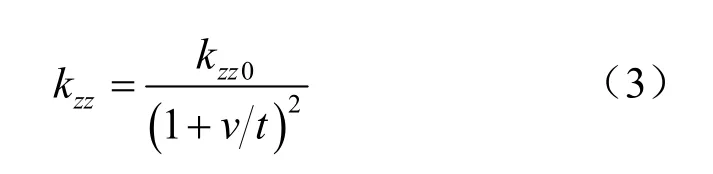
式中:kzz0为接触面初始法向刚度;可取D1;v为法向相对变形;t为接触面厚度。
接触单元两切向本构关系采用应变硬化的双曲线模型,即:
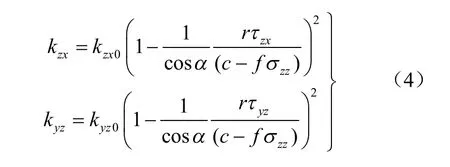
式中:kzz0和kyz0为初始切向刚度,可取D3;c为凝聚力;f为摩擦系数;α为摩擦剪切滑移角;双曲线的渐进值为(c-fσzz)/r,r为失效比。
选取的阻尼应能反映桩-土动力相互作用时桩周土非线性变化以及接触单元刚度变化[7],采用Rayleigh 阻尼,将接触单元阻尼矩阵取为
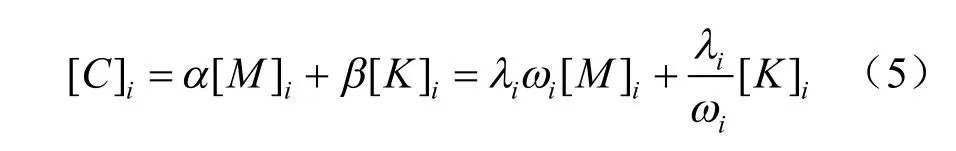
式中:λi、ωi分别为桩周土阻尼比与自振频率,在真实桩-土相互作用过程中桩周土阻尼比与土剪应变呈负相关,采用等效线性化方法处理土的阻尼比非线性问题。
Desai 薄层接触单元在桩-土接触面的行为模式以单元节点上应力-应变状态规定该单元在桩-土接触面上的4 种行为模式:黏结、滑移、张开、再闭合[8]。具体实现流程如下:
(1)在分析时程的初始状态,即薄层单元的法向应力小于抗拉强度且切向应力小于剪切强度时,接触单元与桩身处于黏结状态。
(2)当单元切向应力大于剪切强度而法向应力小于抗拉强度时,接触单元发生滑移。此时令单元切向应力等于其剪切强度,法向应力维持不变。
(3)当单元法向应力大于抗拉强度时,接触单元发生张开。而由于单元发生张开部位节点切向与法向应力将在同一个迭代步中转移至周围节点,这部分力将在下一迭代步中进行计算。发生张开的单元法向与切向刚度设置为0,直至单元节点与桩身节点距离达到一个极小值时,再恢复其法向与切向刚度,则单元又回到黏结状态。
ABAQUS 提供二次开发用户自定义单元UEL接口。用户需在该Fortran 接口下依据有限元法布置单元节点、选择位移函数、计算弹塑性矩阵、布置高斯积分点,计算出节点位移与节点力,最终需返回单元刚度矩阵与迭代残差力。
UEL 接口文件中,RHS(right-hand-side vector)表示自定义单元对整体系统方程贡献的数组。对于绝大多数非线性问题,RHS 表示在当前增量步下模型内外构型残差力大小。AMATRX 用以存放自定义单元刚度矩阵,用户计算出单元刚度矩阵后将其存放于AMATRX 中,ABAQUS 再将AMATRX 组装入总体单元刚度矩阵。AMATRX 矩阵的构造形式依赖于求解方法的选择。
本节所述改进Desai 薄层接触单元为三维八节点单元,各节点含有3 个平动自由度,与ABAQUS软件自带C3D8 实体单元自由度保持一致,可直接耦合。将本节所述改进Desai 薄层接触单元编写fortran 用户子程序UEL,并在编写 ABAQUS 主程序 inp 文件时通过“*UER ELEMET”与“*UEL PEOPERTY”命令调用。需要注意的是,由于该Desai薄层接触单元各自规定了法向与两切向本构关系,属各向异性单元,需在建模中通过“*Distribution”、“*Orientation”为改进Desai薄层接触单元指派方向。
3 三维桩-土-结构体系有限元模型参数选取
3.1 三维黏弹性动力人工边界选取
为消除地震波在人工边界上的反射,并模拟半无限地基在人工截断边界处弹性恢复能力,需对模型边界进行处理。采用由一系列并联弹簧与阻尼器组成的三维人工黏弹性边界[9],其弹簧系数与阻尼系数分别为
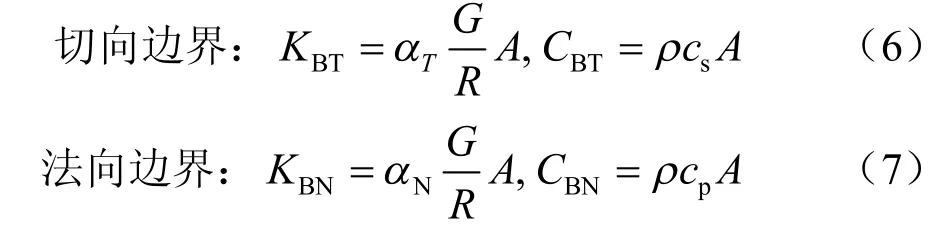
式中:KBT、KBN分别为弹簧切向与法向刚度;CBT、CBN分别为阻尼切向与法向系数;cs、cp分别为S 波、P 波波速,本算例取cs=3 500 m/s,cp=6 000 m/s;αT、αN分别为切向与法向人工边界修正参数,由于黏弹性人工边界有良好的鲁棒性,αT与αN可以在一定范围内取值,本算例αT取值范围为0.35~0.65,取αT=0.5。αN取值范围在0.8~1.2,取αN=1。R为波源至人工边界点距离,震源深度取5 000 m;G为介质剪切模量,本算例土体剪切模量取450 MPa;ρ为介质质量密度,本算例土体质量密度取2.0 g/cm3;A为边界上共用该节点单元的加权表面积。
3.2 地震动输入选取与确定
本算例所用地震波采用清华大学陆新征等[10]教授结合中国规范反应谱开发的人工地震动生成程序。该程序规定了地震动加强时间、地震动衰弱时间、地震动时长以及特征周期。中国《建筑抗震设计规范》[11]中规定湖北省武汉市抗震设防烈度为Ⅵ度,设计基本地震加速度值为0.05 g,在以时程分析进行抗震设计时对于多遇地震地震加速度时程最大值不超过0.18 m/s2。将程序设定地震动加强时间为2 s,地震动衰弱时间为10 s,特征周期取0.4 s,生成两水平向地震动,限于篇幅,只给出南北向地震波加速度时程图,如图1 所示。竖直向地震波取水平向地震波2/3。避免模型出现“偏移”现象,3条人工地震波生成后,需要对其进行基线修正。
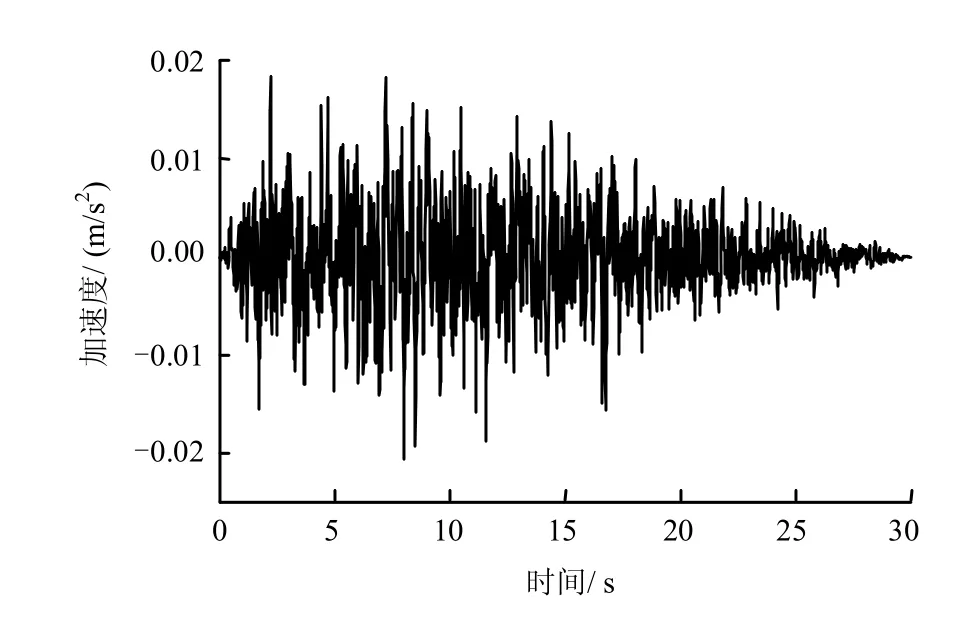
图1 南北向地震波加速度时程Fig.1 Acceleration time history of N-S earthquake wave
3.3 材料本构模型选取及相关参数确定
上部结构与桩基础混凝土采用混凝土塑性损伤模型。该模型考虑混凝土拉压性能各异,提供混凝土拉伸开裂与压缩破碎两种失效机制,可用于模拟由损伤引起的刚度退化,其屈服面由两个拉伸等效塑性应变和压缩等效塑性应变控制。混凝土塑性损伤模型基本参数见表1。

表1 混凝土塑性损伤模型基本参数Table 1 Parameters of concrete plastic damage model
土体采用等效弹性模型。等效弹性模型由一黏壶元件与一弹簧元件并联组成近似考虑土体非线性性质与滞回性质,以等效剪切模量与阻尼比将土体非线性性质等效为线性本构,以等效应变振幅描述滞回圈性质,符合中小震下砂土动力行为。参数较少,迭代计算次数较少,该模型基本参数见表2,三维等效弹性模型方程为
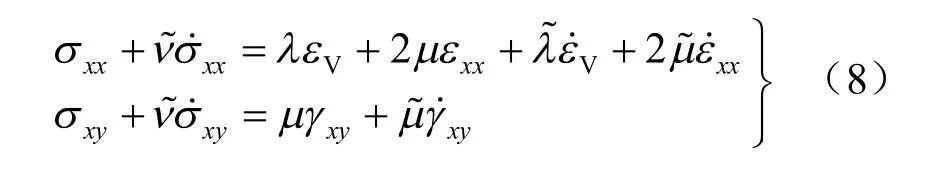

表2 等效弹性模型基本参数Table 2 Parameters of equivalent elastic model
将本节所述等效弹性模型编写fortran用户子程序UMAT,并在编写 ABAQUS 主程序inp 文件时通过“*UER MATERIAL”命令调用。
为避免三维黏弹性动力人工边界与结构物距离太近引起的边界影响与考虑地震波传输耗散阻尼因素,取模型土体尺寸大于5 倍结构物柱网距离。即水平向取50 m×50 m,竖向尺寸取30 m。结构物为8 层框架结构,柱间距为8 m,除首层外其余层高为3.3 m,首层层高为3.8 m。框架梁尺寸为300 mm×700 mm,框架柱尺寸为300 mm×300 mm,板厚取20 mm,每根柱下采用规模为2×2 的群桩基础,桩长为5 m,桩间距为0.7 m。承台尺寸为1.5 m×1.5 m×0.2 m,埋深为1 m。该模型除UEL 外所有单元采用C3D8(三维八节点)线性全积分实体单元。每个标准层划分出596 个C3D8 单元,每个桩基础划分出4 612 个C3D8 单元,土体划分出114 155 个C3D8 单元,桩周土共划分出1 560 个UEL 单元。整体模型网格图如图2 所示。

图2 整体模型有限元网格示意图Fig.2 Finite meshes of the whole model
4 算例分析
本节将讨论改进Desai 薄层接触单元对三维桩-土-结构动力相互作用(工况1)影响,并将结果与无阻尼Desai 薄层接触单元作用模型工况(工况2)、接触行为模型为硬接触与库仑摩擦工况(工况3)、接触行为模型为硬接触与无库仑摩擦工况(工况4)、非匹配网格耦合接触工况(工况5)进行比对。
图3为上部结构顶层角点位移前12 s 东西向时程曲线对比。图4为上部结构顶层角点位移前12 s南北向时程曲线对比。由图中可以看出,5 种工况下上部结构动力响应趋势与量级均相似。桩-土接触单元相比于普通接触行为模式有两点显著区别,①有接触单元工况相比于其余工况其上部结构位移峰值响应更显著;② 有接触单元工况相比于其余工况其位移时程振动分量更加丰富。这是因为无论硬接触行为法则、库仑摩擦行为法则以及非匹配网格耦合接触法则均假定两物体近似为刚体模型,三者均不考虑两物体自身本构变化对接触行为影响。因此,这些法则相比于Desai 薄层接触单元其接触约束显得更为“刚硬”。在真实的桩-土动力行为模式中,土体密度与孔隙水压力亦为随时间变化函数,而在地震时程中桩-土接触面多处随意张开、滑移、闭合也给Desai 薄层接触单元约束能力带来很大影响。
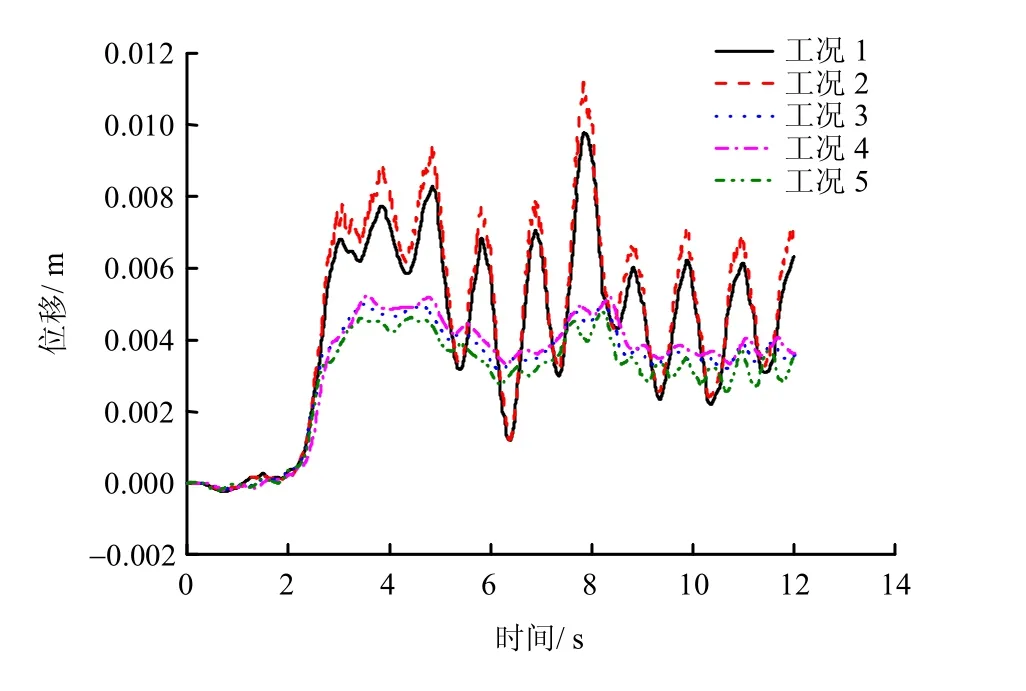
图3 上部结构顶层角点位移前12 s 南北向时程曲线对比Fig.3 Comparison of N-S displacement time history curves on the top corner point of the superstructure in the first 12 s
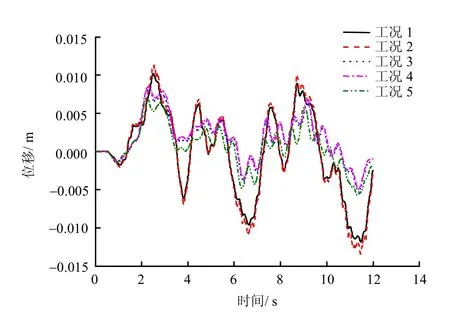
图4 上部结构顶层角点位移前12 s 东西向时程曲线对比Fig.4 Comparison of W-E displacement time history curves on the top corner point of the superstructure in the first 12 s
将5 种工况中结构物各层角柱最外侧节点东西向与南北向时程曲线提取制作成结构框架柱东西向位移包络曲线如图5 所示。由图中可看出接触单元工况相比于其余3 种工况其动力响应峰值有不同程度增大,对于接触单元工况,有阻尼峰值位移比无阻尼峰值位移在南北向与东西向均有不同程度下降。下降程度随着距离柱顶位移增大而减小。
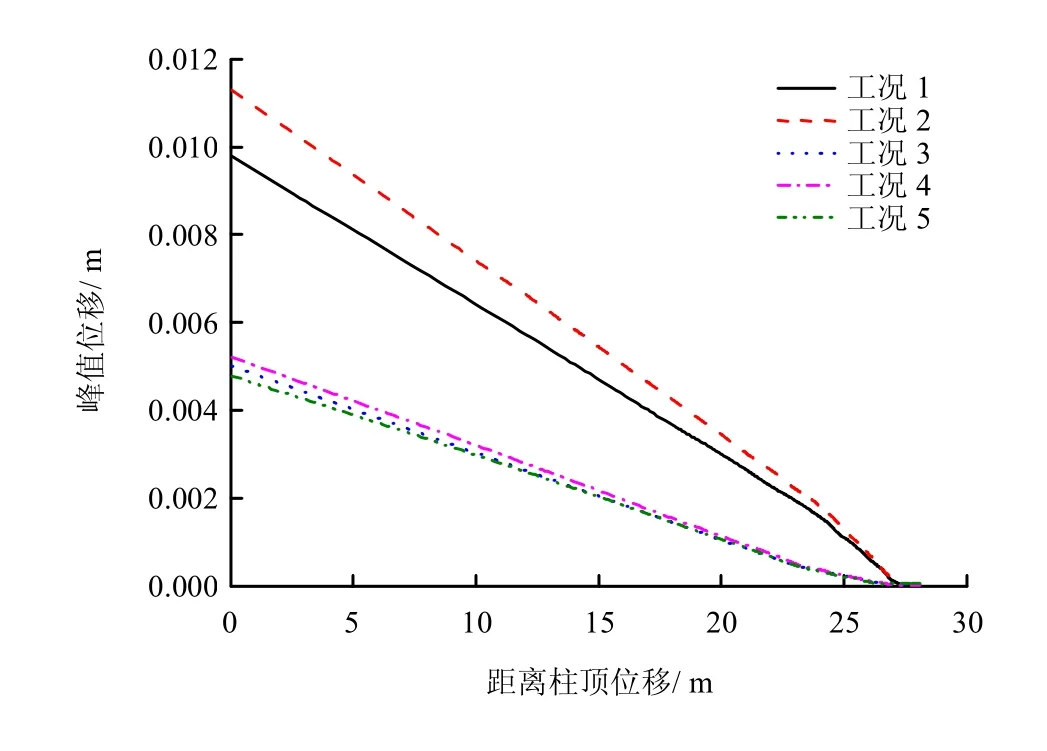
图5 框架柱东西向位移包络曲线Fig.5 Envelope curves of W-E displacement of frame column
限于篇幅,本文仅给出各层框架柱柱顶南北向弯矩包络曲线(如图6 所示)。由图中可以看出,改进Desai 单元工况各结构柱截面峰值弯矩均大于其余两种工况。最大相差约69.94%,最小相差约47.64%。此外,不同输入地震波峰值对结构物峰值剪力、峰值轴力、峰值弯矩影响详见表3。
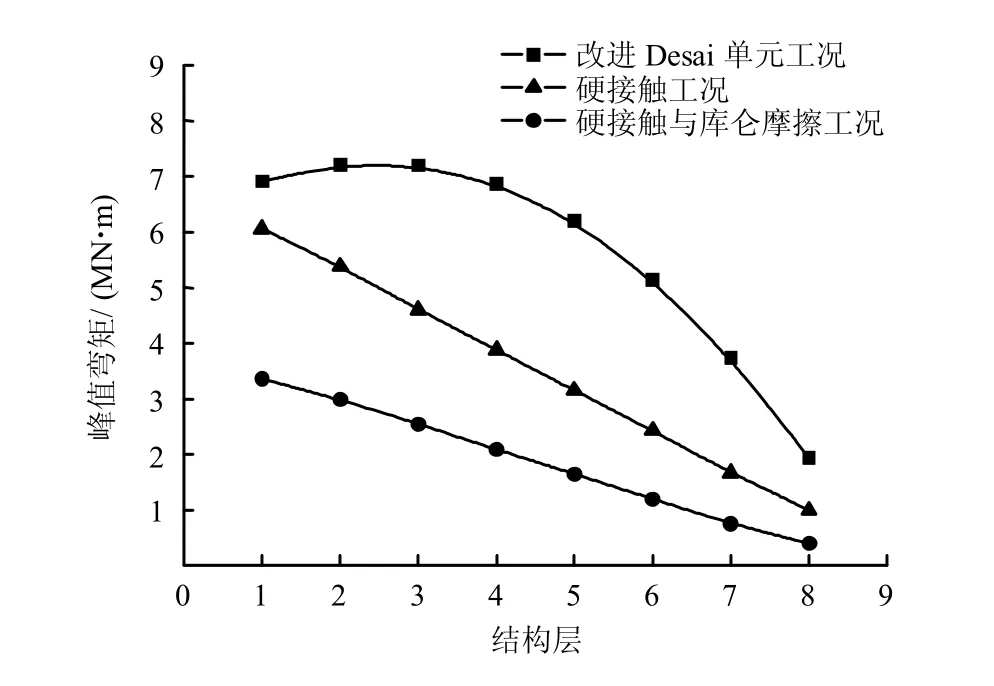
图6 各层框架柱柱顶南北向弯矩包络曲线Fig.6 Envelope curves of N-S moment on the top of each frame column
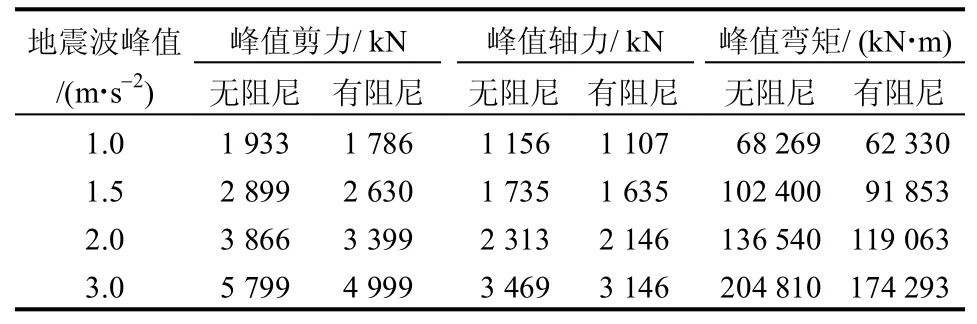
表3 不同输入地震波峰值下的结构物峰值剪力、峰值轴力、峰值弯矩Table 3 Peak values of shear force,axial force and moment of superstructure under different peak accelerations
5 结 论
(1)桩-土接触单元相比于普通接触行为模式有两点显著区别:①有接触单元工况相比于其余工况其上部结构位移峰值响应更显著;② 有接触单元工况相比于其余工况其位移时程振动分量更加丰富。
(2)相比于接触单元工况,硬接触行为法则、库仑摩擦行为法则以及非匹配网格耦合接触法低估了上部结构的动力响应峰值;对于接触单元工况,有阻尼峰值位移比无阻尼峰值位移在南北向与东西向均有不同程度下降。下降程度随着距离柱顶位移增大而减小。
(3)相对于硬接触与库仑摩擦工况、硬接触,采用改进的Desai 单元时,各结构柱截面峰值弯矩均较大。
只有对近场土动力特性与桩-土-结构动力相互作用特性有足够的认识,才能扩大其适用范围与提高计算精度。
[1]李永辉,王卫东,黄茂松,等.超长灌注桩桩-土界面剪切试验研究[J].岩土力学,2015,36(7):1981-1988.LI Yong-hui,WANG Wei-dong,HUANG Mao-song,et al.Experimental research on pile-soil interface shear behaviors of super-long bored pile[J].Rock and Soil Mechanics,2015,36(7):1981-1988.
[2]胡永强,汤连生,李兆源.静压桩桩-土界面滑动摩擦机制研究[J].岩土力学,2015,36(5):1288-1294.HU Yong-qiang,TANG Lian-sheng,LI Zhao-yuan.Mechanism of sliding friction at pile-soil interface of jacked pile[J].Rock and Soil Mechanics,2015,36(5):1288-1294.
[3]陈国兴,谢君斐,张克绪.土与结构材料界面性状的研究概况[J].世界地震工程.1994,4(1):1-9.CHEN Guo-xing,XIE Jun-fei,ZHANG Ke-xu.Review of research on the behavior of interface between soil and structural materials[J].World Earthquake Engineering,1994,4(1):1-9.
[4]GOODMAN R E,TAYLOR R L,BREKKE T L.A model for the mechanics of jointed rock[J].Journal of Soil Mechanics &Foundations Div.,1968,94(3):637-660.
[5]DESAI C S,ZAMAN M M,LIGHTNER J G,et al.Thin-layer element for interfaces and joints[J].International Journal for Numerical and Analytical Methods in Geomechanics,1984,8(1):19-43.
[6]BANDIS S C,LUMSDEN A C,BARTON N R.Fundamentals of rock joint deformation[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1983,20(6):249-268.
[7]王满生.考虑土-结构相互作用体系的参数识别和地震反应分析[D].北京:中国地震局地球物理研究所,2005.WANG Man-sheng.Identification of system parameters and analysis of seismic response considering soil-structure dynamic interaction[D].Beijing:Institute of Geophysics China Earthquake Administration,2005.
[8]金峰,邵伟,张立翔,等.模拟软弱夹层动力特性的薄层单元及其工程应用[J].工程力学,2002,19(2):36-40.JIN Feng,SHAO Wei,ZHANG Li-xiang,et al.A thin-layer element for simulation of static and dynamic characteristic of soft interaction and its application[J].Engineering Mechanics,2002,19(2):36-40.
[9]刘晶波,谷音,杜义欣.一致黏弹性人工边界及黏弹性边界单元[J].岩土工程学报,2006,28(9):1070-1075.LIU Jing-bo,GU Yin,DU Yi-xin.Consistent viscousspring artificial boundaries and viscous-spring boundary elements[J].Chinese Journal of Geotechnical Engineering,2006,28(9):1070-1075.
[10]陆新征,叶列平,缪志伟.建筑抗震弹塑性分析[M].北京:中国建筑工业出版社,2009.LU Xin-zheng,YE Lie-ping,MIAO Zhi-wei.Elastoplastic analysis of buildings against earthquake[M].Beijing:China Building Industry Press,2009
[11]住房和城乡建设部标准定额研究所.GB 50011-2010建筑抗震设计规范[S].北京:中国建筑工业出版社,2010.The Standard Quota Institute of the Ministry of Housing and Urban-Rural Development.GB 50011-2010 Code for seismic design of buildings[S].Beijing:China Building Industry Press,2010.

