主轴轴承温度场重建及其仿真研究

刘明尧，杨 顶，刘 繄

(武汉理工大学 机电工程学院，湖北 武汉 430070)



主轴轴承温度场重建及其仿真研究

刘明尧，杨 顶，刘 繄

(武汉理工大学 机电工程学院，湖北 武汉 430070)

针对主轴轴承高速运转时产生大量摩擦热，温度分布发生变化，使轴承零件产生热位移，对机床加工精度有显著影响的问题，研究了主轴轴承的温度分布规律，并对运行工况下主轴轴承的温度分布状态进行了研究，通过对主轴轴承温度场的仿真研究，实现了轴承温度场的重建。对温度测点的布置方案进行了优化，形成了轴承温度场的测量原理和方法。

主轴轴承；温度分布；温度场测量

轴承的温升和温度分布状态对轴承的性能有很大影响。主轴轴承在负荷的作用下，高速运转时会产生大量的摩擦热，导致温度分布发生变化，使轴承零件产生热位移，同时影响润滑剂的性能，对轴承的运转性能产生负面影响，影响主轴单元的加工精度。因此，主轴轴承的温度分布成为衡量机床加工精度的一个重要尺度。另外，轴承在受载情况下，承受的都是脉动循环变化的接触应力，受力不均匀引起局部温升变化，导致温度分布不均匀。文献[1]提出用热流网络方法计算轴承系统的温度分布。该方法是一种近似计算法且只适用于稳态情况。文献[2]研究了轴承结构和润滑参数对轴承温升的影响。随着计算机技术的发展，数值分析方法得到广泛应用，其中有限元法[3]、边界元法[4]、解析法[5]均可用于计算轴承的温度分布。文献[6]通过试验研究了陶瓷球轴承在数控机床高速主轴单元中的温升。OHISHI等[7]用实验方法研究了空气静压轴承主轴单元的温度分布。张伯霖等[8]对影响高速主轴单元热特性的主要因素和变化规律进行了探索。KIM等[9]分析了主轴轴承热特性对主轴单元刚度的影响，并对主轴单元的冷却及控制进行了优化设计。上述分析都没有考虑轴承在受力作用下轴承温度分布的数学描述方法，随着轴承转速的提高，轴承载荷与摩擦热的关系更加紧密，摩擦热对轴承精度的影响更加明显。笔者对运行工况下主轴轴承的温度分布状态进行了研究，对主轴轴承的温度场进行仿真研究，实现了轴承温度场的重建。对温度测点的布置方案进行了优化，形成了轴承温度场的测量原理和方法，为轴承温度场的分布式测量奠定了基础。

1 载荷作用下轴承温度分布状态分析

1.1 轴承受力分析

轴承的摩擦力矩[10]包括润滑引起的黏性摩擦力矩M0和负荷引起的摩擦力矩M1两个部分：

M=M0+M1

(1)

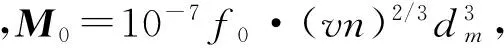
轴承摩擦力矩确定后，由于摩擦发热引起的发热量[11]按式(2)计算：

Q=1.05×10-4nM

(2)

式中：n为轴承转速；M为轴承摩擦力矩。

1.2 轴承温度场仿真分析

1.2.1 轴承有限元模型建立

以数控机床主轴常用的单列角接触球轴承7026AC为例，考虑到滚动轴承结构的复杂性，分析时对模型进行了适当简化。在忽略热辐射的条件下，轴承产生的热量在轴、轴承内圈及滚动体之间主要以热传导的方式进行传热，热量在轴承外圈与周围环境之间则以对流换热的方式散发掉。对于大型轴承，轴承内圈及滚动体相对轴而言，尺寸较小；另外，轴承的温度分布是复杂的三维问题，为了简化，假定温度分布是一维的且热传递是稳态的。因此，进行温度场分析时，在保证发热量不变的前提下，将轴承简化为圆环零件，将轴、轴承内圈及滚动体作为一个整体处理。轴承热分析的有限元模型如图1所示。

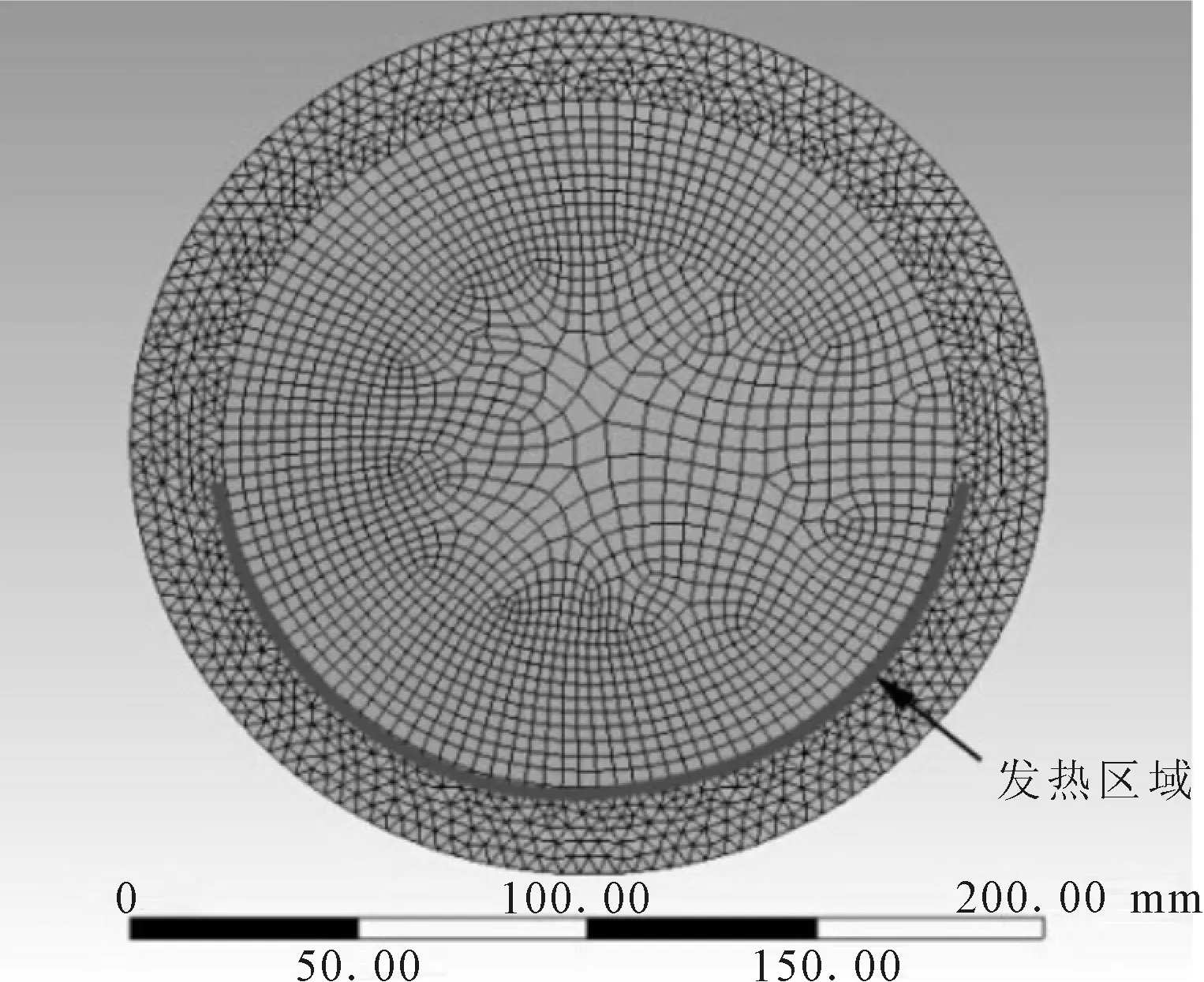
图1 轴承有限元模型

1.2.2 热边界条件的确定

轴承产生的发热量主要以热传导、热对流及热辐射3种形式传递。与轴、轴承、轴承座之间的热传导和润滑剂的强迫对流相比，热辐射的影响较小[12]，可以忽略不计，这里只考虑热传导及热对流。边界上的热传导系数已知，主轴导热系数取48W/(m·K)。与轴承相接触的流体介质的温度及换热系数已知，该边界条件为轴承与周围环境的热对流。表面换热系数按式(3)计算：

α=Nuλ/x

(3)

式中：α为表面换热系数；Nu为努塞尔数；λ为空气导热系数；x为特征长度。文献[1]指出，对于轴承与润滑剂之间的强迫对流，x取轴承的节圆直径。

由于换热系数很难由理论精确计算得到，文献[3]在实际计算换热系数时采用理论值的5～10倍。因主轴单元各部分对流条件不同，只能根据经验估计换热系数的取值范围为95～500 W/(m2·K)。根据式(3)计算并结合实验数据，最终确定换热系数为100 W/(m2·K)。轴承周围空气温度为25 ℃。材料热物性参数如表1所示[13]。

表1 材料热物性参数

1.2.3 ANSYS仿真结果

采用ANSYS软件进行仿真分析，得到如图2所示的轴承温度场分布图和如图3所示的轴承外圈温度分布曲线图。从仿真结果可以看出，在轴承最下端，受载越大的地方发热量也越大，温升也相应地增大，向两边温升逐渐减小，而轴承上半部分温度基本处于一个恒定值。

图2 轴承温度场分布图

图3 轴承外圈温度分布曲线图

2 轴承温度场重建及轴承监测点布置

轴承监测点的布置原则是在保证温度测量准确的前提下，尽可能通过较少的温度测点，即可求出轴承温度场的数学表达式，实现对轴承温度场的重建。运用Matlab曲线拟合功能对仿真数据进行拟合，得到轴承外圈温度场的数学表达式。通过比较几种常见曲线拟合方式的拟合效果，选择出最优的拟合函数。不同拟合方式所得到的拟合参数对比表如表2所示。SSE(误差平方和)和RMSE(根的均方误差)越接近于0，R2和AdjustedR2越接近于1时，拟合效果越好。

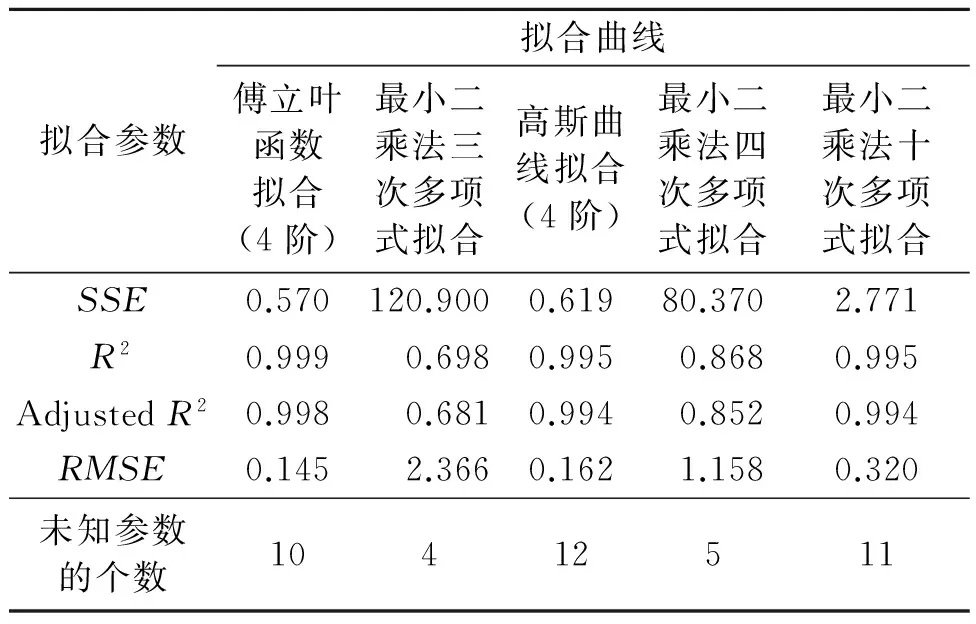
表2 拟合参数对比表

由以上不同拟合方式的拟合结果可知：傅立叶函数拟合效果最好；在最小二乘法多项式拟合方式中，虽然其表达式所含未知数少，但拟合误差过大，无法满足精度要求。

当待求解的未知参数越少时，需要布置的温度测点就越少；拟合精度越高，温度场描述越准确。根据该原则，为使拟合精度达到要求，同时使待求解的未知参数尽可能少，选择出最优的拟合函数，即傅立叶函数(4阶)逼近，其数学表达式为：

f(x)=a0+a1cos(x×w)+b1sin(x×w)+

a2cos(2x×w)+b2sin(2x×w)+

a3cos(3x×w)+b3sin(3x×w)+

a4cos(4x×w)+b4sin(4x×w)

其拟合结果如图4所示。

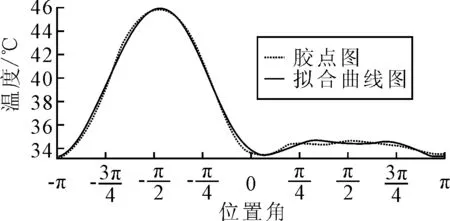
图4 拟合曲线图

求得表达式中选定参数为：a0= 37.130；a1=0.302；b1= -4.722；a2=-3.159；b2=-0.360；a3=-0.138；b3= 0.786；a4=-0.285；b4=-0.053；w=1.000。

轴承温度分布的数学表达式为：

f(x)=37.130+0.302cos(x)-4.722sin(x)-3.159cos(2x)-0.360sin(2x)-0.138cos(3x)+0.786sin(3x)-0.285cos(4x)-

0.053sin(4x);x∈[-π,π]

考虑到表达式中某些高阶项的取值范围较小，对轴承整个温度场的计算可以忽略不计。因此，轴承温度场的表达式可简化为：f(x)=A0-A1sin(x)-A2cos(2x)；x∈[-π,π]。温度场数学表达式中含有3个未知参数A0,A1,A2，因此只需要3个温度测点即可求解。在位置角ψ1,ψ2,ψ3处，布置3个光纤光栅温度传感器，测得的温度分别为T1，T2，T3。其矩阵形式为：

解得：

A0=T1+A1sinψ1+A2cos2ψ1

实验在C616普通车床上完成，时间为2014年12月18日，实验室环境温度为7 ℃。机床以750r/min的转速旋转，2h后达到热稳定状态。受条件限制，在机床空转时加载一个垂直向下、大小为3 000N的力,如图5所示。

图5 力加载装置

为了方便计算，在位置角-π，-π/2，π/2处分别安装FBG1，FBG2，FBG3共3个温度传感器。传感器安装位置如图6所示。

图6 温度传感器安装示意图

测得对应位置角的温度值分别为T1=32 ℃，T2=40 ℃，T3=33 ℃。求得A0=34.25，A1=3.50，A2=2.25。最终求得轴承温度分布数学表达式为f(x)=34.25-3.50sin(x)-2.25·cos(2x);x∈[-π,π]。

在车床的主轴轴承外圈每隔45°均匀布置8个温度测点，实测数据和计算数据对比表如表3所示。

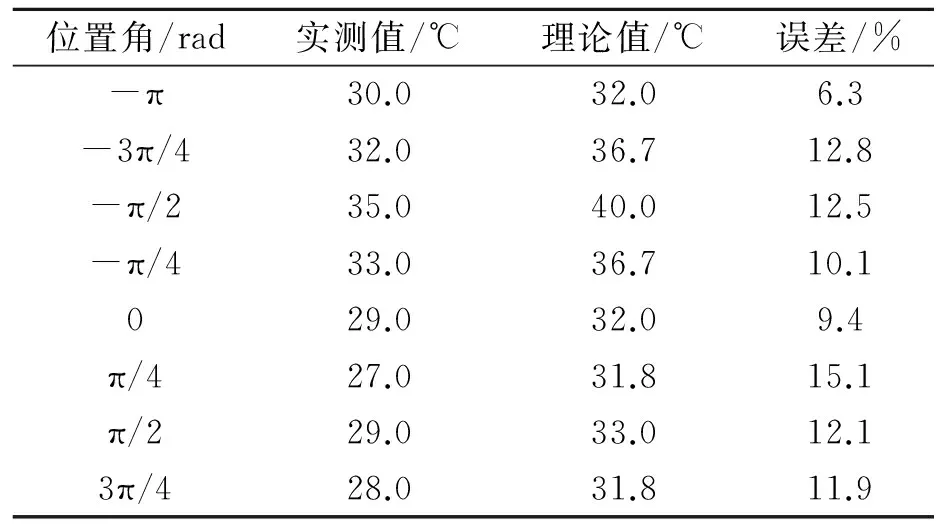
表3 实测数据与计算数据对比表

通过对比发现，最大温度差值在5 ℃内，初步分析原因，主要有以下两个方面：

(1)光纤光栅温度传感器未经封装，灵敏度及测量的精确性受到限制，给测量的准确性造成一定的影响；

(2)温度传感器安装在轴承座上，与外部环境接触，极大地受到外部环境热对流的影响，导致测量的温度较理论计算值低。

3 结论

(1)利用有限元法建模，对主轴轴承进行仿真分析，得到轴承在运行工况下的温度分布状态，为轴承温度场的分布式测量提供了理论基础。

(2)通过较少的温度测点即可求得轴承的整个温度场分布，得到轴承温度场的数学描述方法，优化了温度测点的布置。

[1] HARRIS T A, KOTZALAS N M. Rolling bearing analysis[M]. Boca Raton:Taylor & Francis,2007:31-37.

[2] 蒋兴奇,马家驹.高速角接触球轴承速度性能试验研究[J].中国机械工程,2002(12):15-20.

[3] 杨咸启.轴承系统温度场分析[J].轴承,1997(3):14-18.

[4] 杨咸启.用边界元法分析滚动轴承热传导[J].轴承,1990(4):2-4.

[5] 吉田孝文.机床主轴用高速滚动轴承的温度解析方法[J].国外机床轴承,1999(21):30-40.

[6] 孙红.陶瓷球轴承在高速主轴单元中的应用研究[J].制造技术与机床,2001(11):14-18.

[7] OHISHI S, MATSUZAKI Y. Experimental investigation of air spindle unit thermal characteristics[J]. Precision Engineering,2002(1):49-57.

[8] 张伯霖,夏红梅,黄晓明.高速电主轴设计制造中若干问题的探讨[J].制造技术与机床,2001(7):24-29.

[9] KIM S M, LEE S K. Prediction of therm-elastic behavior in a spindle bearing system considering bearing surroundings [J].International Journal of Machine Tools & Manufacture, 2001(7):14-25.

[10] 邓四二,贾群义.滚动轴承设计原理[M].北京:中国标准出版社,2008:97-145.

[11] 刘泽九,贺士荃,刘晖.滚动轴承应用[M].北京:机械工业出版社,2007:25-38.

[12] 刘耀中.高碳铬轴承钢滚动轴承零件热处理技术发展与展望[J].金属热处理,2014(1):25-29.

[13] 秦大同,谢里阳.机械设计手册[M].北京:化学工业出版社,2013:145-168.

LIU Mingyao:Prof.; School of Mechanical and Electronic Engineering, WUT, Wuhan 430070, China.

[编辑：王志全]

Reconstruction of Temperature Field for Bearing of Machine Tool Spindle

LIUMingyao,YANGDing,LIUYi

Bearing is an important part of mechanical equipment. In the spindle system, great frictional heat generates during the high-speed operation. Thermal displacement of the bearing parts is caused by the change of temperature distribution, and has a significant impact on the machining accuracy. Temperature distribution of spindle bearings was researched. And the temperature distribution of spindle bearings in operating conditions was studied. The reconstruction of bearing temperature field was achieved by the simulation study of spindle bearing temperature field. And layout scheme of temperature measuring points was optimized.

spindle bearings; temperature distribution; measurement of temperature field

2015-03-22.

刘明尧(1963-)，男，湖北仙桃人，武汉理工大学机电工程学院教授.

湖北省重点科研基金资助项目(2013CFA047).

2095-3852(2015)05-0533-04

A

TH39

10.3963/j.issn.2095-3852.2015.05.002