基于遗传算法的计算机网络可靠度优化分析

查道贵，许彩芳

宿州职业技术学院计算机信息系，安徽宿州，234101



基于遗传算法的计算机网络可靠度优化分析

查道贵，许彩芳

宿州职业技术学院计算机信息系，安徽宿州，234101

利用遗传算法建模，分析排队通信数据模型并计算容量分配和路由选择时间；采用遗传算法和遍历配法竞争选择，确定适应值函数与范围，得到相关的收敛的探索方式。利用遗传运算对计算机网络进行优化并调整数据传输，判断信道连通性。仿真结果表明：遗传算法具有搜索高效、求解便捷和算法结构简便等优势，对全局进行计算时，能够得到最优近似值。

计算机网络；遗传算法；可靠度；优化

所谓计算机网络可靠性是指在操作方式、负载条件、维修方式、湿度、温度和辐射等规定条件下，一个季度或者1 000小时等规定时间内，计算机网络满足通信要求与保持连通的能力。计算机网络可靠性的测试通常包括网络生存性、连通性，在多种模式中网络元件有效性和抗破坏性等方面内容[1]。

国外对计算机网络可靠性的研究最早源自电信网络交换的研究，并将网络的连通性作为计算机网络可靠性的测度。国内对计算机网络可靠性的研究最早由著名科学家钱学森提出，但主要应用于军工领域，1956年张公绪提出通信网络割集的概念和算法。之后，更多国内外科研人员、专家学者开始研究这个课题，出现了许多新的算法，如不交和算法、因子分解算法、完全状态枚举算法、容斥原理算法等。

1 计算机网络可靠度

计算机网络可靠度与计算机网络的可靠性不同，它是指在操作方式、负载条件、维修方式、湿度、温度和辐射等规定条件下与一个季度、1 000小时等规定时间内，计算机网络对规定功能予以完成的概率。

如何提高和优化计算机网络的可靠度，是计算机网络使用与研究关注的重要问题。本研究根据顺序服务措施和原则利用遗传算法建立数学模型，忽略延时并简化计算机网络中通信NP难题(非图灵机上的多项式时间算法问题)与存储节点信息，得到收敛的相近的最佳结果。

2 问题描摹

2.1 问题假设

(1)假设在网络中的传输节点间只有一条直线传输链路，却存在有多条信息传输信道，由此方便通过建立数学模型来对网络传输的信息进行描述；(2)假定各传输信道的稳定性良好，且各节点能有效进行数据信息的传输；(3)网络中的信道介质长度与网络可靠度存在间接数据交换关系；(4)在设备出现故障时，与数据传输信道无关，即通信信道与网络有故障与工作两种状态[2]。

2.2 建立数学模型

计算机网络信道链路中的成本矩阵可用方程式表示：

(1)

其中，Cij表示结点j,i表示间链路介质成本,C0表示信道介质成本矩阵。

用数学计算公式表示网络信道链路介质见方程式(2)和(3)：

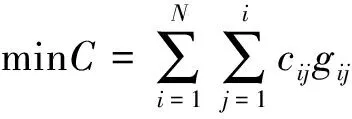
Diαij(i,j=1,…,N)

(2)

(3)

以上两个公式中，N表示计算机网络传递结点数，C表示通信信道中信息的成本，Diαij表示结点j和i间链路介质数，β、α表示结点可靠度在计算机网络中的约束常数。如果gij=1，那么节点j和i间存在直线链路；如果gij=0，那么以上两节点不存在直接链路。

依照以上计算方法，计算链路介质的方程式为：

(4)

其中，rji表示网络结点间链路可靠度(1≤i≤m，1≤j≤n)，R0表示网络可靠度矩阵[3]。

如果计算机网络状态为可用，则处于网络状态的计算机结点皆相互连通，各可用状态的结点能组成一棵生成树，网络互联正常并能确保正常工作。在正常运行的互联网过程中，在L′⊆L成立的状态下，互联网线路能够正常传输信息。在这种情况下，互联网中所有结点均为正常工作状态，其可靠度表示为：

(5)

其中，ni表示网络第i结点，P(ni)表示网络链路中介质可靠度，N表示网络结点数。

在方程式(4)中，如果计算机网络为正常工作状态，那么互联网中数据传输最大化为R,而且C≤C0,此时网络为正常工作状态，用方程式表示为：

(6)

其中，li表示网络中第i条线路介质，Ω表示正常工作状态下计算机网络的所有集合[4]。

3 基于遗传算法的计算机网络可靠度优化

3.1 通信过程优化的数学建模

在信道中，为优化数据传递，简化计算机网络中通信NP难题与存储节点信息，根据顺序服务措施及原则，应用遗传算法建立数学模型。计算分析数据排队模型，为方便描述节点信息传输与信道链路信息处理的延时忽略，用方程式(7)表示容量分配与路由选择的时间计算：

(7)

其中，K表示可选容量类型数，λm表示互联网节点m报文送达率，fk表示信息流量，D表示企业信息传递延时，Vk表示信息流量的更改。

然而，方程式(7)中，其约束条件还有以下几点，需要优化多信道传输可靠度：

运用方程式(7)可获得一个非线性方程，该方程含有分配容量与选择路由，属于有约束条件且优化后的数学建模模型，可见，采用遗传算法能够解决该问题。

3.2 求解过程

遗传算法是一种随机搜索算法，它是通过遗传机理和生物自然选择理念而得出的并以交换个体信息与群体搜索的方式，搜索出互联网中最优点且可确保算法设计最优化。具体过程如下：

Begin：i←0初始化，p(i)计算，p(i)若条件不满足，则需要终止条件→begin→p(i)重组，获得c(i)→计算c(i)→从c(i)与p(i)中对p(i+1)进行选择→i←i+1→end

3.3 优化设计

依照遗传算法优化计算机网络可靠性，可以满足优化互联网的需求，且能够达到较好效率。该方法可以明显改善互联网数据传输效率，在具体设计中，首先将遗传算法控制参数与相关数据输入，确定初始群体适应值函数与范围，利用遍历匹配法来竞争选择，再实施杂交处理且必须满足与全局相近的有收敛条件的最优解[5]。

3.3.1 基因表达

从根本上说，基因表达是对互联网传输予以确定的主要优势，本研究通过二进制一维编码，对计算机互联网N个结点互联网基因予以确定，具体设计见表1。

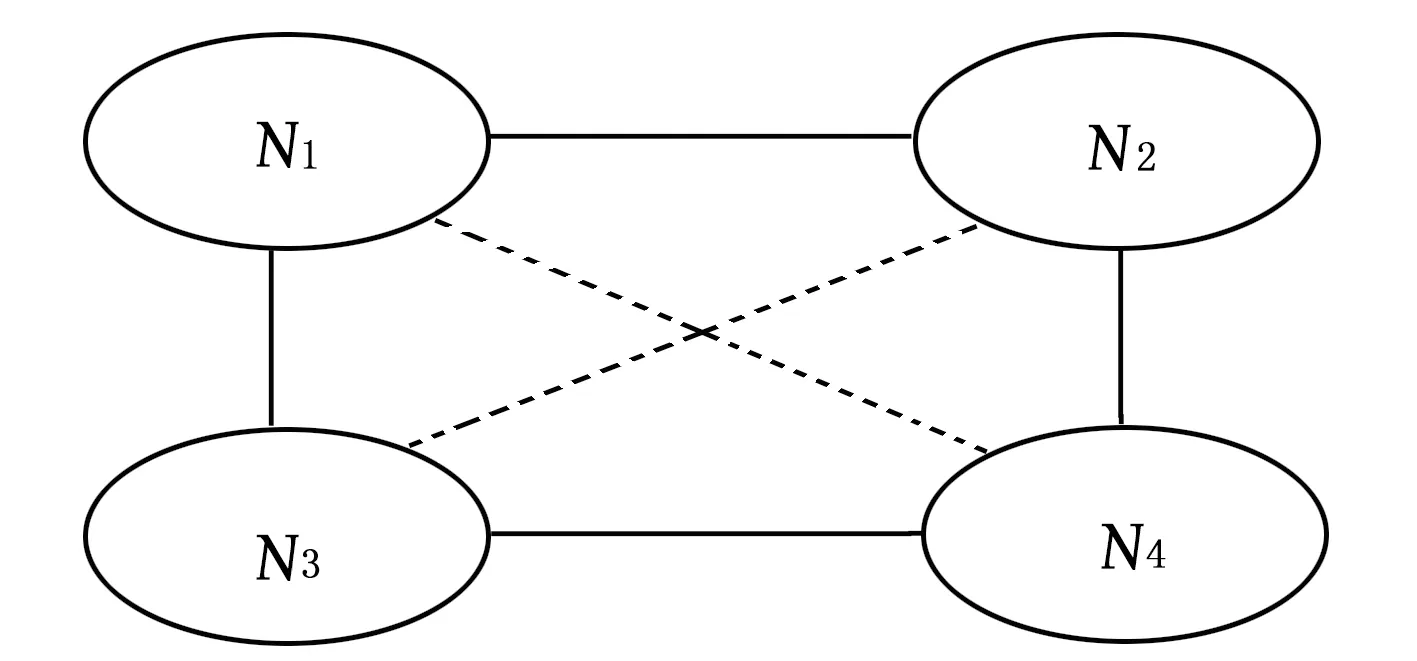
图1 基因结点网络图

表1 计算机互联网基因结点

假定互联网信道传输中有4个结点(n1,n2,n3,n4)，则将这4个互联网基因结点会转化为一个基因，见表2，从而形成一个网络结构图，见图1。

表2 4个节点的互联网基因结点

3.3.2 选择适值函数

算法确定的基础是适值函数。适值函数对遗传算法中发生的数据欺骗可以有效预防，以降序的方式对数据个体在初始种群中的成本值进行排列，设定最小排序成本个体编码值为1，设定最大排序成本编码值为POP-size,那么其适值函数用方程(x-1)/(POP-size-1)=f(x)表示。在该公式中，POP-size表示种群规模，x表示网络成本中数据个体的排序位置，且其约束条件是POP-size≥x≥1。

3.3.3 网络优化中的遗传运算

遗传运算在对计算机网络优化中主要分为变异与交叉两种形式。

(1)交叉。([1,N])是实现数据交叉的范围,采用随机交叉法确定基因交叉位置且实现数据交换，能确保计算机网络数据互连互通性，但有时一些临界数据并不说明网络数据连通，会发生网络错误，因此应对算法进行调整。

(2)变异。首先明确变异的基因范围和具体变异数目，再依照所选基因片段取代原先基因。具体操作包括以下几步：

①如果数据变异基因是x，那么x=[x1，x2，…，xk];

②依照数据变异基因数目，对整数进行随机选取，k∈[1,n],u∈[1,n];

④若不能实现步骤③，可以转至步骤②[6]。

3.3.4 进化运算

运用转轮选择运算并依照适值函数运算法提出相关假设条件，选择时，任意基因选择概率均与其适值呈正比，适值是fk的基因。适值fk和选择概率Pk及与种群编码排序范围的关系用方程式表示为：

3.3.5 算法优化调整

依照算法优化结果，调整相应数据传输，分析算法中所有基因表达式，以此判断信道是否连通[7]。

①若gij=1,那么执行原交叉，实施基因数据变异，最终完成数据操作；

②若gij=0，依照遗传算法计算与分析要求，使gij=1；

③若gij=1，实施数据交换，使gij=0;

④若无法实现步骤③,那么需要判断与测试网络信道的连通性。

4 仿真举例

依照以上遗传算法计算，并根据假设，构建计算机网络通信系统，运用遗传算法进行仿真实验。如果计算机网络系统结点有6个，以实验的方式优化计算机网络可信度，多次计算实验结果。在计算机网络可靠度优化实验中应用遗传算法，使网络稳定性与可靠性得到有效提升，所得结果见如下矩阵：

运用可靠度矩阵R0对所测可靠度数据进行计算[8]，计算得出的结果见如下矩阵 ：

依照上文的假设可得出：计算机网络结点N为6，优化互联网通信信道可靠度约束常数：β=2，α=2。计算互联网通信信道时，如果遗传操作代数是100次，对其进行仿真计算求解，能够将互联网信道链路总成本计算出来，最终计算得出其值为46，可以确保网络信道可靠度max为0.885，互联网系统信息传输具有较为可靠的安全性与完整性。这充分表明，在网络信道可靠度的优化中，利用遗传算法可以满足互联网信息传输需求。

5 结 语

与其他算法相比较，遗传算法有以下特点：

(1)遗传算法可以提升信息传输速度。通过仿真实验与实际计算分析，遗传算法具有较为简单的结构，在互联网信息传输中比较适用。尤其本身具有搜索高效、操作简单以及适用性强等特点，可以确保互联网传输效率的有效提升。与传统互联网传输计算方法相比，遗传算法的优势较为明显，运用该算法，互联网计算时间得到有效缩短，进一步提高了信息计算速度且优化了计算效果；能明显改善互联网传输方式，有效地提高互联网操作性能。

(2)遗传算法具有较强的计算信息传输的适用性。遗传算法大大降低了互联网成本，在原有基础上，不断提升网络可信度，对互联网性能进行不断优化，而且还能兼顾矩阵可靠度优化问题、链路介质成本问题和数学模型求解等相关问题。

[1]江逸楠，李瑞莹，黄宁，等．网络可靠性评估方法综述[J]．计算机科学，2012，39(5)：9-18

[2]吴俊，段东立，赵娟，等．网络系统可靠性研究现状与展望[J]．复杂系统与复杂性科学，2011，8(2)：77-86

[3]刘东，丁照宇．基于改进遗传算法的可靠性网络优化设计[J]．计算机技术与发展，2007(1)：63-68

[4]武小悦，张维明，沙基昌．具有节点失效的网络可靠度的信息交互算法[J]．国防科技大学学报，1999(2)：111-114

[5]金庆风，刘胜利．基于可靠性理论的计算机通信网络分析及多目标优化[J]．微型电脑应用，2009(1)：19-73

[6]孙力娟，王汝传．量子计算与遗传算法的融合及其在计算机通信网优化中的应用[J]．电子与信息学报，2007(4)：920-923

[7]刘雅琴，迟洪钦．最优合并构成的有序遗传算法[J]．上海师范大学学报:自然科学版，2001(4)：89-92

[8]肖宇峰，张华．基于二元决策图的节点不可靠网络可靠度计算[J]．计算机工程，2015，41(1)：87-91

(责任编辑：汪材印)

2015-08-21

安徽省教育厅自然科学研究项目“皖北旱地小麦秸秆腐化剂选择及直接还田配套技术的研究”(KJ2014A254)。

查道贵(1975-)，安徽安庆人，硕士，讲师，主要研究方向：计算机应用。

TP393.02

：A

：1673-2006(2015)12-0093-04

10.3969/j.issn.1673-2006.2015.12.025