基于灰色最小二乘支持向量机的大坝变形预测
任 超 梁月吉 庞光锋 蓝 岚
1 桂林理工大学测绘地理信息学院,桂林市建干路12号,541004 2 广西空间信息与测绘重点实验室,桂林市建干路12号,541004
大坝在施工或运行过程中会由于各种原因发生不同程度的形变,及时掌握大坝变形的演变规律并作出准确预报,对大坝安全具有重大意义。大坝变形与水压、温度、时效因素之间具有复杂密切的关系,而这些因素往往具有较强的随机性和难以解析的非线性,导致大坝变形较为复杂,难以直接建立较为准确的变形量与影响因素之间的非线性关系模型。针对这一问题,国内外学者已研究出多种模型,如时间序列模型、回归分析模型、灰色模型、神经网络和支持向量机等[1]。但每一种模型都存在自身的局限性,难以全面考虑负荷的变化趋势和影响因素,直接通过建立单一模型进行变形预测不易得到令人满意的结果。灰色模型提供了在贫信息情况下解决系统问题的新途径,通过自身“累加生成”的特点,能够将复杂的原始数据化为较符合客观规律的时间序列数据,但不足之处是仅适合解决呈指数增长趋势的实际问题。而实际的大坝变形规律往往与指数规律差别较大,不利于灰色模型的建立和预测,且模型参数的求解也存在一定的理论缺陷[2]。支持向量机(support vector machine,SVM)是Cortes等[3]提出的一种机器学习算法,能较好地解决小样本、非线性和高维模式识别等实际问题,已在变形预测中得到广泛应用。Suykens等[4]在Vapnik 统计学习理论的基础上提出最小二乘支持向量机(least square support vector machines,LS-SVM),将SVM 的二次规划问题转换为求解线性方程组的问题,降低了计算的复杂性,提高了求解速度。
基于上述研究,本文提出基于灰色最小二乘支持向量机的大坝变形预测新算法,通过利用灰色预测方法中的“累加生成”原理对原始序列进行预处理,以削弱序列中随机扰动因素的影响,得到规律性较强的新序列,进而建立LS-SVM 预测模型。同时,考虑到LS-SVM 的参数优化问题,采用网格搜索法[5](grid search)进行寻优,该方法用于小样本数据预测时比遗传算法、混沌优化算法较有优势。通过两个算例,并与灰色GM(1,1)和单一最小二乘支持向量机对比分析,验证该算法的可行性和有效性。
1 灰色最小二乘支持向量机预测模型
1.1 灰色最小二乘支持向量机原理
设大坝原始位移时间序列为:

式中,n为大坝位移的监测期数。首先对原始位移序列进行一次累加:
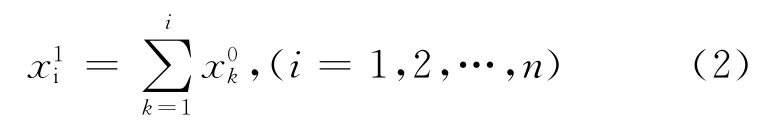
得到规律性更强的新序列:
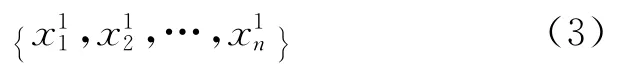
然后,以新序列的前m期为训练集,后(n-m)期为测试集,利用拟合能力更好的LS-SVM 建立预测模型。设样本训练集为{(xi,yi)|i=1,2,…,m},其中,xi∈Rn为输入向量,yi∈R为输出向量,用非线性映射φ(·)将样本输入从原空间映射到高维特征空间,构造出LS-SVM 的回归函数为[4,6]:
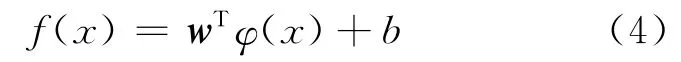
式中,φ(x)为满足Mercer条件的核函数,w为超平面的权值向量,b为偏置项。
在LS-SVM 估计中,回归问题可以等价为最小化下面泛函:
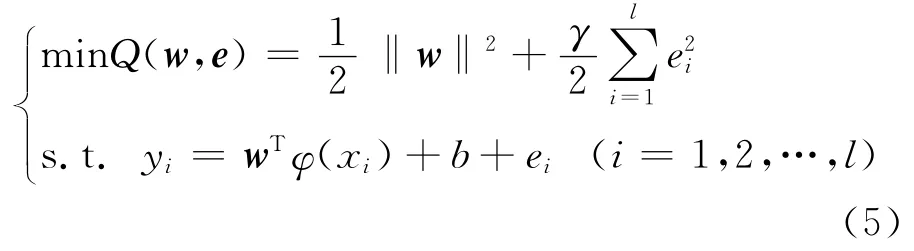
式中,γ为正则化参数,ei为误差项。构造式(5)的Lagrange函数为:
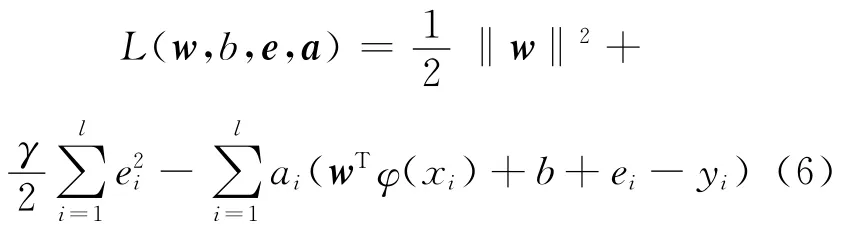
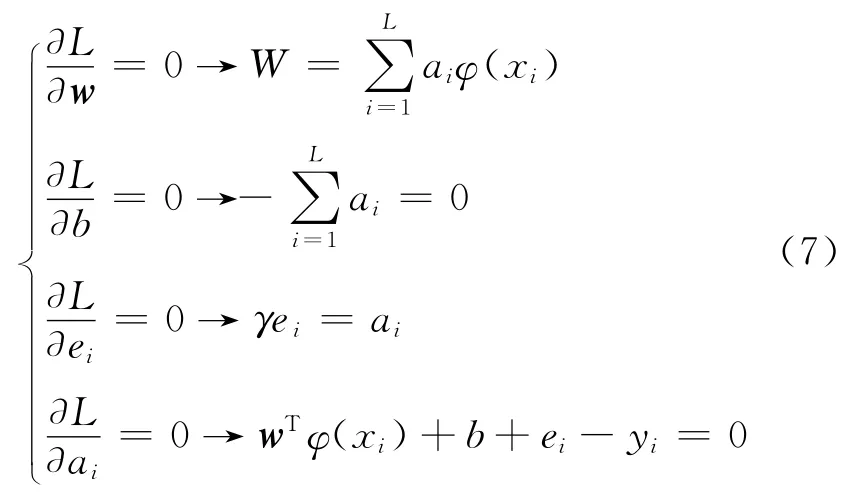
式(7)消去w和ei得到线性方程组:
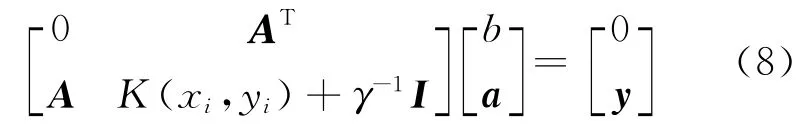
由于B=K(xi,yi)+γ-1I为对称的正定矩阵,利用最小二乘运算求解式(8)可得:
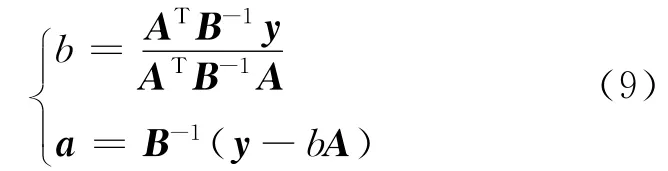
求解式(6)得到LS-SVM 的估计函数为:
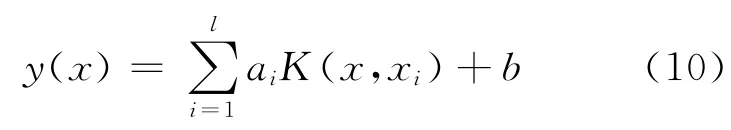
最后,计算累加序列的预测值ym+j,j=1,2,…,n-m,并对其进行累减还原,得到原始序列的预测模型:
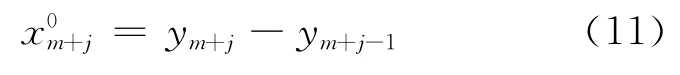
1.2 LS-SVM 参数的优化
最小二乘支持向量机的性能很大程度上取决于核函数K(x,y)、核参数σ和正则化参数γ的最优选择。目前,核函数主要有3 类:多项式核函数、径向基核函数和线性核函数,其中径向基核函数能较好地反映模型的复杂程度,预测效果比较好。因此,选定其为LS-SVM 的核函数。考虑到参数选取问题,采用网格搜索法进行参数优选。其基本原理是将σ和γ在一定的范围划分网格并遍历网格内所有点进行取值,对取定的σ和γ采用交叉验证方法[7]获取训练均方误差作为网格点计算的目标函数,最终取训练集验证均方误差最低的那组σ和γ作为最佳参数。该方法寻优过程中各组参数相互解耦,较好地避免了由于参数多或参数之间可能出现耦合而引起的多解性问题,便于并行计算,且运行效率较高。具体步骤如下[5]:
1)设定参数σ和γ的选择范围和参数步长。本文寻优过程分为粗选和精选两步,设定σ的寻优区间为[0 ,1010],γ的寻优区间为[0 ,1010];粗选格点数为1010×1010,步长为1;精选格点数为1010×1010,步长为0.1。
2)由于寻优过程是一个遍历过程,因此,参数初始值的选取对结果没有影响。此搜索过程选取的初始值为σ=0,γ=1,选择第一个交叉验证网点位置,通过交叉验证方法获取训练均方误差(MES)作为网格点计算的目标函数,并计算所有的网格点。
3)选取均方误差最低的一组(σ,γ)为最优参数。若选取的参数达不到精度要求,则以选择的参数为中心网格点,在较小的范围内构建新的二维网格平面重新计算目标函数,再次选取均方误差最低的参数。如果满足精度要求,则停止,否则继续重复以上步骤,最终获取精确的参数σ和γ作为最优值。
2 模型预测流程
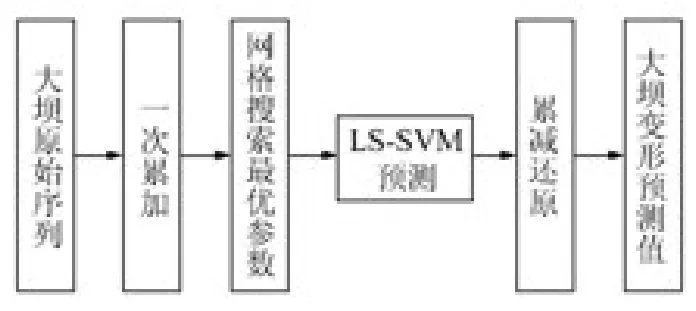
图1 模型预测流程图Fig.1 Flow chart of model prediction
3 算例分析
3.1 算例一
以文献[7]中某大坝径向变形监测数据进行实验。该大坝共布设C06和C11两个监测基准点,在大坝中部及其两侧分别布设3 个监测变形点OP03、OP04与OP05。各监测点的切向与径向定义为切向(t)和径向(r)坐标系。为充分反映大坝变形特征,本文采用位于拱坝圆弧顶部监测点OP03径向的变化数据(2001-12-31~2002-01-20),径向正轴方向指向雅砻江上游方向,如图2所示。
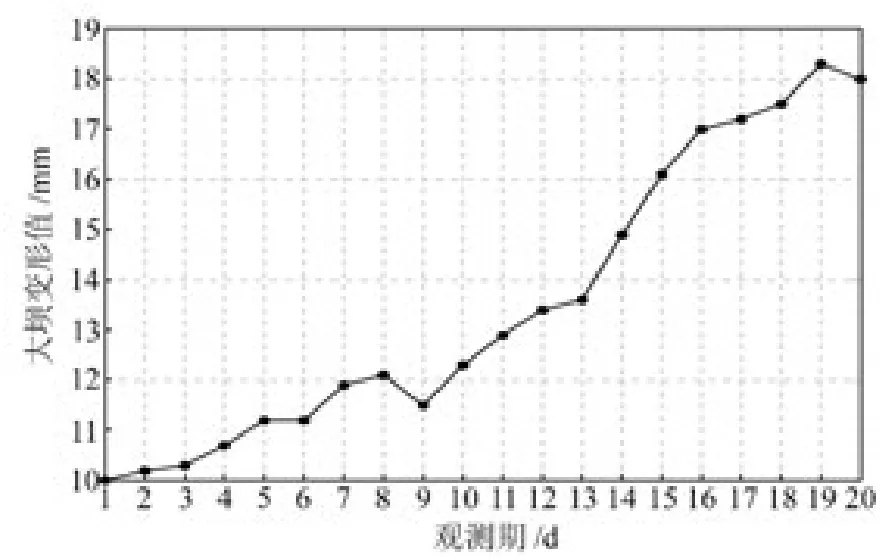
图2 大坝变形径向位移序列Fig.2 Deformation of the dam radial displacement sequence
由图2可看出,该大坝位移序列总体呈增长趋势,只有第6期、第9期和第20期有所下降,波动性较弱,大坝最大变形值为18 mm,最小为10 mm,差值为8 mm。采用灰色预测方法中的“累加生成”原理对序列进行一次累加得到如图3所示的结果。由图3可见,经一次累加生成的新序列曲线较为光滑,变化规律更为明显,有利于模型的建立和分析。
为验证本文提出的基于灰色最小二乘支持向量机在大坝变形预测中的可行性,建立3种方案进行算例分析比较:方案1——灰色GM(1,1);方案2——单一LS-SVM 预测模型;方案3——灰色最小二乘支持向量机预测模型。各方案采用前12期监测数据进行建模训练,后8期作为测试样本。经网格搜索法得到,方案2 的最优参数σ为45.265,γ为425 316.516;方案3的最优核参数为10 648.167,正则化参数为6 540 666.247。3种方案的预测结果见表1。
由表1可知,方案1预测不稳定,预测值和实际值偏差比较大,最大残差达到-1.85mm。方案2和方案3优于方案1,而方案3的预测结果最好,残差最小值为0.02mm,最大值仅为0.39mm。
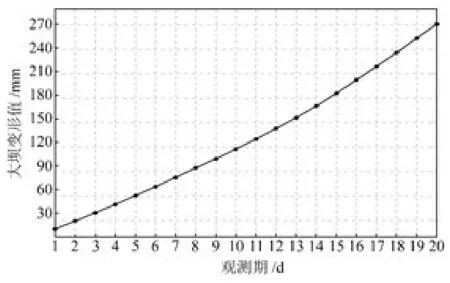
图3 一次叠加结果Fig.3 The results of a superposition
3.2 算例二
以文献[8]中某大坝水平位移变形监测数据为例(2003-01-06~2003-01-26)。该大坝共布设7个水平位移监测点,由于各点变化规律大致相同,本文仅选择D4点进行分析,如图4所示。
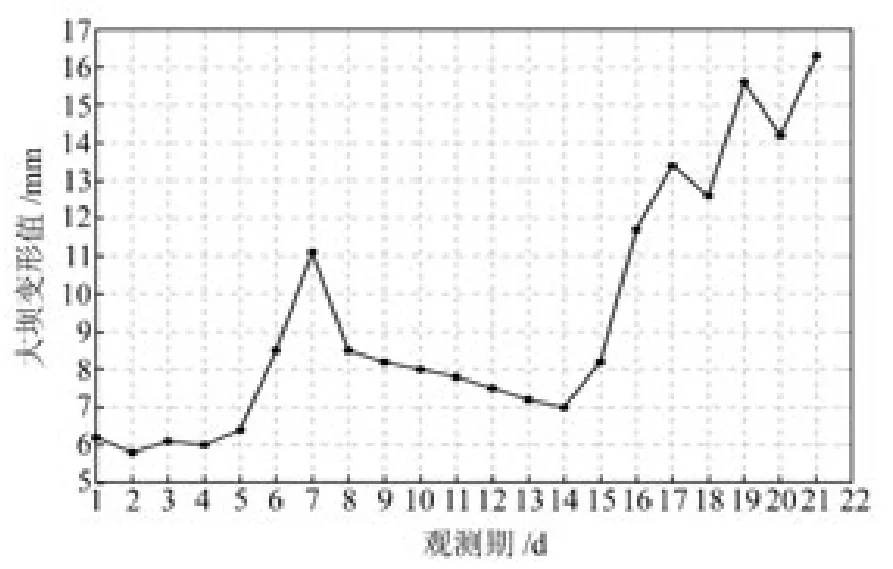
图4 大坝变形水平位移序列Fig.4 Deformation of the dam horizontal displacement sequence
从图4可看出,该大坝水平位移序列的第1~5期和第8~14 期变化都比较平缓,而第6、7期和第15~21期波动大。显然,如果用传统的预测模型,难以真实反映大坝变形的规律。对大坝原始位移序列进行一次累加得到如图5所示的结果。由图5可知,对于波动性较强、不稳定的大坝位移序列,经一次累加后变得较为光滑,有效减弱了原始序列的随机性,使离乱的原始数据中蕴涵的规律能够充分显露出来,突出了大坝变形规律。
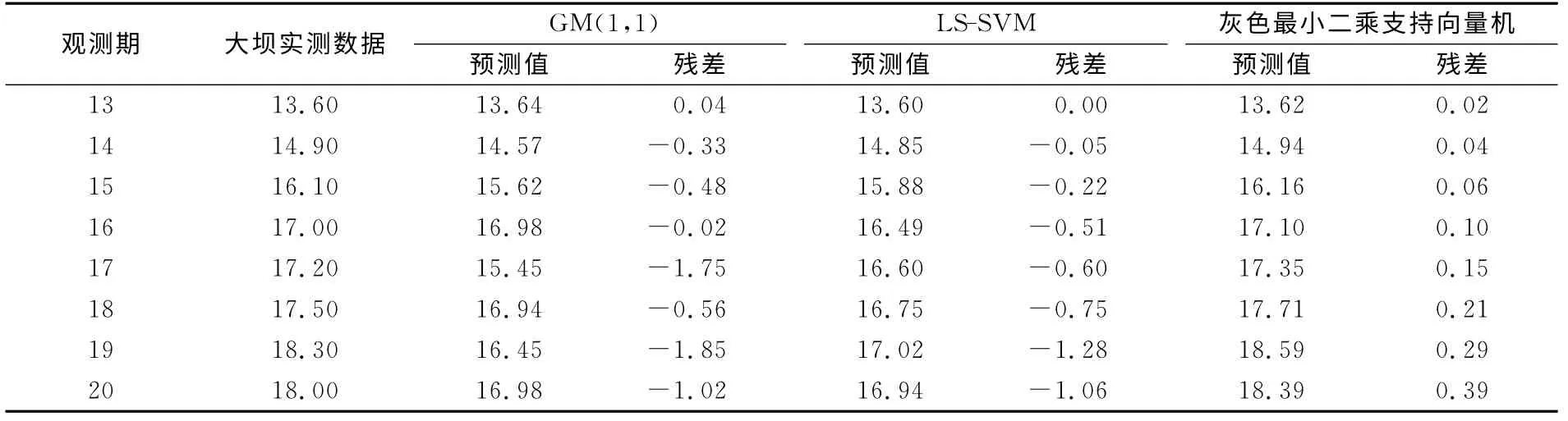
表1 各模型计算结果对比/mmTab.1 The contrast of each model calculation results/mm
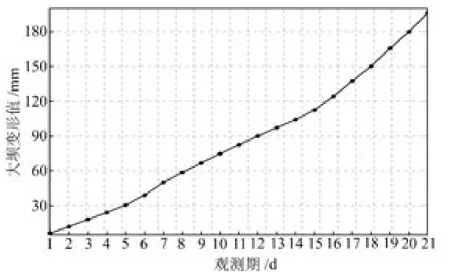
图5 一次叠加结果Fig.5 The results of a superposition
同算例一,建立3种方案进行比较。采用前12期监测数据进行建模训练,后9期作为测试样本。3种方案的预测结果见表2。同理得到,方案2的最优参数σ为108.526,γ为25 412.613;方案3的最优核参数为7 256.758,正则化参数为5 625 282.435。预测结果见表2。
从表2可看出,方案1和方案2预测不稳定,部分预测值和实际值偏差比较大,方案1最大残差达到-2.11 mm,方案2 残差最大为-1.43 mm。方案3残差最小值为0.01 mm,最大值仅为0.53mm。可见,对于波动较大和不稳定的大坝变形序列,灰色GM(1,1)的预测结果已远远偏离监测值,单一最小二乘支持向量机的部分预测结果也不够稳定,而灰色最小二乘支持向量机模型的预测效果较好,能够保证较优的局部预测值。
为进一步综合评定本文算法的性能,采用均方根误差和平均绝对误差两项指标进行评定(表3)。
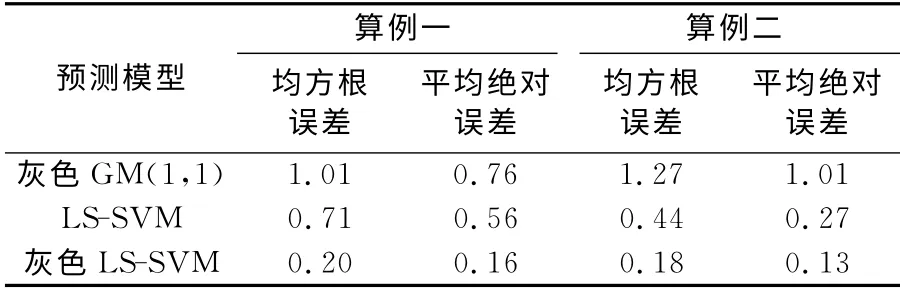
表3 各模型精度对比/mmTab.3 The contrast of each model precision/mm
由表3 可知,灰色GM(1,1)的预测精度较低,两个算例的均方根误差分别为1.01 mm 和1.27mm,单一最小二乘支持向量机表现出较好的预测精度,优于灰色GM(1,1)。而本文算法的预测精度明显较高,均方根误差分别为0.20mm和0.18mm,平均绝对误差分别仅为0.16mm 和0.13mm。可见,灰色最小二乘支持向量机预测模型在一定程度上保证了较好的全局预测精度。综上,新算法通过采用灰色原理对原始序列进行预处理,能有效削弱原始序列的随机性并增加规律性,利用最小二乘支持向量机优良的学习性能,能紧跟数据的变化规律。同时,对于不同尺度变化的大坝变形预测,效果都比较好。新算法无论是预测结果还是预测精度,都优于灰色GM(1,1)和单一最小二乘支持向量机,能在一定程度上有效解决复杂的大坝变形问题,当直接建立LSSVM 预测模型无法满足精度要求时,可以采用此算法。
4 结 语
针对大坝变形具有随机性和非线性等特点,本文将灰色理论和最小二乘支持向量机相结合引入到大坝变形短期预测。经理论和算例分析,并与灰色GM(1,1)和单一最小二乘支持向量机对比表明,传统的灰色GM(1,1)预测模型由于自身存在的理论缺陷,预测效果和实际偏差较大,难以解决复杂的变形问题;单一最小二乘支持向量机的预测效果和实际值较为接近,体现出LS-SVM在解决小样本、贫信息和多维数的复杂非线性问题中的优势;而本文新算法不仅引入灰色预测方法独特的数据生成方式,增加原始数据的规律性,减少数据的随机性,且充分发挥了LS-SVM 强大的非线性映射能力,预测精度优于灰色GM(1,1)和单一最小二乘支持向量机。同时,采用网格搜索方法可快速地选取LS-SVM 的最佳参数。
[1]马文涛.基于小波变换和GALSSVM 的边坡位移预测[J].岩土力学,2009,30(2):394-398(Ma Wentao.The Slope Displacement Prediction Based on Wavelet Transform and GALSSVM[J].Rock and Soil Mechanics,2009,30(2):394-398)
[2]张大海,江世芳,史开泉.灰色预测公式的理论缺陷及改进[J].系统工程理论与实践,2002,22(8):1-3(Zhang Dahai,Jiang Shifang,Shi Kaiquan.Theoretical Defect of Grey Prediction Formula and Its Improvement[J].System Engineering Theory and Pratice,2002,22(8):1-3)
[3]Cortes C,Vapnik V.Support Vector Networks[J].Machine Learning,1995,20(3):273-297
[4]Suykens J A K,Vandewalle J.Least Squaresupport Vector Machine Classifiers[J].Neural Processing Letters,1999,9(3):293-300
[5]Liu X L,Jia D X,Li H.Research on Kernel Parameter Optimization of Support Vector Machine in Speaker Recognition[J].Science Technology and Engineering,2010,10(7):1 669-1 673
[6]Brabanter K,Brabanter J,Suykens J A K,et al.Approximate Confidence and Prediction Intervals for Least Squares Support Vector Regression[J].IEEE Transactions on Neural Networks,2010,22(1):110-120
[7]Ito K,Nakamo R.Optimiznig Support Vector Regression Hyperparameters Based on Crossvalidation[C].International Jonit Conference on Neural Networks,2003
[8]蒋廷臣,张勤,周立,等.基于小波方法的非线性回归模型研究[J].测绘学报,2006,35(4):337-341(Jiang Tingchen,Zhang Qin,Zhou Li,et al.The Nonlinear Regression Model Based on Wavelet Method Research[J].Acta Geodactica et Cartographica Sinica,2006,35(4):337-341)
[9]焦明连,蒋廷臣.基于小波分析的灰色预测模型在大坝安全监测中的应用[J].大地测量与地球动力学,2009,29(2):115-117(Jiao Minglian,Jiang Tingchen.The Grey Prediction Model Based on Wavelet Analysis in the Application of Dam Safety Monitoring[J].Journal of Geodesy and Geodynamics,2009,29(2):115-117)

