基于MATLAB的自动机后坐到位缓冲动力学仿真

山西中北大学机电工程学院 齐清 姚养无

引言

随着步枪的不断发展，它的性能在不断提高。现在好多国家致力于小口径步枪研究，虽然现在步枪后坐力已经很大程度上减小，但是对于一些普通人来说还是较大，甚至一些妇女害怕去射击。

当步枪在发射弹丸时，武器系统要承受发射的后坐力。武器的威力越大，后坐力也就越大，武器系统振动就越大，也就越难操控，这将在很大程度上影响武器的射击精度，降低武器系统的作战效能。因此，大幅度减小武器发射时的后坐力成为武器发射技术研究的一项长期任务。目前常用的减小自动武器后坐力的技术主要有：前冲击发技术、浮动自动机技术、膛口制退技术、液压缓冲技术等。但利用自动机后坐到位缓冲来实现减小后坐力还较少见到。

自动机后坐到位仍具有一定的速度，此时就会和枪身发生撞击，这个撞击力最终会传到射手身上，对射手产生一个冲击力，同时这个撞击力会使枪身发生抖动，从而影响连续射击的精度。本文通过在MATLAB里建立后坐动力学模型对弹簧液压缓冲器和弹簧缓冲器进行动力学计算，在10mm行程里将自动机速度从4m/s降为2m/s，考察两种缓冲器的缓冲效果（本文仍然采用后坐到位时产生撞击来保证自动机可靠性的理念）。

1 弹簧液压缓冲器结构原理

弹簧在后座部分储存复进能量，而液体在后坐和复进过程中吸收机械能能量并转化为热能，复进时提供阻力以降低缓冲器复进到位的速度，从而减小复进到位的撞击力。由于液压阻力的自适应性，在后坐过程中可以适应不同环境下后坐速度的差。

图1 弹簧液压缓冲器结构原理图

弹簧液压缓冲器结构如图1所示，Ⅰ腔和Ⅱ腔充满液压油，当自动机要后坐到位时撞击活塞向左运动，此时工作腔Ⅰ内的液体被挤压形成液体压力，并通过变深度沟槽和固定流液孔流入Ⅱ，液体压力作用在活塞上形成后坐时的液压阻力。液压阻力、缓冲簧力和自动机复进簧共同组成自动机的后坐阻力。当后坐到位时，缓冲簧被压缩储存缓冲器复位的能量，此时腔Ⅰ的液体全部被挤入腔Ⅱ。缓冲器复位时，在缓冲簧力的作用下，活塞向右运动，腔Ⅱ内的液体被挤压，压力上升，形成复进时的液压阻力，使得复进速度平缓，此时腔Ⅱ的液体流回腔Ⅰ。

2 弹簧缓冲器结构原理

弹簧缓冲器在后坐时弹簧被压缩吸收并储存后坐能量，形成后坐阻力，复进时弹簧舒张将吸收的能量释放，为缓冲器复位提供作用力，其缺点是弹簧力过大，使复进的速度过大，从而使缓冲器复位时的撞击力很大。弹簧缓冲器结构如图2所示。

图2 弹簧缓冲器结构原理图

3 弹簧液压缓冲器动力学模型

3.1 液压阻力

弹簧液压缓冲器动力学分析的核心部分就是液压阻力的求解，液压阻力可以由液压阻力公式求得。其中K为修正系数，一般取1.2~1.6，这里取1.4，ρ 为液体密度，取1170kg/m3，A0为活塞工作面积，ax为流液孔面积，v为活塞运动速度。

3.2 缓冲簧力

经过多次MATLAB仿真，刚度K取5000N/m，初力F0取50N获得的效果较佳。

3.3 复进簧力

根据某枪的复进簧参数选取刚度Kf为267N/m，初力Ff为61.5N。

3.4 摩擦阻力

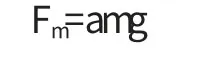
其中a取0.56，后坐时阻力方程为：

缓冲器复位时的阻力方程为：

建立动力学微分方程组：

其中v为后坐速度，x为后坐位移。

4 弹簧缓冲器动力学模型

缓冲簧力Fk=Kx+F0

其中刚度K取35000N/m，初力F0取50N。

复进簧力、摩擦力同上述弹簧液压缓冲器一样， 最后的后坐阻力为：Fr=Fk+Ff+Fm。

缓冲器复位时的阻力方程为：Fr=-Fk-Ff+Fm。

建立动力学微分方程组：

其中v为后坐速度，x为后坐位移。

5 运用MATLAB进行仿真

用MATLAB编写程序，应用四阶龙格库塔对上述动力学微分方程进行求解，设定初始位移和速度分别为0和4m/s。后坐部分（自动机和缓冲器活塞杆）质量为0.5kg。在缓冲行程为10mm的情况下，通过曲线拟合一条流液孔面积变化曲线，使得缓冲后的速度降到2m/s的同时后坐阻力较为平稳。拟合的流液孔面积变化曲线如图3所示，得到弹簧液压缓冲器后坐及复位的速度—时间曲线（图4），位移—时间曲线（图5），后坐阻力—时间曲线（图6）。结果如下。

图3 流液孔面积变化规律

图4 弹簧液压缓冲器速度—时间曲线

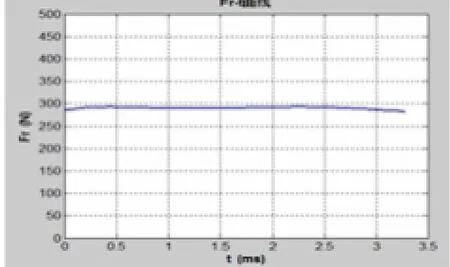
图6 弹簧液压缓冲器后坐力—时间曲线

图5 弹簧液压缓冲器位移—时间 线

弹簧缓冲器的仿真结果如下：

图7 弹簧缓冲器速度—时间曲线

图8 弹簧缓冲器位移—时间曲线

图9 弹簧缓冲器后坐力—时间曲线

6 结果分析

由图4和图7可以看出两种缓冲器均使得自动机速度从4m/s降到2m/s。

由图6与图9的最大后坐力比较不难发现，弹簧液压缓冲的最大后坐力为292.5N，而弹簧缓冲器的最大后坐力为460N，弹簧液压缓冲器较单纯的弹簧缓冲器后坐力降低36.4%。从图中不难发现弹簧液压缓冲的的后坐力较为平稳，而弹簧缓冲器的后坐力一开始比较小，随后上升比较快。由此可见弹簧液压缓冲器性能优于弹簧缓冲器，而且通过调节不同位置流液孔的大小，可以灵活地调节后坐阻力的变化。

上述通过对弹簧液压缓冲器和弹簧缓冲器在自动机后坐时的缓冲效果研究，为缓冲器的选择提供了一些依据。

[1]高跃飞.火炮后坐装置设计[M].北京：国防工业出版社,2010.

[2]王亚平,徐诚,王永娟,姚养无.火炮与自动武器动力学[M].北京理工大学出版社,2014.

[3]陈泽,占海明.详解MATLAB 在科学计算中的应用[M].北京：电子工业出版社,2011.

[4]步兵自动武器及弹药设计手册[K].国防工业出版社,1977.

[5]王刚,姚养无,张伟.反器材步枪应用弹簧液压缓冲器理论分析[J].华北工学院学报,2003：24（3）227-229.