基于互信息的PCA方法及其在过程监测中的应用

童楚东，史旭华

（宁波大学信息科学与工程学院，浙江 宁波 315211）

基于互信息的PCA方法及其在过程监测中的应用

童楚东，史旭华

（宁波大学信息科学与工程学院，浙江 宁波 315211）

主元分析（PCA）是一种经典的特征提取方法，已被广泛用于多变量统计过程监测，其算法的本质在于提取过程数据各变量之间的相关性。然而，传统PCA算法中定义的相关性矩阵局限于计算变量间的线性关系，无法衡量两个变量间相互依赖的强弱程度。为此，提出一种新的基于互信息的PCA方法（MIPCA）并将之应用于过程监测。与传统PCA所不同的是，MIPCA通过计算两两变量间的互信息来定义相关性，将原始相关性矩阵取而代之为互信息矩阵，并利用该互信息矩阵的特征向量实现对过程数据的特征提取。在此基础上，可以建立相应的统计监测模型。最后，通过实例验证MIPCA用于过程监测的可行性和有效性。

主元分析；数值分析；过程系统；互信息；故障检测；统计过程监测

引 言

近年来，针对以主元分析（PCA）为代表的多变量统计过程监测方法的研究已经受到了工业界和学术界的广泛关注，其基本思想都是从工业过程采集的数据中挖掘出能反映过程运行状况的潜在信息[1-2]。这类方法通常是在分析高维过程数据特征后，按照一定的方式将其投影降维至低维子空间，并将获得的信息以统计量的形式提供给操作人员。它不需要过程的机理模型，因而很适合于监测现代大型复杂化工业过程[2-4]。

通常来讲，PCA这种经典的特征提取方法是通过计算过程数据集的协方差矩阵或相关矩阵，再利用矩阵的特征向量确定降维投影的方向。它所提取的潜隐变量（或称主元）能体现原始数据空间的相关性特征。虽然，PCA方法用于分析过程数据时意义明确，易于实施，但是，计算变量间的协方差或相关系数只能反映变量之间的线性关系，无法衡量变量间的非线性关系[5]。因此，传统的PCA方法用于提取数据特征时具有很大的局限性。以核PCA（kernel PCA, KPCA）方法[6]为基础的非线性过程监测方法虽然能有效应对非线性过程数据，但是针对映射后的高维空间数据变量间的相关性，KPCA方法依旧计算的是相关系数，仍未涉及变量之间的非线性相关性。值得注意的是，KPCA在建立模型时，需要人为地设定核函数及其参数，不同的参数设置会直接影响到KPCA方法的故障检测效果[7]。此外，其他借鉴和学习技巧的非线性过程监测算法，如Kernel Dissimilarity[8]、核独立元分析[4]等已被相继提出并用于解决非线性过程监测问题。

在信息论领域里，互信息是一种很有用的信息度量，它可以用来解释一个随机变量中包含的另一个随机变量的信息量[9]。互信息这种度量相关性的方式在于衡量两个变量间的共同拥有的信息，不局限于单纯的线性关系，对变量之间的非线性关系也能进行评估。互信息是一种无参数、非线性的测度指标，目前，它已经在数据分析与建模领域引起了较多的关注[10-11]。此外，多变量统计过程监测领域也有一些借鉴互信息分析处理过程数据的研究成果[12-13]。

本文针对传统PCA算法定义相关性矩阵只考虑变量间线性关系的不足，提出一种基于互信息的PCA算法（MIPCA）用于统计过程建模。具体来讲，该算法首先计算过程数据集两两测量变量间的互信息，并组建相应的互信息矩阵。然后，对该互信息矩阵进行特征值分解，并选取少数几个占主导地位的特征向量作为降维投影方向。最后，对所提取的成分信息和模型残差信息分别构造统计量作为过程监测指标。值得注意的是，用于监测模型残差变化的传统指标，即平方预测误差（SPE或Q），已不适合监测MIPCA模型的残差。因为，传统Q统计量假设模型残差各向同性且方差最小[14]。为此，本文在MIPCA模型的基础上，进一步地对模型残差进行奇异值分解，然后对非零奇异值对应的成分建立T2统计量进行监测。最后，利用Tennessee Eastmann（TE）[15]仿真实验平台对比分析MIPCA与其他方法（PCA和KPCA）的监测效果，验证该方法的有效性。

1 基本方法

1.1 主元分析（PCA）

PCA是一种经典的数据降维方法，其提取的主元可以摒除原始数据空间的冗余信息而保留大量的方差信息，并且各主元变量相互正交[16]。假设X∈Rn×m（n为样本数，m为变量数）是一个经过标准化处理后的数据矩阵，通过对X进行奇异值分解，可建立PCA统计模型，即[1]

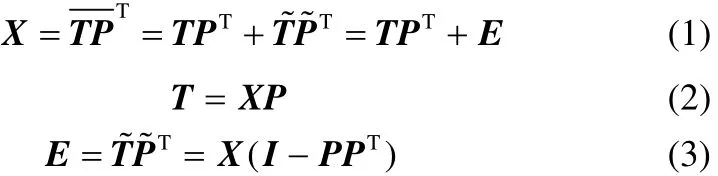
式中，T∈Rn×d和P∈Rm×d分别是主元得分矩阵和载荷矩阵，分别是残差得分矩阵和载荷矩阵，E∈Rn×m为残差矩阵，d＜m为选取的主元个数。式（1）说明X在载荷矩阵各向量方向上的投影即是得分矩阵。在求解PCA模型的过程中，主元载荷向量实际上是X的协方差矩阵C

前d个最大特征值Λ=diag{λ1,λ2,…,λd}所对应的特征向量。因此，所投影得到的主元能体现X中各变量间的相关性。

当PCA统计模型应用于故障检测时，需要对主元和残差信息分别构建T2统计量和Q统计量，即

从上两式中可以发现，2T和Q指标分别定义了平方马氏距离和平方欧式距离。对应控制限的确定方法可参考文献[1]。

1.2 互信息（MI）

互信息（MI）是信息论里一种有用的信息度量，它可以看成是一个随机变量中包含的关于另一个随机变量的信息量，或者说是一个随机变量由于已知另一个随机变量而减少的不肯定性。设两个随机变量x和y的联合分布为p(x,y)，边缘概率分别为p(x)和p(y)，互信息I(x,y)则定义成

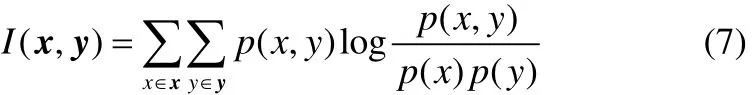
若x和y之间不存在重叠的信息，即相互独立时，互信息值等于0。反之，若两者间的相关性越高，互信息值越大。由式（7）可知，求解(,)Ix y需要已知变量x和y的分布密度概率，这在实际中通常是很难满足的，常用的解决方法是使用核密度估计方法来确定对应的概率值。

2 基于MIPCA的过程监测方法

2.1 MIPCA算法

互信息可以用来衡量变量间共有的信息量，它所定义的相关性不局限于线性关系。因此，利用互信息定义相关性矩阵具有比较大的优势，这也就是本文所提出的MIPCA算法的基本出发点。将式（4）中协方差矩阵各元素替换为互信息，即

其中，Ci,j为相关性矩阵C中的第(i,j)个元素，I(xi,xj)为测量变量xi和xj的互信息值。在本文中，互信息的计算直接采用MATLAB工具箱MIToolbox[17]。

与PCA算法类似，MIPCA求解投影向量的问题可以转化为如下特征值问题，即

式（9）中前k个最大的特征值γ1≥γ2≥…≥γk所对应的特征向量A=[α1,α2,…,αk]即是MIPCA算法的投影向量。基于此，即可建立如下MIPCA模型

其中，Y=XA为MIPCA算法的潜隐变量所组成的矩阵，F∈Rn×m是模型残差矩阵。Y和F分别定义了MIPCA模型的特征子空间（feature subspace，FS）和残差空间（residual subspace，RS）。

2.2 基于MIPCA模型的过程监测方法

当MIPCA用于在线监测新采集的样本数据x∈Rm×1时，需首先将其投影至特征子空间中，

new并建立如下监测统计量

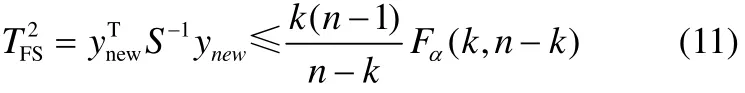
其中，ynew=ATxnew，S为式（10）中Y的协方差矩阵，Fα(k,n−k)表示自由度为k和n−k的F分布在置信限α下的取值。

通常情况下，式（6）中定义的Q统计量可用来监测MIPCA模型残差空间的变化情况，但是F中有不可忽略的方差信息。因而，需要对残差作进一步的处理。利用奇异值分解可以将F表示成如下形式

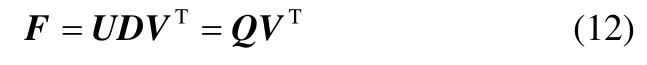
其中，Q=UD=FV=X(I−AAT)V，对角矩阵D∈R(m−k)×(m−k)对角线上的元素为m−k个非零奇异值，V∈Rm×(m−k)则由这m−k个非零奇异值所对应的向量组成，且相互正交。那么新样本xnew所对应的残差信息就被进一步的表示成

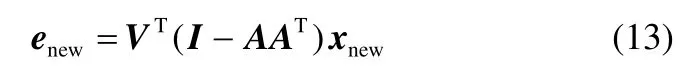
由于残差量各方向上的方差大小不一，可对式（13）构造如下平方马氏距离统计量

相比之下，传统的Q统计量采用的是平方欧式距离，要求残差信息的方差各向同性且大小可忽略，没有充分考虑残差量中方差大小不同所带来的影响。另外，统计量的控制限确定方式与式（11）类似。

3 仿真实验研究

为了测试各种不同监测方法的有效性和优越性，一个合适的测试平台必不可少。在目前发表的众多论文中，TE仿真过程是一个被学者们广泛采纳的测试平台，这主要是因为它的反应过程和生产结构都是非常复杂的，已经成为测试不同控制方法和过程监测策略的标准实验平台[18-20]。TE过程的流程示意图如图1所示，主要由连续搅拌反应器、产品冷凝器、气液分离塔、汽提塔和离心式压缩机等5个生产单元组成。TE过程可连续测量22个过程变量和12个操作变量，还可以仿真模拟21种不同的故障类型，详细资料可参见文献[18]。在本文的研究中，选取过程可连续测量的33个变量作为监测变量，详情可参考文献[7]。过程的测试数据集可从网站http://web. mit.edu/braatzgroup/links.html上下载。

离线建模阶段，利用正常工况下的960个样本建立PCA、KPCA和MIPCA的过程监测模型以作对比分析用。其中，PCA和MIPCA模型选取的潜隐变量个数都取为9，KPCA模型的高斯核函数参数c与潜隐变量个数d设定值参考文献[21,22]，考虑两组不同的参数设定值，置信限α统一取值99%。

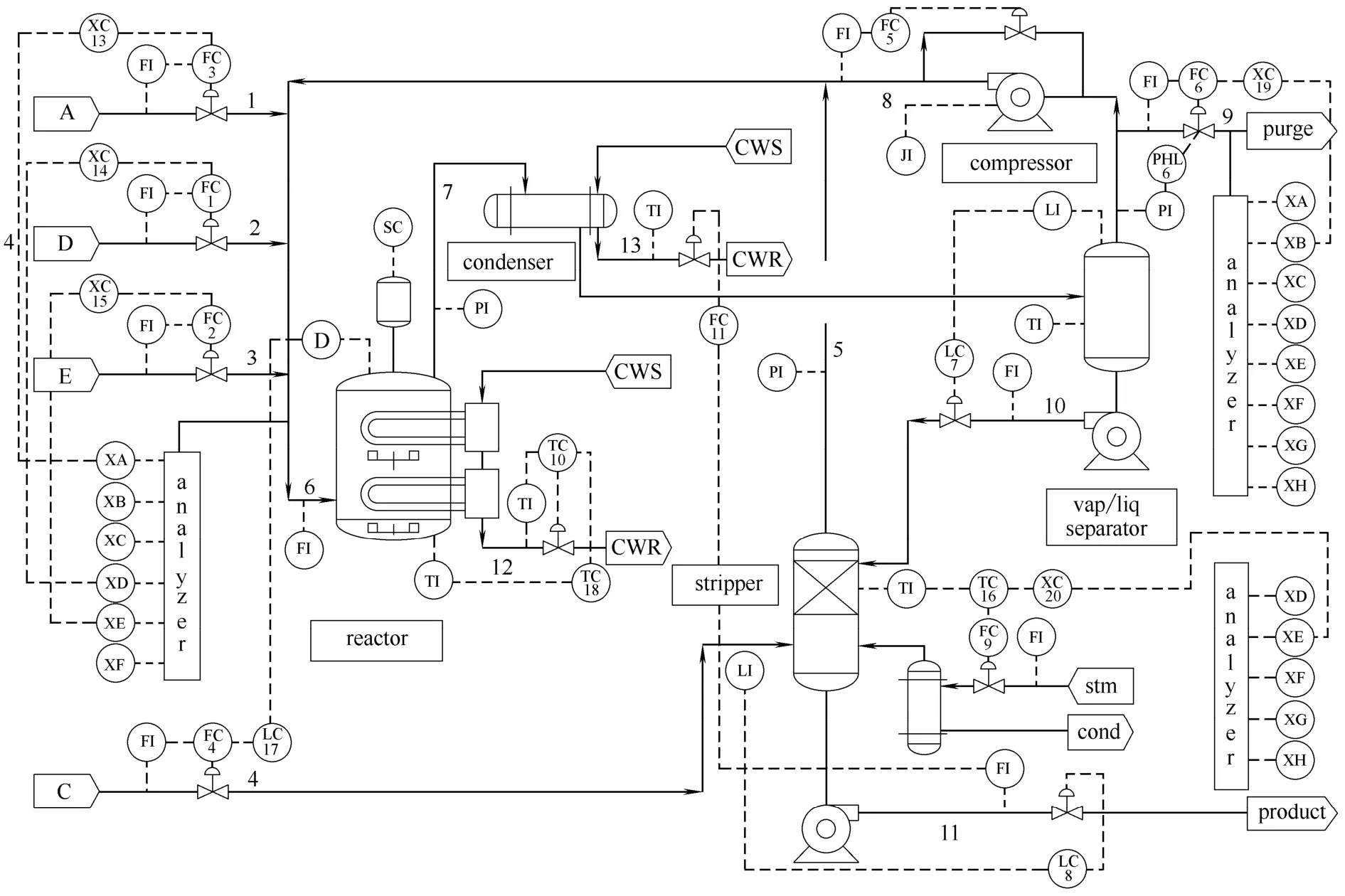
图1 TE过程结构Fig.1 Flowsheet of Tennessee Eastman process

首先，利用PCA和MIPCA方法对TE过程21种故障工况进行监测，并计算针对每种故障监测的故障漏报率，详情列于表1中。值得注意的是，故障3、9和15由于对过程的影响甚微，很多文献都证实这3种故障是很难被有效地检测出来的[7,23]。因此，在本文研究中不予考虑。在表1中，取得最小漏报率的监测指标已用黑体标出。显而易见，MIPCA方法在绝大多数故障类型上能取得优越于传统PCA方法的监测结果。尤其是针对故障5、10、16、19，故障漏报率得到大幅度的下降。虽然，MIPCA方法在故障13、17和18上的监测效果不如传统PCA方法优越，但是相应的漏报率相差微乎其微。为了更好地体现MIPCA相对于PCA方法的优越性，将故障5的过程监测图显示于图2中。很显然，传统PCA方法对故障5存在很大的漏报，而MIPCA方法能一直持续触发故障警报。

表1 TE过程故障漏报率Table 1 Fault missing alarm rates of TE process: PCAvsMIPCA/%

图2 故障5的过程监测结果Fig.2 Monitoring charts of fault 5

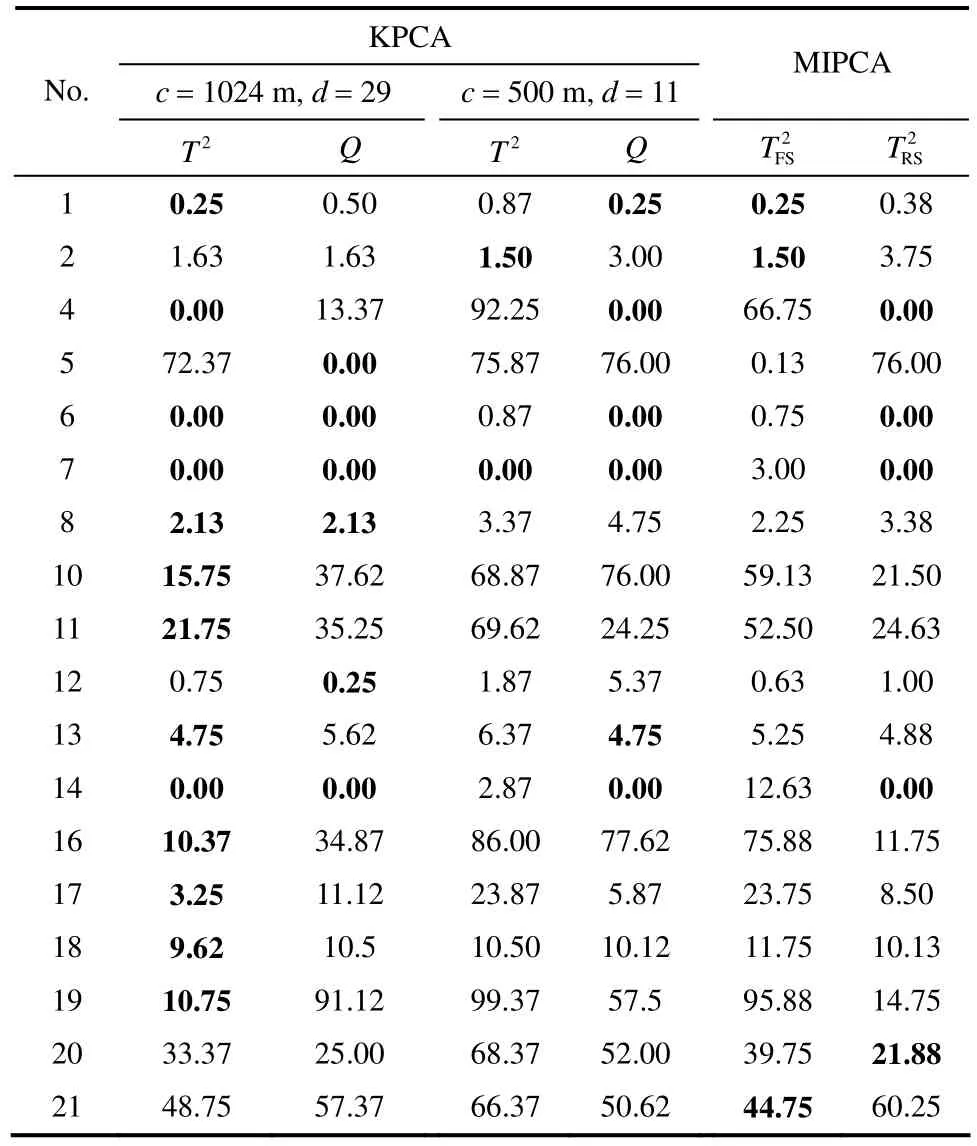
表2 TE过程故障漏报率Table 2 Fault missing alarm rates of TE process: KPCAvsMIPCA/%

其次，为了更进一步地验证MIPCA方法相比于KPCA方法的优越性，将它们对应的故障检测结果列于表2中。值得注意的是，由于KPCA模型建立时需人为确定对应核函数参数与潜隐变量个数，而前面已经提到核参数与潜隐变量的选择会对KPCA方法产生影响。因此，表中2所列的KPCA方法的监测结果分两组，分别对应文献[21]和[22]中的参数取值。从表2中可以发现，KPCA方法在c=1024 m，d=29这组参数取值下，在绝大多数故障类型上能取得优越于MIPCA方法的监测结果。但是，KPCA方法在另外一组参数取值条件下，故障检测效果远不如本文所提出的MIPCA方法。因此，KPCA方法的监测效果在一定程度上取决于参数的设定。若是没有充分的经验知识，实际应用中很难为之确定一组较好的参数值。可以说，相比于KPCA这种非线性的过程监测方法，本文的MIPCA方法仍具有一定的优越性。

在对比分析了MIPCA方法故障漏报效果后，还需继续验证MIPCA方法的故障误报率。通常来讲，较低的故障漏报率容易对应较高的故障误报率，也即将正常数据样本错误的判别为故障。利用另一组正常工况下采集到的500个数据，检验PCA和MIPCA各统计指标的误报率，对应结果如表3所示。从表中可以看出，MIPCA的故障误报率略低于PCA算法。通过表1～表3的对比分析，充分验证了基于MIPCA的过程监测方法的优越性和有效性。

表3 TE过程故障误报率Table 3 Fault false alarm rates of TE process/%

4 结 论

本文提出了一种基于MIPCA的统计过程监测方法。针对传统PCA模型求解过程中未充分考虑过程数据测量变量间的非线性相关性，在原有PCA方法的基础上，引入互信息定义数据的相关性矩阵。新的MIPCA方法不再局限于描述过程数据变量间的线性相关性，能为过程数据建立更确切的描述模型。在TE过程上的仿真研究也充分说明了MIPCA方法优越于传统PCA方法。然而，MIPCA仍旧是一种线性投影方法，如何把该方法扩展成非线性形式，对下一步的工作提出了挑战。此外，针对故障诊断的研究还需进一步的研究。

[1] Qin S J. Statistical process monitoring: basics and beyond [J].Journalof Chemometrics, 2003, 17 (7/8): 480-502.

[2] Ge Z, Song Z, Gao F. Review of recent research on data-based process monitoring [J].Industrial & Engineering Chemistry Research, 2013, 52 (10): 3543-3562.

[3] Qin S J. Survey on data-driven industrial process monitoring and diagnosis [J].Annual Reviews in Control, 2012, 36 (2): 220-234.

[4] Fan J, Wang Y. Fault detection and diagnosis of non-linear non-Gaussian dynamic processes using kernel dynamic independent component analysis [J].Information Sciences, 2014, 259: 369-379.

[5] Fan Xueli (范雪莉), Feng Haihong (冯海泓), Yuan Meng (原猛). PCA based on mutual information for feature selection [J].Control and Decision (控制与决策)，2013, 28 (6): 915-919.

[6] Lee J M, Yoo C K, Choi S W, Vanrolleghem P A, Lee I B. Nonlinear process monitoring using kernel principal component analysis [J].Chemical Engineering Science, 2004, 59 (1): 223-234.

[7] Tong C, Song Y, Yan X. Distributed statistical process monitoring based on four-subspace construction and Bayesian inference [J].Industrial & Engineering Chemistry Research, 2013, 52 (29): 9897-9907.

[8] Zhao C, Wang F, Zhang Y. Nonlinear process monitoring based on kernel dissimilarity analysis.Control Engineering Practice, 2009, 17 (1): 221-230.

[9] Li W. Mutual information functions versus correlation functions [J].Journal of Statistical Physics, 1990, 60 (5/6): 823-837.

[10] Kwak N, Choi C. Input feature selection for classification problems [J].IEEE Transactions on Neural Networks, 2002, 13 (1): 143-159.

[11] Han M, Ren W, Liu X. Joint mutual information-based input variable selection for multivariate time series modeling [J].Engineering Applications of Artificial Intelligence, 2015, 37: 250-257.

[12] Verron S, Tiplica T, Kobi A. Fault detection and identification with a new feature selection based on mutual information [J].Journal of Process Control, 2008, 18 (5):479-490.

[13] Jiang Q, Yan X. Plant-wide process monitoring based on mutual information-multiblock principal component analysis [J].ISATransactions, 2014, 53 (5): 1516-1527.

[14] Ge Zhiqiang (葛志强), Song Zhihuan (宋执环). PICA based process monitoring method [J].Journal of Chemical Industry and Engineering(China) (化工学报), 2008, 59 (7): 1665-1670.

[15] Downs J J, Vogel E F. A plant-wide industrial process control problem [J].Computers & Chemical Engineering, 1993, 17 (3): 245-255.

[16] Xie L, Lin X, Zeng J. Shrinking principal component analysis for enhanced process monitoring and fault isolation [J].Industrial & Engineering Chemistry Research, 2013, 52 (49): 17475-17486.

[17] MIToolbox for C and MATLAB. http://www.cs.man.ac.uk/~pococka4 /MIToolbox.html.

[18] Chiang L H, Russell E L, Braatz R D. Fault Detection and Diagnosis in Industrial Systems [M]. London: Springer-Verlag, 2001.

[19] Tong C, Palazoglu A, Yan X. Improved ICA for process monitoring based on ensemble learning and Bayesian inference [J].Chemometrics & Intelligent Laboratory Systems, 2014, 135: 141-149.

[20] Zhao Zhonggai (赵忠盖), Liu Fei (刘飞). Factor analysis and its application to process monitoring [J].Journal of Chemical Industry and Engineering(China) (化工学报), 2007, 58 (4): 970-974.

[21] Lee J M, Qin S J, Lee I B. Fault detection of non-linear processes using kernel independent component analysis[J].The Canadian Journal of Chemical Engineering, 2007, 85 (4), 526-536.

[22] Shao J D, Rong G, Lee J M. Generalized orthogonal locality preserving projections for nonlinear fault detection and diagnosis[J].Chemometrics & Intelligent Laboratory Systems, 2009, 96 (1): 75-83.

[23] Wang J, He Q P. Multivariate statistical process monitoring based on statistics pattern analysis [J].Industrial & Engineering Chemistry Research, 2010, 49 (17): 7858-7869.

Mutual information based PCA algorithm with application in process monitoring

TONG Chudong, SHI Xuhua
(Faculty of Electrical Engineering & Computer Science,Ningbo University,Ningbo315211,Zhejiang,China)

Principal component analysis (P monitoring CA) is a classical algorithm for feature extraction and has been widely used in multivariate statistical process. The essence of the PCA algorithm is to extract the correlation between process variables. However, the correlation matrix defined in the traditional PCA algorithm is limited to consider the linear relationship between variables, which cannot be employed to analyze the mutual dependence between two measured variables. With recognition of this lack, a novel mutual information based PCA (MIPCA) method is proposed for process monitoring. Distinct from the traditional PCA, MIPCA defines the relationship between variables by calculating the mutual information, and the original correlation matrix is replaced by the resulting mutual information matrix. The eigenvectors of the mutual information matrix can thus be utilized as the directions of feature extraction. On the basis of MIPCA, a statistical process monitoring model can then be constructed. Finally, the feasibility and effectiveness of the MIPCA-based monitoring method are validated by a well-known chemical process.

principal component analysis; numerical analysis; process systems; mutual information; fault detection; statistical process monitoring

SHI Xuhua, shixuhua@nbu.edu.cn

10.11949/j.issn.0438-1157.20150374

TP 277

：A

：0438—1157（2015）10—4101—06

2015-03-23收到初稿，2015-05-29收到修改稿。

联系人：史旭华。

：童楚东（1988—），男，博士，讲师。

浙江省自然科学基金项目（LY14F030004）；浙江省科技厅公益项目（2015C31017）。

Received date: 2015-03-23.

Foundation item: supported by the Natural Science Foundation of Zhejiang Province, China (LY14F030004).