GM（1,1）预测模型在产品销售预测中的运用

江玉杰

（三江学院商学院，江苏南京210000）

GM（1,1）预测模型在产品销售预测中的运用

江玉杰

（三江学院商学院，江苏南京210000）

企业要想在同质化市场上提高竞争力，必须及时地预测产品销量，以便快速应对市场变化。基于灰色系统理论的GM（1,1）预测模型具有对数据要求限制少、预测精度高等特性，特别适合产品销量的预测。本文以FM公司矿泉水为例，详细地阐述G(1,1)预测销售量的全过程，这对相关人士具有重要的参考价值。

GM（1,1）预测模型；销售量预测；模型函数；精度检验

当今社会，消费者的需求日益呈现个性化、多样化、特殊化，使得同质化市场的竞争更加激烈。因此，企业要想在同质化市场上增强产品竞争力，在提高产品质量、改进产品包装以及完善售后服务的同时，必须及时地把握市场变化，以便合理的规划有限的人力、物力、财力，进而提高企业的核心竞争力。而销售预测是这一过程中重要的环节。销售预测是指预测者根据以往的销售情况以及所采用的预测模型对未来销售情况所做的预测。其目的是通过销售预测，实现以销定产、及时生产，降低交货提前期、产品库存率，提高交货能力、服务水平。

基于灰色系统理论的GM（1,1）预测模型是通过对原始时间序列进行累加生成能够把原先时间序列不显著的变化趋势转变为具有显著的变化趋势，从而挖掘出时间序列的内在规律，然后建立预测模型，最后通过累减还原进行预测。现如今GM（1,1）预测模型在经济管理、环境科学、工农业生产、图像信息、航空航天等领域得到了广泛的运用，解决了许多过去难以解决的实际问题，展示了极为广泛的应用前景。

本文运用GM（1,1）预测模型详细地阐述预测FM公司矿泉水未来年度销售量的全过程，为初学者、预测者、决策者深入地理解G(1,1)预测模型原理具有重要的参考价值。

1 GM（1,1）预测模型概述

在GM（1,1）预测模型中，G是Grey缩写，表示灰色；M是Model的缩写，表示模型；（1,1）分别表示1阶方程、1个变量。通常，GM（1,1）预测模型适用于时间序列无明显趋势，通过累加的方式可生成有明显趋势的时间序列情形。

设 原 始 时 间 序 列 x（0）=｛x（0）（1）,x（0）（2）,…x（0）（n）｝，其 1 次 累 加 生 成 序 列 为其中

由于新生成序列x（1）一般近似地服从指数规律，GM（1,1）预测模型的白化形式的一阶常微方程为：

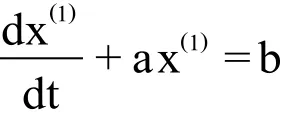
式中：a称为发展灰数，b称为内生控制灰数，a、b均为待估参数。对于待估参数a、b，可采用最小二乘法求解，其估计值为：

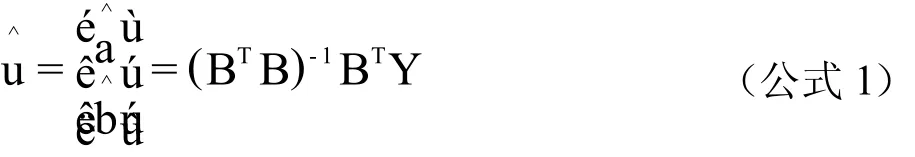
其中，数据矩阵B、数据向量Y由下面公式确定：

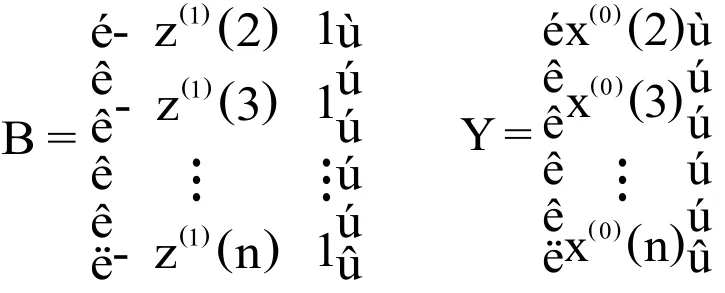
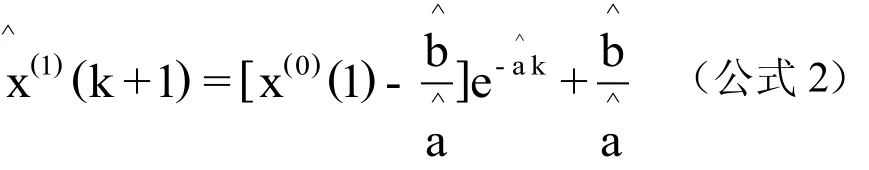
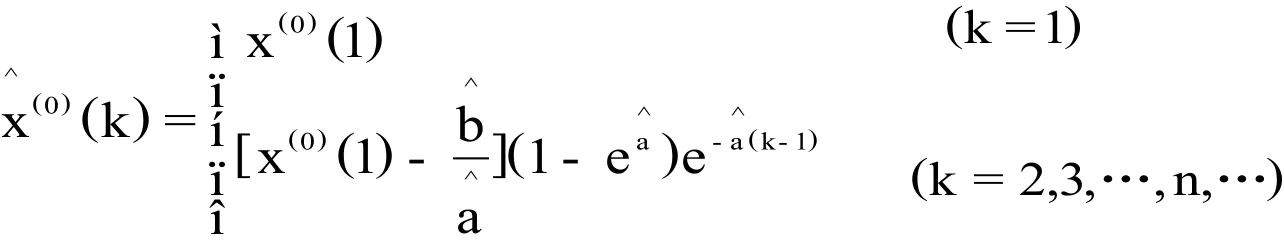
2 矿泉水年度销售量预测

表1第3列所示数据是FM公司矿泉水近8年来的年度销售量。该公司预测者需要根据近8年的数据，预测出2015年、2016年的年度销售量，以便及时地应对矿泉水市场的变化、改进矿泉水市场营销策略。

通常，运用 G(1,1)预测模型建立预测函数时，需要进行以下步骤：①数据检验与处理；②建立模型函数；③精度检验及预测。

2.1 数据的检验与处理

为了保证 GM（1,1）建模的可行性，首先需要对已知数据进行级比检验。设原始时间序列x（0）=｛x（0）（1）,x（0）（2）,…x（0）（n）｝，则计算序列的级比公式为：

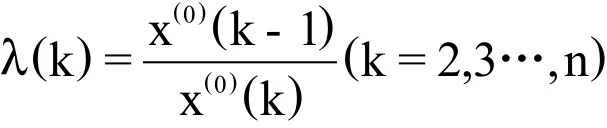
根据表1第3列数据，可建立建立原始时间序列x（0），其表达式为：

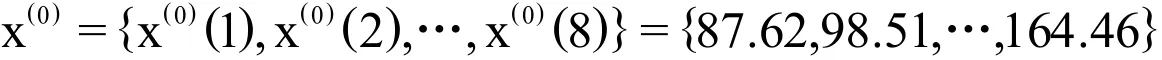
2.2 建立模型函数

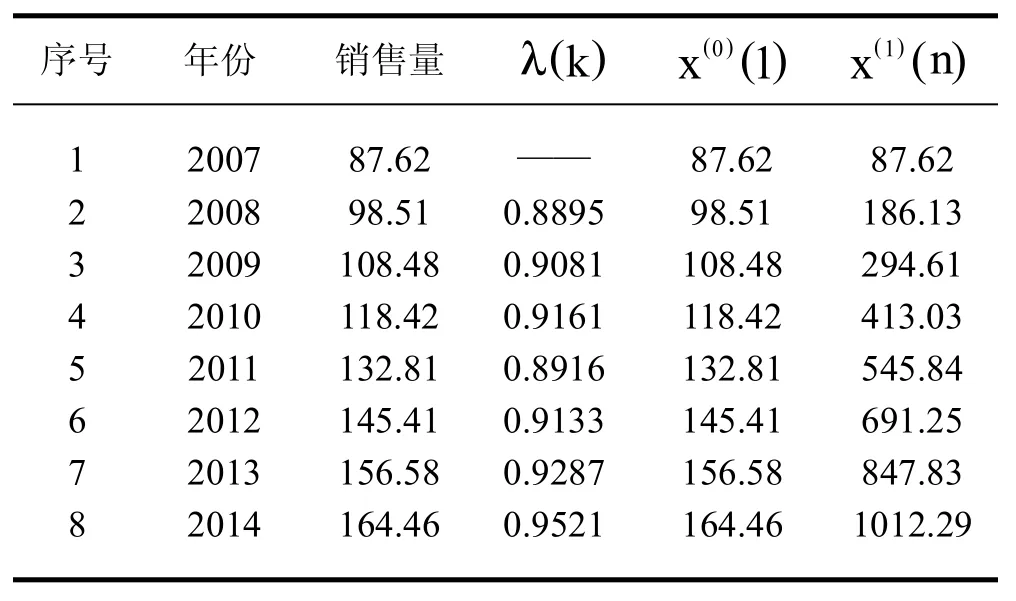
表1 FM公司矿泉水历年销售量单位：百万瓶

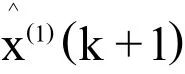
在构建GM（1,1）时，需要采用累加方式对原始数据进行生成处理，使生成序列变成有规律的序列。累加方式就是通过序列间各时刻数据的依次累加得到新的数据与序列。累加前的序列称为原始序列，累加后的序列称为生成序列。根据表1第3列数据，可得到基于FM矿泉水年销售量的生成序列x（1），其表达式为：

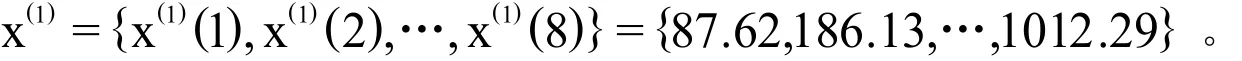
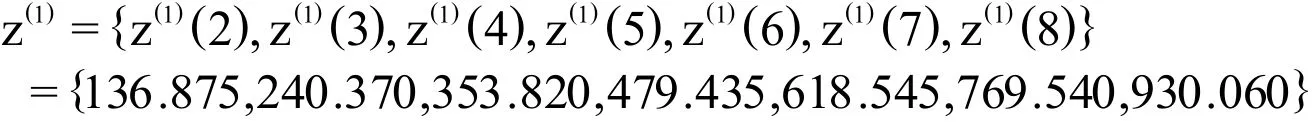
运用最小二乘法求解待估参数a、b。将数据矩阵B、数据向量Y计算值代入公式一，可就得待估参数向量：

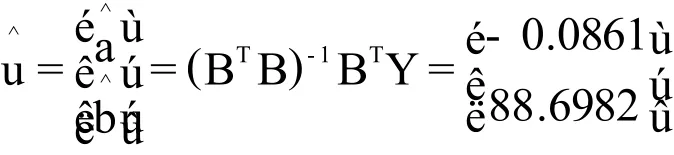
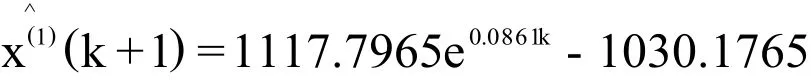
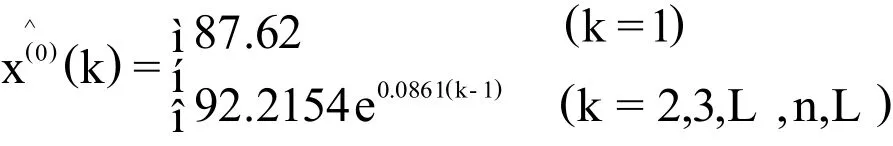
2.3 精度检验及预测

2.3.1 精度检验

产品销量预测就是借助于过去的数据去推断、预测未来的销售量。基于灰色理论的 G(1,1)预测模型就是通过原始数据的处理和灰色模型的建立，发现、掌握系统发展规律，对系统未来状态做出相对客观的定量预测。因此，在建立起模型函数之后，必须检验模型函数的可信程度，根据需要进行必要的修正。在模型函数精度未达到一定标准前，不可进行实际销量预测。

一般地，当∣a∣≤2时，G(1,1)预测模型有意义。但随着a的取值不同，模型预测效果也不同。通常，当-0.3≤a≤2时，GM（1,1）预测模型可用于中长期预测；当-0.5≤a＜-0.3时，GM（1,1）预测模型可用于短期预测，中长期预测慎用；当-0.8≤a＜0.5时，用 GM（1,1）预测模型做短期预测应十分谨慎；当-1≤a＜-0.8时，应采用残差修正GM（1,1）预测模型；当-2≤a＜-1时，不宜采用GM（1,1）预测模型。根据前文可知，FM公司矿泉水近8年销售量的预测模型函数中a为-0.0861，使得所建模型可用于中长期预测。

通常，检验灰色 G(1,1)预测模型的精度的方法有4种，即残差检验、关联度检验、级比偏差检验以及后验差检验，而一般以残差检验和后验差检验应用最为普遍。所以，本文针对FM公司矿泉水销量所建的预测模型函数采用残差检验、后验差检验两种方法检验其精度。

残差检验就是以相对误差占观察值的比例大小来衡量模型函数的好坏，通常以相对残差指标来反映模型函数的预测精度。如果预测值与观察值之间的误差较大，则不能以此模型进行预测，必须采用一定方式来提高模型函数精度。相对残差计算公式：

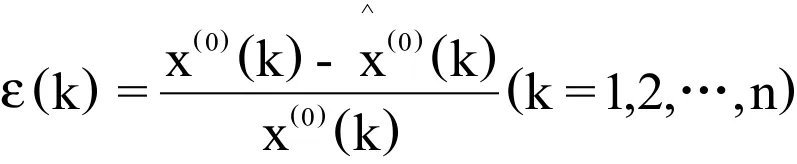
后验差检验法是按照后验差比值C、小误差概率P两个指标来评定模型精度等级。其等级标准如表3所示。后验差比值C越小，则说明残差序列方差小，原始序列数据方差大，此时残差集中度高，摆动幅度小；小误差概率P越大，则说明残差与残差算术平均数的绝对值小于给定值的点较多，所以C值越小、P值越大，其模型函数预测精度就越高。如果后验差检验发现 GM（1,1）模型预测精度等级为不合格，那么可以进行残差修正的GM（1,1）模型。

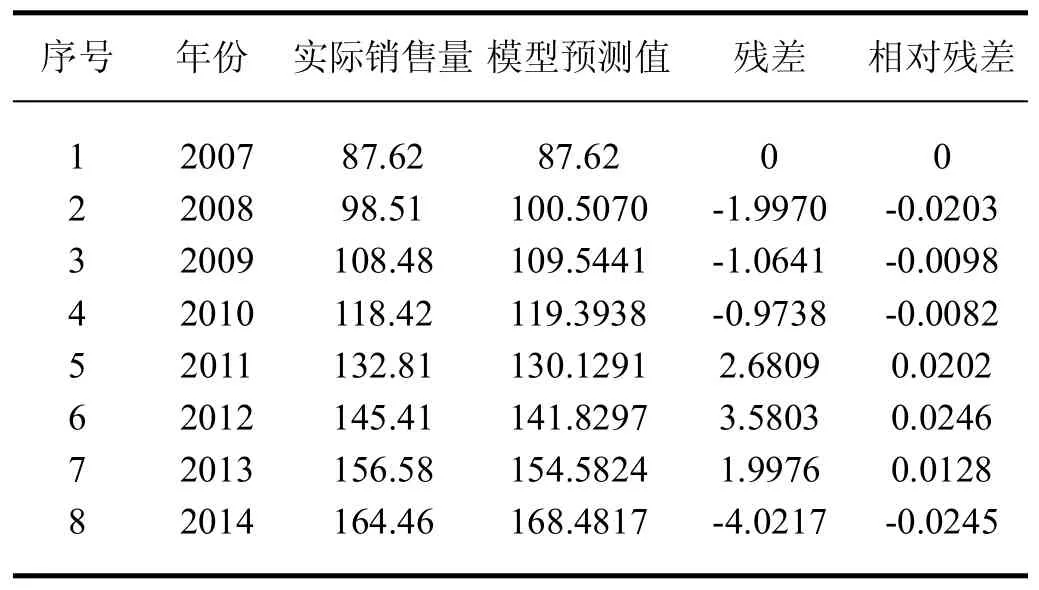
表2 残差检验精度表

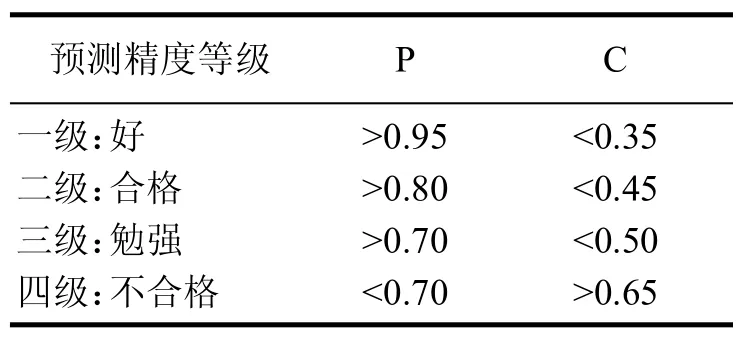
表3 预测精度等级表

计算后验差比值C、小误差概率P两个指标的步骤如下：

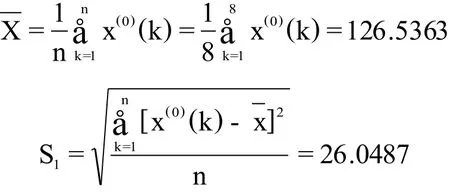
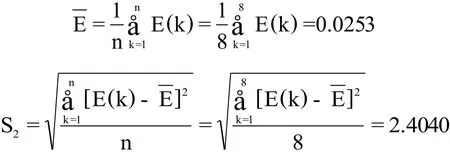
第三步：计算后验差比值C、小误差概率P

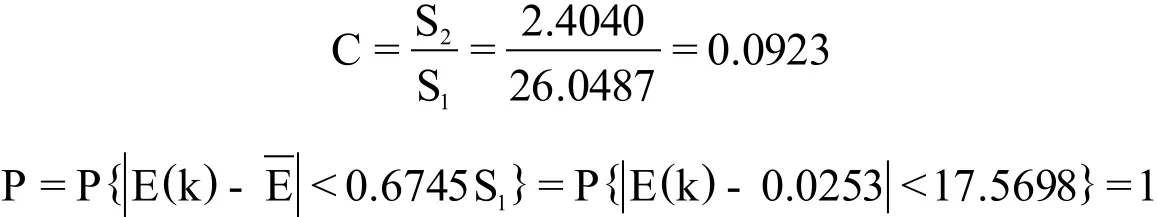
显然，根据计算结果可知，后验差比值C、小误差概率P满足预测精度一级标准：P＞0.95、C＜0.35。因此可以认为所建G(1,1)预测模型函数预测力强。

2.3.2 预测销售量

基于模型函数通过精度检验，所建模型函数可用于外推预测。分别将k=9、k=10代入所建G（1,1）预测模型函数：

3 结论

灰色理论是以“部分信息已知、部分信息未知”的小样本、“贫信息”为研究对象，通过对部分已知信息的挖掘，提取有价值的信息，实现对研究对象发展规律的正确的把握。而GM（1,1）预测模型是灰色预测理论中最为核心的部分。由研究所建立的 GM（1,1）预测模型函数可知，FM公司矿泉水销售量在中长期内还会保证相对稳定的增长速度。这样预测结论对于FM公司的长期规划具有重要的参考价值。

[1]陈华友.组合预测方法有效性理论及其应用[M].北京:科学出版社，2008:28-32.

[2]李家会.灰色预测模型在产品销售预测中的应用[J].科技信息，2014(11)：93-94.

[3]段锋,杨芬.灰色预测模型的研究及应用[J].湘南学院学报，2008(02)：17-20

（责任编辑：田犇）

On the Application of GM (1,1)Prediction Model in Product Sales

JIANG Yu-jie
(Business School,Sanjiang University,Nanjing Jiangsu 210000,China)

F272.1

B

1674-2346(2015)02-0036-06

2015－01－30

江玉杰，男。研究方向：市场营销（物流管理）

10.3969/j.issn.1674-2346.2015.02.008