利用测高重力异常建立南中国海海底地形模型

欧阳明达 孙中苗 翟振和 刘晓刚

1 信息工程大学地理空间信息学院，郑州市科学大道62号，450001

2 西安测绘研究所，西安市雁塔路中段1号，710054

3 地理信息工程国家重点实验室，西安市雁塔路中段1号，710054

4 西安测绘信息技术总站，西安市西影路36号，710054

海洋卫星雷达测高技术的出现，使海底地形测量技术得到飞速发展［1－3］。利用测高重力异常反演海底地形主要包括两类方法：解析法和统计法［2，4］。解析法基于Parker理论和板块模型，利用响应函数反演海底地形［5－9］。统计法最早由Tscherning提出，将重力数据进行统计迭代，改善了已有的水深模型［10］。此后，翟国君等［11］也使用类似方法开展了地形反演研究。2008年，美国地球物理中心（NGDC）发布1′分辨率的ETOPO1海深模型［12］。2011年，丹麦国家空间中心（DNSC）发布1′分辨率的重力数值模型DTU10GRAV，其残差的均值为0.39mGal，标准差为3.82mGal，最大值为36.89mGal［13］。本文利用DTU10GRAV 海洋重力异常模型和ETOPO1海底地形模型，采用解析法反演南中国海1′×1′的海底地形，并利用ETOPO1海底地形模型和实测检核点水深对其精度进行评价。

1 海深反演的基本原理

Parker将引力位引入到频率域，给出地下物质界面起伏所产生的重力异常的频率域表达式［14］：

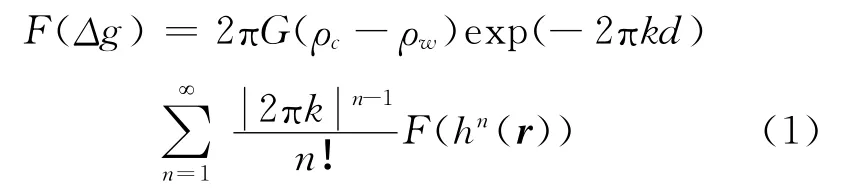
式中，G为地球引力常数；ρc为海底洋壳密度；ρw为海水密度；k＝（kx，ky）＝（1／λx，1／λy），其中，（kx，ky）和（λx，λy）为x和y方向的频率和波长；F为傅里叶变换；d为平均海深；，为圆频率。

当海底地形负荷的波长小于地壳的弹性厚度时，式（1）中的第一项起主要作用，它仅取决于平均海深。此时，重力异常和海底地形之间是线性关系［15］：

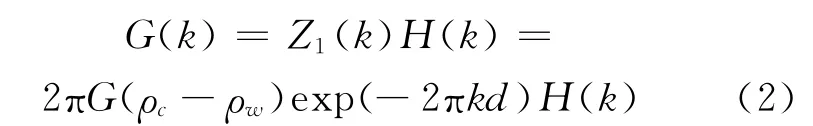
G（k）和H（k）分别为重力异常和水深的傅里叶变换，Z1（k）为响应函数。

Z1（k）中的2πG（ρc－ρw）是布格常数，exp（－2πkd是向上延拓（从海底到海面）。将上式逆变换，可以通过卫星测高重力异常计算海底地形。在频率域，该模型如下：

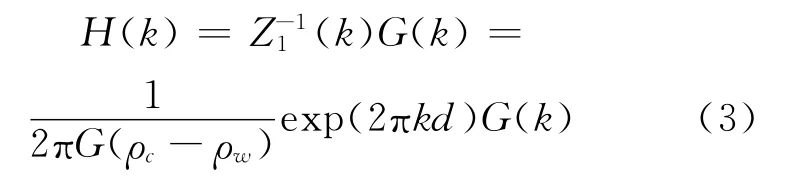
上式为未考虑补偿模型的响应函数关系式。当海底地形负荷波长大于海底洋壳弹性厚度时，需要顾及Airy补偿模型。这时的响应函数需要顾及两个层面，一个为平均海深，另一个为补偿深度，响应函数表达式为［15］：

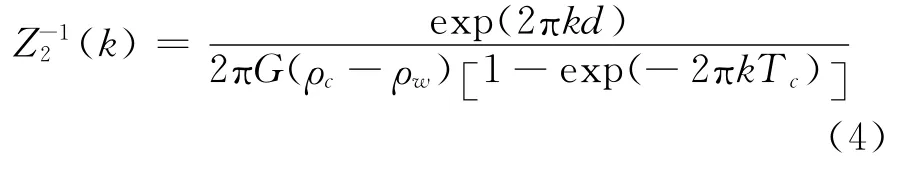
Tc为平均地壳厚度，其他参数含义同上。顾及挠曲补偿模型的响应函数表达式为［16］：

式中，ρi为挠曲内填补物质的密度，ρ2、ρ3为上、下地壳层密度，ρm为地幔层密度，T2、T3为上、下地壳层厚度。φ（k）表达式如下：

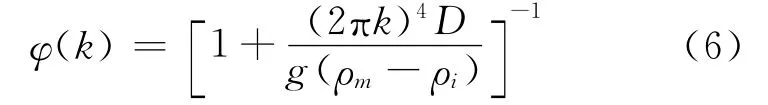
D为岩石圈的挠曲刚度，它与岩石圈的有效弹性厚度Te有关：

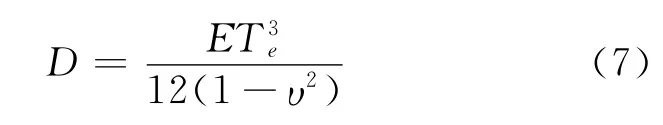
υ为岩石圈的泊松比，E为弹性模量。

从式（3）～（5）可以看出，重力异常与海水深度的响应函数和地幔密度、海底洋壳密度、地壳密度、地壳厚度、岩石圈挠曲刚度和有效弹性厚度相关。

2 响应函数

频率域内重力异常和海底地形之间的关系通过响应函数Z（k）建立，它具有线性、各向同性等性质。利用式（3）～（5）的逆变换计算响应函数理论值，其所采用的地球物理参数见表1。图1 分别为未补偿模型、Airy补偿模型、挠曲补偿模型的响应函数分别受平均海水深度d、平均地壳厚度Tc和岩石圈有效弹性厚度Te影响所发生的变化。可以看出，重力异常和海底地形的关系是非线性的，但是在波段10～110km 范围内呈近似的线性关系。在小于110km 的波长范围，d对未补偿响应函数模型的影响是不同的。对Airy补偿和挠曲补偿响应函数模型而言，其形态基本相同。在大于110km 的波长范围，响应函数不仅依赖于d，Tc、Te都会对其造成很大影响。因而，当采用响应函数建立两者关系，实现海底地形反演时，获知精确的地球物理参数十分必要，这些地球物理参数可以参阅相关文献或根据诸如Crust2.0等全球地壳模型等获取。

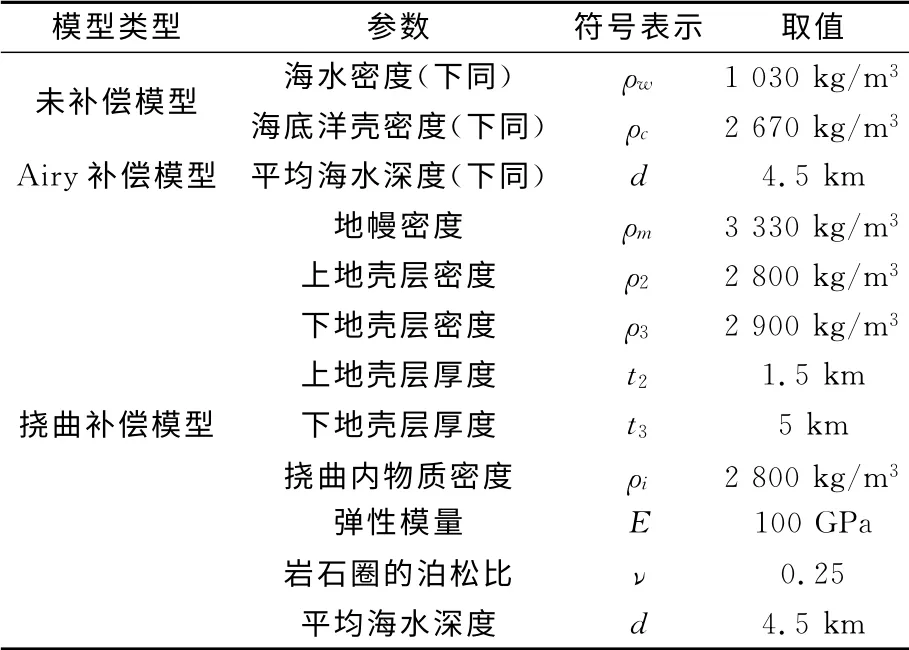
表1 响应函数中假设的地球物理参数Tab.1 Summary of parameters assumed in the gravity modeling and bathymetry prediction

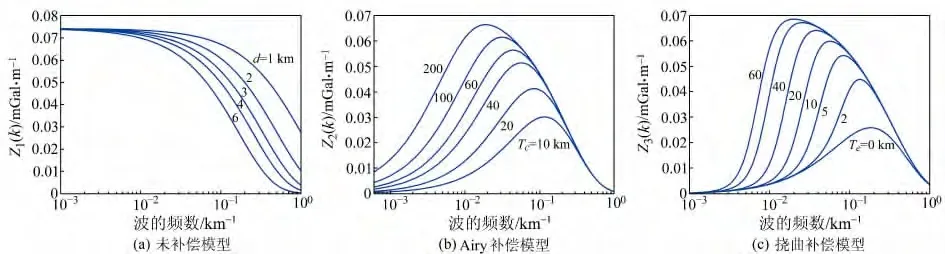
图1 响应函数值Fig.1 Value of response function

3 实验结果与分析

3.1 数据准备和前期处理

研究范围位于南中国海112°～119°E、12°～20°N。作为检核的船测水深数据来自美国地球物理中心（NGDC）网站，共计10 529 个，如图2所示。其背景为ETOPO1海深模型，黄色点为检核点，红色和绿色点为用作检核的Cruise＿01 和Cruise＿02船测轨迹。测高重力异常数据（分辨率为1′）来自丹麦科技大学空间中心，如图3所示。

3.2 处理流程

顾及Airy补偿和挠曲补偿的响应函数模型涉及物理参数众多，过程复杂，将另文给出。以下仅采用较简单的未补偿响应函数模型对海底地形在15～110km 的中高频分量进行反演。根据文献［2］，密度差异常数Δρ确定为1 640kg／m3，采用移去－恢复法进行海底地形反演。

1）采用110km 的高斯函数对初始重力异常进行低通滤波，获得参考重力异常。将参考重力异常从初始异常值中移去，得到残余重力异常。高斯函数进行滤波，获得参考海深模型，其均值即为平均海深d。

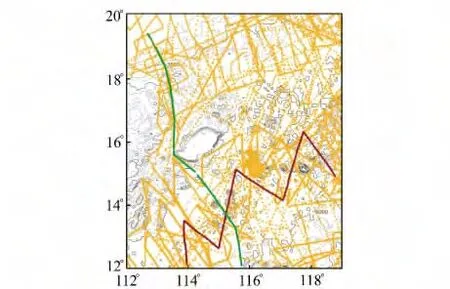
图2 船测航迹分布Fig.2 Distribution of shipborne tracks

2）对该海域的ETOPO1海深模型也采用该

3）将残余重力异常通过未补偿响应函数模型进行反演计算，得到残余海深。该残余海深和参考海深模型之和即为南中国海海深模型。

值得注意的是，由于响应函数中存在exp（2πkd）项，该项为向下延拓，会带来很大的高频噪声。根据文献［5］，选用波长为15km 的高斯滤波函数进行抑制，得到最终的海深模型。由图4可以看出，大部分海域内两模型符合较好，但在海岛附近以及多海山地区两者差异较大，说明反演模型在该部分海域内的精度不甚理想。

图3 测高自由空间重力异常Fig.3 Altimetry－derived gravity anomalies

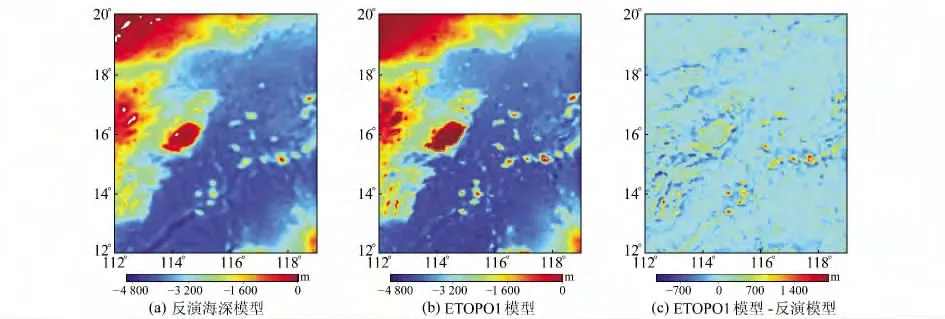
图4 南中国海海底地形模型及其比较Fig.4 Bathymetry models in the South Sea and differences of this two

3.3 精度评价

用反演模型插值计算得到检核点处水深，并与实测值比较获得其残差。残差主要集中在0～200m 范围，部分残差过大的予以剔除。处理后的残差和相对精度指标见表2。表2同时示出了ETOPO1模型在该海域的精度统计信息。可以看出，本文反演模型的相对精度保持在10%左右，精度水平略低于ETOPO1模型。

图5示出了残差、相对精度与水深和重力异常的关系。在深水区，残差和相对精度的数值较小，较大数值大多出现在－2 500～0 m 的水域。残差、相对精度与重力异常的相关性不太明显，但总的来说，深水海域、低异常值区间的反演精度明显好于浅水海域以及高重力异常值区间。

表3给出了残差、相对精度在不同水深层的量化结果。在－3 000m 以下海域的大多数残差值位于0～170 m 区间，相对精度保持在5%以内；在－3 000m 以上海域，残差值和相对精度出现大的突变。结合图4可知，该水深层以上多分布有海山和大陆架，量化显示结果与§3.2结论一致。

表2 残差、相对精度结果统计Tab.2 Statistics of the differences and relative precision

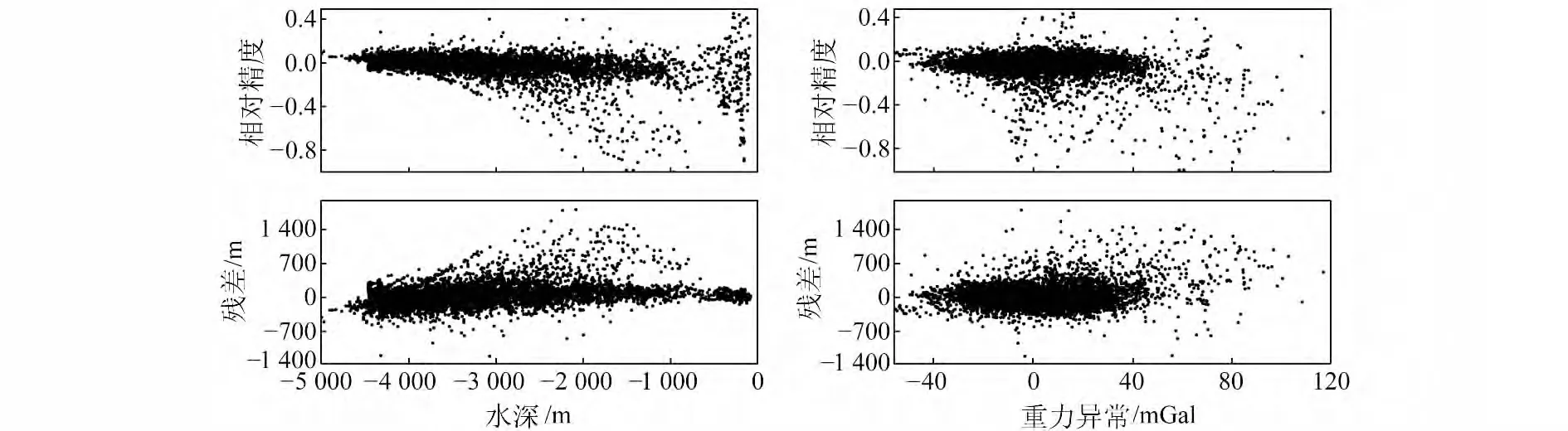
图5 残差、相对精度与水深和重力异常的关系Fig.5 The relationship between the differences，relative precision and the bathymetry and gravity anomaly

表3 不同水深区间的残差、相对精度结果统计Tab.3 Statistics of the differences and relative precision in different intervals of deep

图6为Cruise＿01和Cruise＿02船测航迹测深剖面比较，实线为实测水深，点线为反演模型插值水深，两者走势基本一致，但在海山处插值水深往往低于实测水深，且出现较大的残差量级。反演海深模型过低估计了海山峰值，不能被水下潜器用于导航。

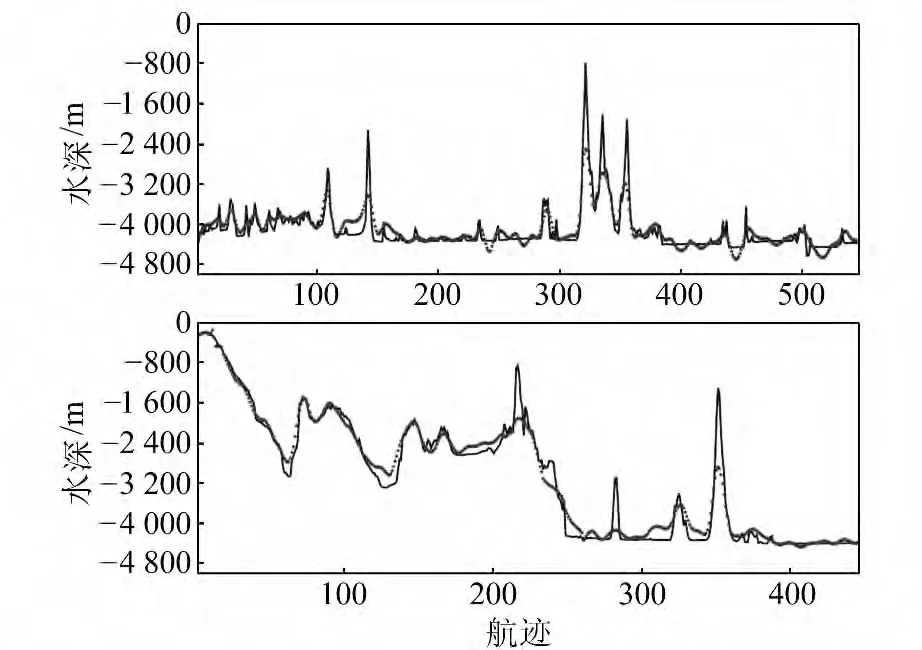
图6 Cruise＿01和Cruise＿02航迹比较Fig.6 Comparisons for bathymetry along the cruise＿01and cruise＿02

4 结 语

本文采用解析法反演了南中国海在中短波范围的1′×1′海底地形，反演模型的相对精度为10%左右，略低于ETOPO1模型，在多海山地区以及大陆架覆盖海域精度稍差，且存在过低估计海山峰值的问题。在后续研究中，可以尝试通过最小二乘配置方法对其作进一步改善。

［1］黄谟涛，翟国君，管峥，等.海洋重力场测定及其应用［M］.北京：测绘出版社，2005（Huang Motao，Zhai Guojun，Guan Zheng，et al.The Marine Gravity Field Determination and Its Application［M］.Beijing：Surveying and Mapping Press，2005）

［2］王勇，许厚泽，詹金刚.中国海及其邻近海域高分辨率海底地形［J］.科学通报，2001，46（11）：956－960（Wang Yong，Xu Houze，Zhan Jingang.High Resolution Sea Floor Topography of China Sea and Its Adjacent Areas［J］.Chinese Science Bulletin，2001，46（11）：956－960）

［3］Neumann G A，Forsyth D W，Sandwell D.Comparison of Marine Gravity from Shipboard and High－density Satellite Altimetry Along the Mid－Atlantic Ridge［J］.J Geophys Res，1993，20：1 639－1 642

［4］黄谟涛，翟国君.利用卫星测高资料反演海底地形研究［J］.武汉大学学报：信息科学版，2002，27（2）：133－137（Huang Motao，Zhai Guojun.The Recovery of Bathymetry from Altimeter Data［J］.Geomatics and Information Science of Wuhan University，2002，27（2）：133－137）

［5］李大炜，李建成，丰海，等.利用卫星测高数据反演中国海及邻近海域海底地形［J］.大地测量与地球动力学，2009，29（4）：70－73（Li Dawei，Li Jiancheng，Feng Hai，et al.Research on Inversion of Seafloor Topography of China Sea and Its Adjacent Areas from Satellite Altimetric Data［J］.Journal of Geodesy and Geodynamics，2009，29（4）：70－73）

［6］方剑，张赤军.中国海及邻近海域2′×2′海底地形［J］.武汉大学学报：信息科学版，2003，28（1）：38－40（Fang Jian，Zhang Chijun.2′×2′Sea Floor Bathymetry Prediction of China Sea and Its Vicinity［J］.Geomatics and Information Science of Wuhan University，2003，28（1）：38－40

［7］罗佳.由测高数据和海洋重力资料联合反演海底地形［D］.武汉：武汉大学，2000（Luo Jia.Bathymetry Inversion Combining Satellite Altimetry and Marine Gravity Data［D］.Wuhan：Wuhan University，2000

［8］聂琳娟，吴云孙，金涛勇，等.基于海水质量亏损引起的重力异常反演南海海底地形［J］.大地测量与地球动力学，2012，32（1）：43－46（Nie Linjuan，Wu Yunsun，Jin Taoyong，et al.Inversion of Submarine Topography of South China Sea by Using Gravity Anomaly Caused by Mass Deficiency［J］.Journal of Geodesy and Geodynamics，2012，32（1）：43－46）

［9］Watts A B，Sandwell D T，Smith W H F，et al.Global Gravity，Bathymetry，and the Distribution of Submarine Volcanism Through Space and Time［J］.J Geophys Res，2006，111：B08408

［10］Tscherning C C，Knudsen P，Foesberg R.First Experiments with Improvement of Depth Information Using Gravity Anomalies in the Mwditerranean Sea［R］.University of Thessaloniki，1994

［11］Zhai Guojun，Huang Motao，Ouyang Yongzhong，et al.A Modified Method for Recovering Bathymetry from Altimeter Data［J］.International Association of Geodesy Symposia，2003，126：84－88

［12］Amante C，Eakins B W.ETOPO1 1Arc－minute Global Relief Model：Procedures，Data Sources and Analysis［R］.NOAA Technical Memorandum，2009

［13］Baltazar O，Knudsen A P.The DNSC08GRA Global Marine Gravity Field from Double Retracked Satellite Altimetry［J］.Journal of Geodesy，2010，84：191－199

［14］Parker R L.The Rapid Calculation of Potential Anonmalies［J］.J Geophys Res，1972，31：447－455

［15］Watts A B.An Analysis of Isostasy in the World’s Oceans：1 Hawaiian Emperor Seament Chain［J］.J Geophys Res，1978，83：5 989－6 004

［16］Watts A B.Isostasy and Flexure of the Lithosphere［M］.New York：Cambridge University Press，2001