中国及其邻区地形和均衡重力梯度的球面计算

叶周润 柳林涛 梁星辉

1 中国科学院大学，北京市石景山区玉泉路甲19号，100049

2 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室，武汉市徐东大街340号，430077

地形和均衡影响的计算是非常重要的数据处理技术［1－5］。在忽略离心力的微小影响假设下，地形改正通常通过计算正演模型引力位的相关导数来实现。一般而言，在局部范围内常选用直角坐标系下的棱柱体模型，其引力位及其相关导数都有严格的理论表达式，同时对应的谱域形式通常采用FFT技术［6－9］。由于地球形状接近球体，球坐标下的近似模型可以尽量避免平面误差从而比较满足研究实际。在空间域，卡尔斯鲁厄理工学院的研究团队发展了一套基于Tessroid 单元体的泰勒展开方法［10－12］。在三维频谱域，常采用基于单层位技术的球谐分析方法［13－14］。对于均衡影响计算，理论上是压力平衡原理下地形的补偿影响，在计算方法上和地形正演没有实质差异［11］。

重力梯度是重力位的二阶导数，能从多角度反映异常体的中心点和边界等细节信息［15］。最新的GOCE模型改进了165～220阶的地球重力场细节，可以捕捉更多的地球内部信号［16］。本文计算了中国及其邻区地形和均衡的重力梯度影响，并给出均衡重力梯度异常分布图。实验中原始重力梯度数据来自GOCO03S位系数模型，且保留了高阶GOCE中的高频数据［17］。在地形改正部分，原始数据来自DTM2006高程模型［18－19］。在均衡模型选取方面，以Airy－Heiskanen均衡模型起主导作用［3］。

1 计算方法介绍

1.1 由GOCE模型计算扰动重力梯度值

解算完成的GOCE 模型最终以球谐位系数形式发布。如果要得到全球或局部地区的扰动重力梯度值，则需要通过球谐综合方法。其扰动位合成的数学基本表达式如下：

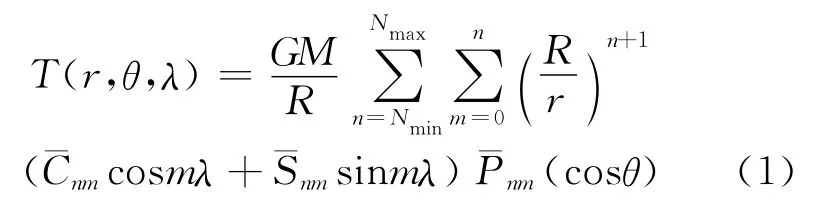
这里，r、θ和λ分别表示计算点的球心距离、纬度和经度；GM代表地球总质量和万有引力常数的乘积；R是地球平均半径和表示扰动位系数；是完全正则化的缔合勒让德函数；Nmin和Nmax分别为扰动位球谐表达的起始和最大阶数，考虑到GOCE模型的最大阶次，Nmin和Nmax取值为2 和250。

因为所有计算量是扰动位在纬度、经度及地心方向的二阶导数，则［17］：

具体表达式如下：

式中的相关表达式详见文献［9］。

1.2 球谐谱正演扰动重力梯度

在大地水准面为球面的假设下，地形单层位3次项球谐谱引力位展开式在形式上和式（1）一致［13］，但为了表达方便，我们定义：

在具体计算中，式（1）中的球谐系数由下式代替：

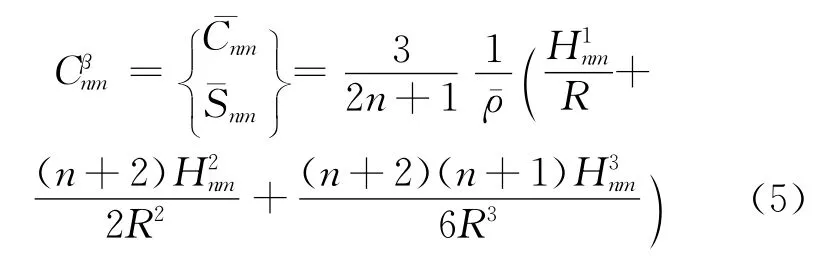
其中，

这里，i∈｛1 ，2，3｝ ；表示地球平均密度，取值5 500 kg／m3；h2和h1分别表示积分体的高程上下限，具体数值以球面（大地水准面）为基准，球面以上为正，反之为负（图1）。这里注意：1）球谐阶次n起始项为0。考虑到地形信号和和重力模型分辨率的匹配，n最大项截至250。2）从地形扰动位计算各重力梯度分量，可直接采用式（3）。

图1 地形示意图Fig.1 Schematic view of topography

1.3 Airy－Heiskanen均衡模型

如图2，在Airy－Heiskanen（A－H）模型中，地壳漂浮在较重的均质岩浆上，较轻的山根补偿山体的质量过剩，较重的反山根补偿海水的质量不足。一般设定地球正常地壳深度D＝30km，补偿物质和地幔物质密度差为600kg／m3。

如果假定大地水准面为近似球面，根据等质量原则，则（反）山根公式表述如下［11］：这里ρ0和ρw分别为岩石和海水密度，取值2 670 kg／m3和1 025kg／m3。

图2 Airy－Heiskanen均衡模型Fig.2 Isostatic model of Airy－Heiskanen

2 实验及结果分析

实验区域为纬度0°～59°、经度60°～149°的中国及其邻近区域，最终图形结果均以1°×1°分辨率展示。实验中，球谐合成时的正常重力场模型为GRS80，所有计算参考高度为GOCE轨道平均高度255km。此外，由于空气的重力梯度效应微小，作忽略处理［14］。

GOCO03S模型恢复得到的255km 中国及其邻近区域上空的扰动重力梯度分布见图3，其统计结果见表1。从图可见，纬度方向的扰动梯度在中国范围内主要集中在青藏高原及其邻区，表现为高原区域为负、两侧为正的近似对称异常分布。较于前者，经度方向的重力梯度异常信息更加丰富，在经度90°～110°范围和太平洋区域内存在显著的竖向梯度异常带；在球心方向的垂直梯度图中，青藏高原和新疆地区图形轮廓类似于纬度方向但数值正负相反，且在日本和太平洋地区异常图形与环太平地震带高度吻合。

图4是基于图3数据经过地形改正后的扰动重力梯度图。从图4相对于图3的轮廓变化及表2的极值分布范围可知，地形产生的扰动影响较大，尤其是高山密布区域的青藏地区。所以当完成地形扰动高频信号滤波后，会凸显地球内部构造等中低频信息。图4中，纬度方向在塔里木盆地、青藏高原和喜马拉雅山南部附近区域存在3条明显的纬度方向梯度带，同时在太平洋地区表现出大片负异常；相对前者，图2（b）中经度梯度带的数量明显多于纬度方向，东北－太行－武夷山梯度带清晰可见，并在经度95°左右有一条纵穿中国大陆的中央梯度带［2］；垂向导数的异常结果总体呈现出陆地为正、海洋为负的图形分布。

在图4基础上经Airy－Heiskanen模型改正后的均衡重力梯度异常见图5，其统计结果见表3。均衡异常反映了由地壳运动导致的静力平衡偏离程度。因为均衡失衡需要相应均衡调整而产生新的构造运动，所以通常重力失衡带就是活动构造带，并且 地 震 多 发 生 在 附 近 异 常 梯 度 带 上［3，20，21］。如图所示，均衡异常图和GOCE 卫星观测到的扰动异常具有总体相似性。在喜马拉雅山脉附近地区，所有重力梯度结果都显示该地区属于非均衡状态。异常梯度带按照图5（c）显示，山脉南侧为均衡负异常而北侧为正异常，可能表示印度洋板块的碰撞作用导致北部地壳在增厚［22］。此外，在中国区域内有4个明显的均衡异常区域，从3个分量图像及重力梯度的几何图形意义［15］可知，这些异常基本呈现点状分布。对比文献［21］的重力均衡异常结果发现，在31°N、103°E的汶川地区附近有两个相近的异常区域，且汶川地区异常值较大，但经过汶川地震能量释放后该区均衡异常已相对减弱。在太平洋区域，均衡异常图形显示的是和环太平地震带高度符合的正负异常相对的海沟－海弧分布。

图3 GOCE高度中国及其邻区扰动重力梯度图Fig.3 The map of gravity gradient disturbance in China and its neighboring area at GOCE altitude

图4 经过地形改正后的中国及其邻区扰动重力梯度图Fig.4 The map of gravity gradient disturbance after topography correction in China and its neighboring area

表1 GOCE高度中国及其邻区扰动重力梯度结果统计Tab.1 The statistics of gravity gradient disturbance in China and its neighboring area at GOCE altitude

表2 经过地形改正后中国及其邻区的扰动重力梯度结果统计Tab.2 The statistics of gravity gradient disturbance after topography correction in China and its neighboring area

图5 中国及其邻区均衡重力梯度异常图Fig.5 The isostatic anomaly map of gravity gradient disturbance in China and its neighboring area

表3 中国及其邻区均衡重力梯度异常结果统计Tab.3 The isostatic anomaly statistics of gravity gradient in China and its neighboring area

3 结 语

本文在球坐标下采用球谐谱方法计算地形和均衡影响，并给出相应的重力梯度异常结果。由于地形和均衡公式都基于球面模型，从而有效避免了大空间范围计算时的平面误差影响。从地形改正结果初步分析，较好地符合了一些地质构造的先验结论。从均衡异常图的初步解读，与地壳运动和地震活动带有较好的一致性。文中所示梯度分量能从多角度提供原始信息用于结果分析，但文中没有考虑均衡模型横向密度不均，重力梯度在地球物理学中的应用解释尚未完善，需要在以后研究中加强。

［1］Álvarez O，Gimenez M，Braitenberg C，et al.GOCE Satellite Derived Gravity and Gravity Gradient Corrected for Topographic Effect in the South Central Andes Region［J］.Geophysical Journal International，2012，190（2）：941－959

［2］马宗晋，高祥林，宋正范.中国布格重力异常水平梯度图的判读和构造解释［J］.地球物理学报，2006，49（1）：106－114（Ma Zongjin，Gao Xianglin，Song Zhengfan.Analysis and Tectonic Interpretation to the Horizontal Gradient Map Calculated from Bouguer Gravity Data in the China Mainland［J］.Chinese Journal Geophysics，2006 49（1）：106－14）

［3］方盛明，冯锐，田长征，等.亚洲中部地区均衡重力异常特征及地震活动性［J］.地震学报，1997，19（6）：650－654（Fang Shengming，Feng Rui，Tian Changzheng，et al.Isostatic Gravity Anomaly and Seismic Activity in Central Asia［J］.Acta Seismologica Sinica，1997，19（6）：650－654）

［4］张赤军，方剑，马宗晋.均衡异常与现代构造应力场的初步研究——以东海及其东缘海为例［J］.地震学报，2003，25（1）：32－39（Zhang Chijun，Fang Jian，Ma Zongjin.Preliminary Study of Isostatic Anomaly and Modern Tectonic Stress Field［J］.Acta Seismologica Sinica，2003，25（1）：32－39）

［5］方剑.中国及邻区均衡重力异常及其地球动力学特征［D］.北京：中国地震局地质研究所，2006（Fang Jian.Isostatic Gravity Anomaly and Its Geodynamic Characters in China and Its Adjacent Regions［D］.Institute of Geology，CEA，2006）

［6］罗志才，陈永奇，宁津生.地形对确定高精度局部大地水准面的影响［J］.武汉大学学报：信息科学版，2003，28（3）：340－344（Luo Zhicai，Chen Yongqi，Ning Jinsheng.Terrain Effect in the Determination of Local High Precise Geoid［J］.Geomatics and Information Science of Wuhan University，2003，28（3）：340－344）

［7］黄谟涛，翟国君.利用FFT 技术计算地形改正和间接效应［J］.测绘学院学报，2000，17（4）：242－246（Huang Motao，Zhai Guojun.Terrain Correction and Indirect Effects Using FFT Technology［J］.Journal of Institute of Surveying and Mapping，2000，17（4）：242－246）

［8］Tziavos I N，Sideris M G，Forsberg R，et al.The Effect of the Terrain on Airborne Gravity and Gradiometry［J］.Journal of Geophysical Research：Solid Earth（1978 –2012），1988，93（B8）：9 173－9 186

［9］Zhu L.Gradient Modelling with Gravity and DEM［D］.The Ohio State University，2007

［10］Heck B，Seitz K.A Comparison of the Tesseroid，Prism and Point－mass Approaches for Mass Reductions in Gravity Field Modelling［J］.Journal of Geodesy，2007，81（2）：121－136

［11］Wild F，Heck B.Topographic and Isostatic Reductions for Use in Satellite Gravity Gradiometry［C］.VI Hotine－Marussi Symposium on Theoretical and Computational Geodesy，2008

［12］Grombein T，Seitz K，Heck B.Untersuchungen zur Effizienten Berechnung Topographischer Effekte auf den Gradiententensor am Fallbeispiel der Satellitengradiometriemission GOCE［M］.KIT Scientific Publishing，2010

［13］Tsoulis D.A Comparison between the Airy／Heiskanen and the Pratt／Hayford Isostatic Models for the Computation of Potential Harmonic Coefficients［J］.Journal of Geodesy，2001，74（9）：637－643

［14］Novák P，Grafarend E W.The Effect of Topographical and Atmospheric Masses on Spaceborne Gravimetric and Gradiometric Data［J］.Studia Geophysica et Geodaetica，2006，50（4）：549－582

［15］Saad A H.Understanding Gravity Gradients—A Tutorial［J］.The Leading Edge，2006，25（8）：942－949

［16］Hirt C，Kuhn M，Featherstone W E，et al.Topographic／Isostatic Evaluation of New－Generation GOCE Gravity Field Models［J］.Journal of Geophysical Research：Solid Earth（1978–2012），2012，117（B5）

［17］Mayer－Gürr T，Rieser D，Höck E，et al.The New Combined Satellite Only Model GOCO03s［C］.GGHS2012，Venice，Poster，2012

［18］张兴福，刘成.综合EGM2008 模型和SRTM／DTM2006.0 剩余地形模型的GPS 高程转换方法［J］.测绘学报，2012，41（1）：25－32（Zhang Xingfu，Liu Cheng.The Approach of GPS Height Transformation Basedon EGM2008 and SRTM／DTM2006.0Residual Terrain Model［J］.Acta Geodaeticaet Cartographica Sinica，2012，41（1）：25－32）

［19］Pavlis N K，Holmes S A，Kenyon S C，et al.An Earth Gravitational Model to Degree 2160：EGM2008［J］.EGU General Assembly，2008：13－18

［20］蒋福珍，张赤军，倪志宏，等.青藏高原均衡场与非潮汐重力测量［J］.地球物理学报，1989，32（4）：465－469（Jiang Fuzhen，Zhang Chijun，Ni Zhihong，et al.Isostatic Field and Non－tidal Gravity Measurement in Qinghai－Xizang Plateau［J］.Chinese Journal Geophysics，32（4）：465－469）

［21］王懋基，程振炎.均衡异常与地壳结构［J］.地质学报，1982，56（1）：52－61（Wang Maoji，Cheng Zhenyan.Isostatic Anomaly and Crustal Structure［J］.Acta Geologica Sinica，1982，56（1）：52－61）

［22］刘燕平，蔡少华.青藏地区的均衡异常研究［J］.地壳形变与地震，1988（4）：8－12（Liu Yanping，Cai Shaohua.Research of Gravity Anomalies in Qinghai－Tibet Plateau［J］.Crustal Deformation and Earthquake，1988（4）：8－12）