机器人BP神经网络避障控制模型构建及仿真*
张素芹
(西安工业大学 理学院,西安710021)
随着智能机器人的研究和计算机技术的发展,将信息融合技术应用在智能移动机器人,已经发展到一定水平.智能机器人就是通过各类型传感器获取大量信息来决策的,如何有效快速处理从传感器接收到的信息显得尤为重要,目前常用的方法是信息融合处理技术.经过融合技术处理后的信息将直接决定机器人能否准确、及时地获得并解析它周围的环境信息,机器人通过使用融合处理过后的信息,才能独立的完成决策.
机器人在不同的环境中进行导航和避障时选择的算法不同,避障算法分为传统算法和智能算法,传统算法中有可视图法、栅格法、自由空间法、拓扑法及人工势场法等,文献[1]对这些方法做了详细的阐述,智能算法主要有模糊控制法[2-3]和神经网络法[4-5].目前信息融合领域在大量应用误差后向传播(Back Propagation,BP)神经网络.文献[6]采用Hopfield神经网络通过使用模糊神经元的方法进行路径规划和避障;文献[7]通过使用神经网络进行避障的同时与混合智能系统(Hybrid Intelligent Systems,HIS)相连接,可以使移动机器人的认知决策避障的能力和人相近;文献[8]在得到移动机器人和障碍物之间距离和角度信息后,采用4层神经网络设计控制器,在解决移动机器人避障时间和避障效率上有较好的效果;文献[9]采用生物激励神经网络的方法解决非静态环境下动态避障问题.信息融合神经网络算法具有良好的容错能力、适应能力,还具有一定的记忆能力和并行处理能力.但这些算法会随着输入节点数和隐含层数的增加,结构将变得越来越复杂,网络的收敛速度将会变得很慢,因此近几年国内外神经网络研究者都想找到可以优化神经网络或者是否能将几种方法进行整合,以此来提高它的处理速度.针对存在的这些问题,文中结合机器人在导航避障过程中实际技术要求,通过BP神经网络算法收敛分析对算法进行改进,提出一种新型机器人二级BP神经网络避障控制模型,对该模型进行仿真,以期消除传统机器人BP神经网络避障模型权值调节收敛慢的瓶颈,为机器人实时避障提供新的控制模型.
1 机器人BP神经网络避障控制模型构建
1.1 BP神经网络算法原理
BP神经网络在模式识别方面有较好的非线性逼近能力及多层感知能力[10].在识别时,采用训练BP神经网络与工作BP神经网络两种不同工作种类的网络模型,这两模型具有相同的层数和节点数.BP神经网络拓扑结构分为输入层、隐含层与输出层,每层的节点数目根据实际应用来确定.训练BP神经网络的主要作用是根据采样数据集对网络进行训练,通过调节输入层与隐含层、隐含层与输出层的连接权值矩阵直到网络输出层的误差为零.工作BP神经网络使用训练过的权值矩阵对障碍物进行识别,所以这种模型识别障碍物的时间分成训练时间和工作时间.通过调节学习率可以提高训练的速度,减少训练时间从而提高系统的效率.基于BP神经网络的训练过程包括前向计算及误差的反向传播.
1)前向计算
设定网络输出层神经元m的输入为netm,输出为ym,隐含层任意神经元i的输出为yi,输入层任意神经元n的输出为yn,输出层中每个神经元的输入值是隐含层中每一个神经元的输出与连接权值之后的求和乘积,wmi是输出层神经m与隐含层神经元i间的连接权值,win是隐含层神经元i与输入层神经元n之间的连接权值.
对于输出层有

其中f(netm)为神经元m激活函数.
对隐含层有

神经元的激活函数取Sigmoid,则输出层的激活函数为

式中:hm为神经元m 的阈值;θ0为控制函数Sigmoid的斜率.
2)误差的反向传播
误差反向传播的目的是修正连接权值wmi和win使误差,使其达到最小化.所以连接权值wmi和win应当沿着输出层误差减少方向进行调节.
假设在输入模式xp(p为输入神经元节点数)作用下,若输出层的第k个神经元的期望输出值为dpk,实际输出值为ypk,输出层输出方差Ep为

式中:η为学习率;Δpwmi为修正权值;δpm为学习规则中神经元m的误差值.
1.2 BP神经网络算法改进
传统的BP神经网络存在权值收敛慢的问题,从式(8)看出,权值调节收敛的速度与学习率调节因子大小有一定的关系,每个神经元的连接权值是通过学习调节沿着梯度下降方向进行的.一旦学习规则固定,学习率的调节会影响学习过程的收敛速度.传统的BP神经网络法学习率是固定不变的,无法适应在学习过程中发生较为复杂的的状态变化.过大的学习率会使系统趋向不稳定,但过小的学习率将导致训练时间较长,收敛速度变慢,不过能保证网络的误差值不跳出误差表面的低谷而最终趋于最小的误差值,所以一般学习率在0.1~0.9之间选取.通过引入调节因子,调节学习率,改善权值收敛的速度,改善学习效果、加快学习过程.学习率的调节因子为学习率η的函数,那么权值修正公式为
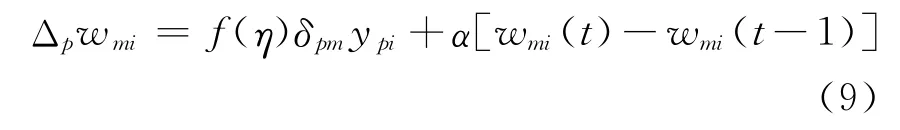
式中:f(η)为学习率的调节因子;α为惯性系数,0<α<1;wmi(t)为t次训练时修正权值.
为减小学习过程中因为权值变化而引起的震荡,给式(9)中引入一惯性项α[wmi(t)-wmi(t-1)],相当于给权值调节加入阻尼项,可避免BP神经网络陷入一种局部极小值点状态.根据可变学习速 率 反 向 传 播 (Variable Learning Rate Back Propagation,VLBP)算法[11],学习率的大小可以根据均方误差做出适当的调整.当E(k+1)小于E(k)时,增加学习率;当E(k+1)大于E(k)时,就减少学习率.引入调节学习率的增量因子kinc和减量因子kdec,那么学习率的调节因子f(η)的选取规则为

若E(k+1)比E(k)小时说明权值修正方向正确,这种情况应该要增大学习率;若E(k+1)比E(k)大时,说明修正过大,适当减少学习率,否则权值系数会出现反复震荡导致不能收敛.kinc和kdec的值依据以往经验进行初步设置,通过不断调节其大小,直到最后得到理想的训练步长.
1.3 二级BP神经网络信息融合系统模型建立
二级BP神经网络的信息融合系统模型如图1所示,系统模型分为两个子神经网络,子神经网络用Sub1和Sub2表示.距离信息是通过超声波传感器和红外传感器两种传感器检测.通过电荷耦合器件(Charge Coupled Device,CCD)摄像机检测的图像信息和通过Sub1输出的距离信息输入神经网络Sub2.其中Sub1由三层BP神经网络组成,其输入层有9个神经元,分别表示3个红外传感器和6个超声波传感器测得的距离;输出层有3个神经元,分别表示距离正前方、左前方和右前方障碍物的距离;隐含层中神经元的个数c为

式中:m为输入层中神经元的个数;n为输出层中神经元的个数.
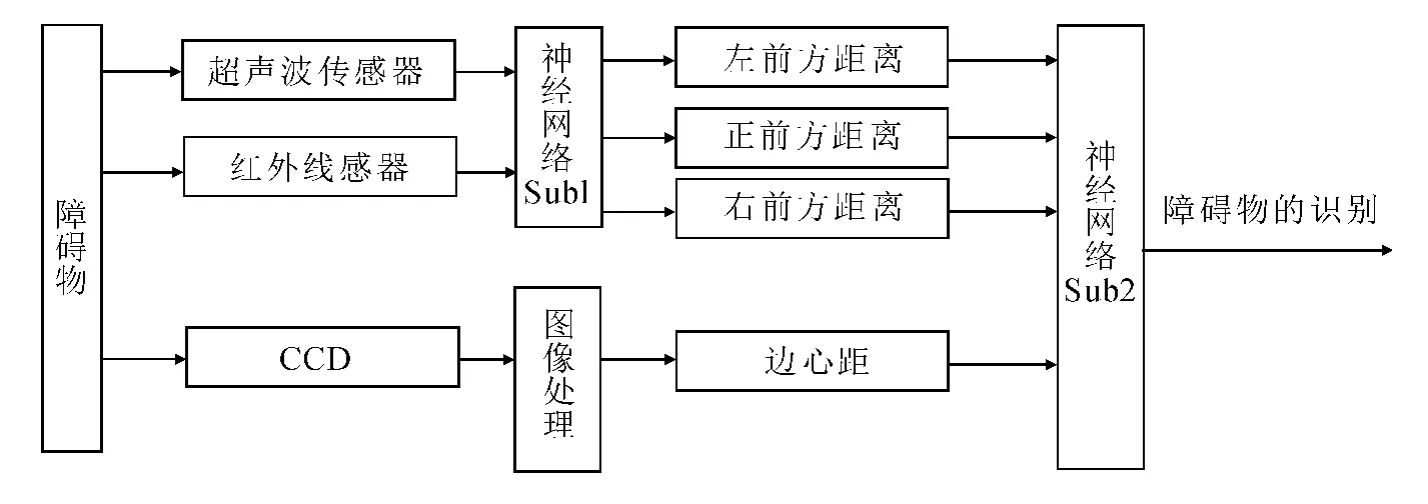
图1 二级BP神经网络系统结构Fig.1 The structure of two level BP neural network system
对于障碍物的大小信息以及形状等信息,机器人是无法预先感知的,因此可根据检测到的距离信息以及通过摄像机获取障碍物的图像信息得出关于障碍物的三维图像信息,从而实现对障碍物类型快速识别.若使用传统单级BP神经网络,输入层有17个节点,输出层有5个节点,则隐含层的节点数为15时,才能实现对障碍物的有效识别,但此时系统结构会变得复杂,计算量变大,系统的实时性受到一定的限制.
2 仿真分析
进行仿真实验时,首先进行障碍物的类型设置,可大体初步分为五种形式:长方体、圆柱体、椭球体、球体及等腰梯形.在进行机器人二级BP神经网络避障控制模型学习训练时,学习参数设置如下:最大训练步数为100,训练误差最小值为0.001.惯性系数α的值在很多实际实验中选取0.9~1之间,本次仿真实验选取值为0.95.学习率η的取值通常在0~1之间,本次仿真实验选取η=0.8.实验采用调节学习率增减量因子动态的改变学习率的大小,从而减少训练步长.假设机器人以0.2m·s-1速度向前方行驶,设置一组障碍物形体值并对每个障碍物每隔10°进行取样作为训练集,然后对障碍物的大小稍作改变,每隔15°采样作为测试集;在仿真实验中通过设置参数kinc和kdec实现学习率大小的动态调节,一般在开始训练时,学习率值应当取大一些,在此取kinc为1.5,kdec为0.3.神经网络训练误差-步长曲线图如图2所示.由图2看出,需60个步长才使得训练误差小于0.001.
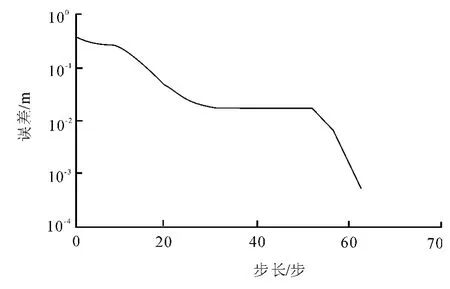
图2 kinc=1.5,kdec=0.3时神经网络训练误差-步长曲线图Fig.2 The training step of kinc=1.5,kdec=0.3
通过反复调整学习率参数,确定出kinc和kdec最佳取值,即当kinc=1.2,kdec=0.5时,神经网络训练过程达到最优,其神经网络训练误差-步长曲线图如图3所示.从图3看出,只需30步就能使训练误差小于0.001.步长达到全局最小,步长减小能显著缩短网络训练时间,提高学习效率.
机器人二级BP神经网络避障控制模型训练结束后即可对障碍物进行识别,避障控制模型对障碍物的识别结果见表1.从表1可看出,该模型能有效识别障碍物.随着识别次数增加时,该模型的识别率会不断增加.
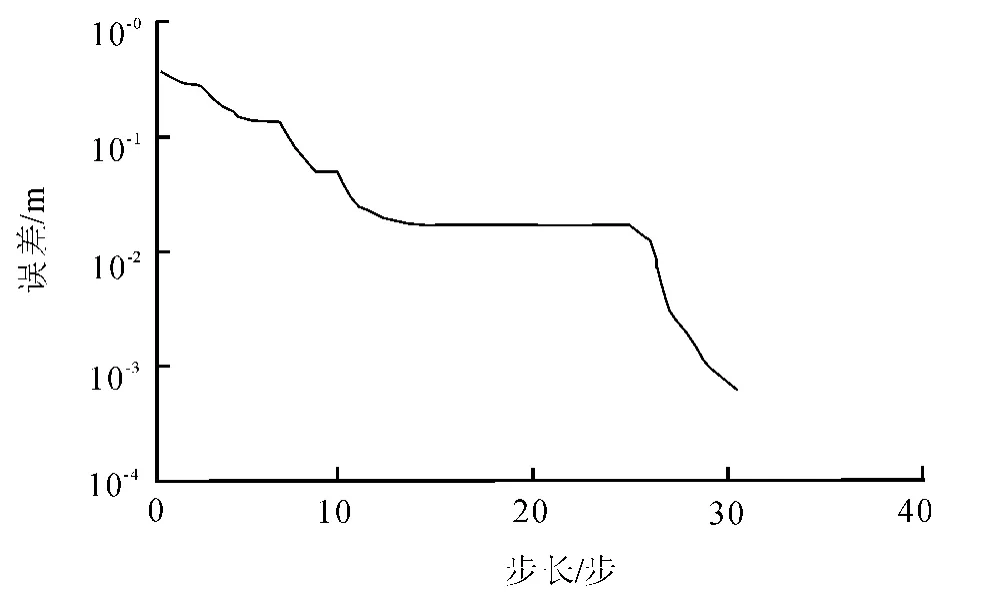
图3 kinc=1.2,kdec=0.5时神经网络训练误差-步长曲线图Fig.3 The training step of kinc=1.2,kdec=0.5

表1 机器人二级BP神经网络避障控制模型的障碍物识别率Tab.1 Obstacle recognition rate of robot
按照障碍物大小,采用相应比例构建机器人工作空间,已知机器人工作空间中的起始点和目标点.机器人导航避障轨迹如图4所示,图4中轨迹坐标记为(X,Y).
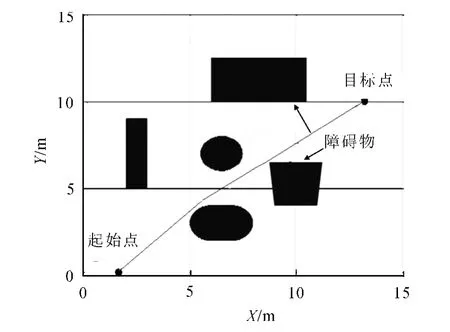
图4 机器人导航避障轨迹Fig.4 Trajectory of robot navigation
从图4中看出机器人导航轨迹避开了障碍物,且沿着一条最短路径到达目标点,导航效果优于传统BP神经网络避障控制模型,运动路径趋近最优直线路径.通过引入学习率调节因子有效缩短了机器人目标点到达时间,机器人导航效率得以提升.
3 结 论
1)通过引入学习率调节因子kinc和kdec,提出了学习率动态调节方法.基于该方法给出了二级BP神经网络算法.该算法在权值调节收敛速度方面优于传统单级BP神经网络算法,通过减少训练步长能显著节约网络训练时间,提高学习效率.
2)通过BP神经网络算法的改进,给出了新型机器人二级BP神经网络避障控制模型.仿真结果表明,该模型实现了障碍物的快速识别,其障碍物识别率达到80.5%~99.5%,导航效率优于传统BP神经网络模型,运动路径趋近最优直线路径,有效缩短了机器人到达目标点时间.
[1] 常健,吴成东.移动机器人避障方法综述[J].仪器仪表学报,2010,31(8):439.CHANG Jian,WU Cheng-dong.Survey of Obstacle A-voidance of Mobile Robot[J].Chinese Journal of Scientific Instrument,2010,31(8):439.(in Chinese)
[2] 陈华志,谢存禧.移动机器人避障模糊控制[J].机床与液压,2004(11):77.CHEN Hua-zhi,XIE Cun-xi.Fuzzy Technique for Mobile Robot Obstacle Avoidance[J].Machine Tool & Hydraulics,2004(11):77.(in Chinese)
[3] 任亚楠,贾瑞清.基于超声波传感器的移动机器人避障系统研究[J].中国测试,2012,38(3):76.REN Ya-nan,JIA Rui-qing.Research on Obstacle A-voidance System of Mobile Robot Based on Ultrasonic Sensor[J].China Measurement & Test,2012,38(3):76.(in Chinese)
[4] 王丙强,宋弘.二级BP网络在机器人传感器融合中的应用[J].微计算机信息,2009,25(23):192.WANG Bin-qiang,SONG Hong.The Application of Two-level Neural Networks in Sensors Fusion of the Robot [J].Microcomputer Information,2009,25(23):192.(in Chinese)
[5] 郭琦,洪炳熔.基于人工神经网络实现智能机器人的避障轨迹控制[J].机器人,2002,24(6):508.GUO Qi,HONG Bing-rong.Trajectory Control with Obstacle Avoidance of Mobile Robots Based on Neural Network[J].Robot,2002,24(6):508.(in Chinese)
[6] GLASIUS R,KOMODA A,GIELEN S C.Neural Network Dynamics for Planning and Obstacle Avoidance[J].Neural Networks,1995,8(1):125.
[7] CHOHRA A,FARAH A,BELLOUCIF M.Neuro-Fuzzy Expert System E_S_CO_V for the Obstacle A-voidance Behavior of Intelligent Autonomous Vehicles[J].Advance Robotics,1999,12(6):629.
[8] PARHI D R,SINGH M K.Real-Time Navigational Control of Mobile Robots Using an Artificial Neural Network[J].Proceedings of the Institution of Mechanical Engineers,Part C:Journal of the Mechanical Engineering Science,2009,223(7):1713.
[9] SIMON X,YANG M M.Neural Network Approaches to Dynamic Collision-free Trajectory Generation[J].IEEE Transaction on Systems,Man,and Cybernetics Part B:Cybernetics,2001,31(3):302.
[10] 储琳琳,郭纯生.浅析BP神经网络算法的改进和优化[J].科技经济市场,2009(4):4.CHU Lin-lin,GUO Chun-sheng.Analysed the BP Neural Network Algorithm of Improvement and Optimized[J].Science and Technology Economic Market,2009(4):4.(in Chinese)
[11] 张华节,李璀.学习速率连续变化的BP神经网络算法[J].四川兵工学报,2011(4):61.ZHANG Hua-jie,LI Cui.The BP Neural Network Algorithm with Continuous Learning Rate[J].Journal of Sichuan Ordnance Industry,2011(4):61.(in Chinese)

