平台巴西劈裂试验确定岩石抗拉强度的理论分析

黄耀光，王连国， ，陈家瑞，张继华

（1.中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州，221116；2.中国矿业大学 力学与建筑工程学院，江苏 徐州，221116）

1 引 言

由于岩石属于典型脆性材料，故采用直接拉伸试验来确定其抗拉强度极为困难。因而，巴西圆盘劈裂试验被作为测定岩石抗拉强度的间接方法[1]，其经典力学简化模型如图1(a)所示。但该方法需对试样施加对径压缩载荷，这使得加载线附近由于强烈应力集中而发生压破坏，违背了巴西劈裂试验中心起裂[2－3]的假设，从而使所测抗拉强度与真实值存在较大差异。为了降低标准巴西劈裂试验中对径线加载所引起的应力集中程度，一般有两种方法：一种是弧形加载巴西圆盘试验法[2，4－11]。文献[6]用复变函数法得到巴西圆盘内的全应力和位移场理论解，并用试验验证了解的有效性。而文献[5，7－8]通过试验与数值模拟相结合的方法，得到不同弧形加载角下巴西圆盘内的应力状态和试样破坏过程。文献[9－11]求得了巴西圆盘受抛物线型载荷下的应力和位移场，并考虑了不同加载角度和载荷类型对圆盘内应力和位移分布的影响。尽管弧形加载巴西劈裂试验能降低应力集中程度，但由于加载困难以及加载弧上应力的不均匀性，使其不易保证巴西试样发生中心起裂。

另一种是图1(b)所示的平台巴西劈裂试验。王启智等[3，12]将文献[13]提出的确定岩石断裂韧度的平台巴西劈裂试验推广用于确定岩石抗拉强度，借助标准巴西圆盘的应力解，利用有限元数值法研究了平台圆盘内的应力分布规律及位移解，得到保证岩石试样中心起裂所需的临界平台加载角，进而得出岩石的抗拉强度经验公式。而后王启智等[14]采用平台巴西劈裂试验测得大理岩的抗拉强度，证明该试验的合理性。在此基础上，尤明庆等[15－16]利用有限元数值法得到不同平台加载角下圆盘内的应力分布特征：圆盘内应力随平台加载角增大而减小；并结合4类典型岩石的平台巴西劈裂试验指出，平台加载角应保持在20°～30°之间为最佳。于庆磊[17]、孟京京[18]等分别用有限元和离散元数值法研究了平台加载角对非均质巴西试样的应力状态和劈裂破坏模式的影响。而喻勇等[19]利用三维弹性有限元法，较全面地分析了圆盘高径比和泊松比等因素对平台圆盘应力分布的影响，并基于Mohr强度理论给出了平台巴西劈裂试验测定岩石抗拉强度的数值计算公式。

图1 标准和平台巴西劈裂试验力学模型Fig.1 Mechanical models of standard and flattened Brazilian splitting tests

由于以上研究平台巴西劈裂试验时，主要采用的是有限元或离散元数值分析方法，并以标准巴西圆盘内的应力理论解来代替平台巴西圆盘内的应力状态，这使所得结果出现偏差，而且缺少相应的理论分析作为支撑。因此，基于二维弹性理论，借助半无限平面体受竖直线荷载的符拉芒解，采用应力叠加方法求得平台巴西圆盘内的应力解析解，并用有限元数值法对该应力解加以验证。以此为基础，从理论上分析了平台加载角对圆盘应力分布规律的影响，获得保证平台巴西圆盘试样中心起裂的最优加载角度以及计算岩石抗拉强度的理论公式。

2 平台巴西圆盘的应力理论解

假定平台巴西圆盘是均匀各向同性弹性体，并将实际试验中的近似均布位移加载简化为均匀对弦载荷加载，从而建立如图1(b)所示的直角坐标系下的平台巴西劈裂试验力学分析模型。在应力求解过程中，认为平台巴西圆盘所受对弦均布载荷是作用在半无限平面体边界上的，其内任意点的应力是由上、下加载平台所受均布载荷产生的径向应力叠加而成。由此，依据圣维南原理，可求得半无限平面体下平台巴西圆盘边界上和圆盘内任意点的应力解。但由于实际平台巴西劈裂试验并非是半无限平面体，其在圆盘边界上应保持自由边界。所以，应将所得圆盘边界上的应力解以反力的形式叠加到圆盘内的应力解之上，从而求得平台巴西圆盘的应力理论解。

2.1 平台巴西圆盘边界上的应力解析解

在平台巴西劈裂试验中，设圆盘半径为R，圆盘厚度为t，平台加载角为2α，如图2所示，则加载平台宽度可表示为

式中：α为弧度。

假设试验机所施加的集中力P 均匀作用在厚度为t 的加载平台上，则力P 与平台上的均布载荷q 之间满足如下关系：

从而得到由集中力P 所表示的平台上的均布载荷q为

为了求得平台巴西圆盘边界上任意点M 的应力，可在上下加载平台处任取一对称微元ds，其微元力为dF=qd s。假定该微元力分别作用在两个不同的半无限平面体上，则每个微元力都将在半无限平面体内产生径向分布应力。因此，根据圣维南原理，可由弹性力学中半无限平面体受竖直线荷载的符拉芒解[20]得到M 点处的两个径向应力分别为（以拉应力为正，压应力为负）

式中：r1和r2分别为微元力作用点与边界点M 的距离；θ1和θ2则分别为r1、r2与铅垂方向的夹角。

设直线τ为点M 所在圆周的切线，过M 作MN 与τ 垂直，则MN为圆盘直径。同时由于平台加载角相对较小，所以有：∠MAN≈∠MA′ N=，∠MBN≈∠MB ′N=。又由于在△MAN中，有∠MNA=θ2，则得∠AMN=；在△MBN中，∠MNB=θ1，则得∠BMN=具体见图2。于是，根据Cauwelaert等[21]中的坐标变换公式，采用应力叠加方法可得点M 处的正应力dσn和切应力dστ分别为

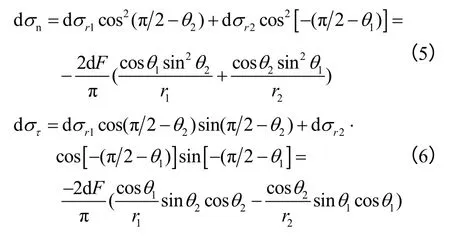
图2 平台巴西圆盘边界任意点的应力计算示意图Fig.2 Schematic diagram of stress calculation at arbitrary boundary points on flattened Brazilian disk

因在△MAN和△MBN中，存在如下几何关系：

则将式（7）分别代入式（5）、（6）中，可得

而在△AMB中有：∠AMB=π -(θ1+θ2)，则由三角函数关系：可得

则将式（9）代入式（8）可得

因此，平台巴西圆盘边界上任意点M 处的应力可沿受均布载荷q 的加载平台进行积分求得

2.2 平台巴西圆盘的应力解析解

由2.1节可知，平台巴西圆盘内任意点 M (x ，y)处的径向分布应力仍可表示成式（4）的形式。利用弹性力学[20]和Cauwelaert[21]中的坐标变换公式，可得直角坐标系下圆盘内的微元应力分量为

再将式（12）中相同方向的微元应力分量进行叠加，得到平台圆盘内的3个应力分量为

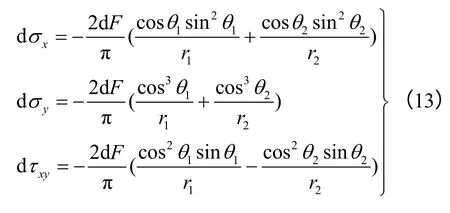
又因在圆盘内满足如下关系式：

故将式（14）代入式（13），并沿着所受均布载荷的加载平台进行积分，再叠加由2.1节所得的均布拉应力，最后，在圣维南原理下可求得平台巴西圆盘内的应力分量为

图3 平台巴西圆盘内任意点的应力计算示意图Fig.3 Schematic diagram of stress calculation at arbitrary points inside flattened Brazilian disk

3 平台加载角对巴西圆盘应力分布的影响

3.1 标准巴西圆盘的应力理论解

在标准巴西劈裂试验中，对径压缩载荷下圆盘内任意点的应力经典解可表示为[19，22]

而Wang等[3，12]以式（19）的应力分量来代替平台巴西圆盘内的应力状态，并结合有限元数值分析法给出了平台巴西劈裂试验测定岩石抗拉强度的经验公式为

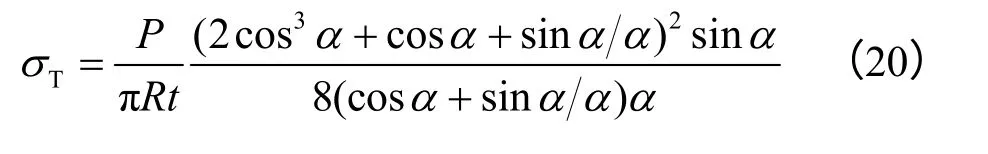
3.2 平台巴西圆盘应力解的数值验证

因为在实际的平台巴西劈裂试验中，平台巴西圆盘受到近似均布位移加载作用，这与本文中的均布应力加载作用存在差异。但根据圣维南原理，其影响主要集中在加载平台附近，而对圆盘中心附近应力结果影响较小。并且由于研究平台巴西劈裂试验的有限元数值分析法已较为成熟[3，12－13，15－17，19]，因此，采用该方法将不同平台加载角下的圆盘应力数值解与应力理论解进行对比分析，以验证求解平台巴西圆盘应力解析解方法的正确性。

在有限元数值分析中，选择建立包含加载压头的平台劈裂二维模型，通过加载压头和平台巴西试样之间的接触单元[23]来保证实际试验中的均布位移加载，其接触摩擦系数设为0.05，以近似试验中的理想光滑接触。该模型的半径R=25 mm，平台加载角分别为10°、20°、30°、40°，其平台处网格单元数目为10，而其他网格单元边长为1 mm。平台圆盘试样的弹性模量E 取为80 GPa，其泊松比为0.2。又为了保证加载压头的刚度，取其弹模为试样的100倍，而泊松比为0.3。模型下加载压头的左端节点固定x、y 向位移，右端节点固定y 向位移，并同时在上下加载压头处施加均布压缩载荷q，q 值由式（3）计算所得，其中试验载荷P=15 kN。数值计算模型如图4所示。

经数值计算后，选取平台巴西圆盘加载直径上的水平应力σx和垂直应力σy作为比较验证对象，其应力无量纲化（σ/(P/πRt)）后随平台加载角的变化规律分别由图5、6给出。而表1则给出了不同加载角下圆盘内的最大压拉应力比。需注明的是，由于加载点处应力趋于无穷大，所以表1中的的最大应力取自于近加载点处的值，而非加载点。

图4 平台巴西劈裂有限元数值计算模型Fig.4 Finite element numerical calculation model of flattened Brazilian splitting test

图5 加载直径上的无量纲水平应力Fig.5 Non-dimensional horizontal stresses along loaded diameter

图6 加载直径上的无量纲垂直应力Fig.6 Non-dimensional vertical stresses along loaded diameter

表1 两种圆盘内的无量纲压拉应力比Table 1 Ratios of non-dimensional compressive stress to tensile stress inside two kinds of disk

综合分析图5、6可知，在4个不同的平台加载角下，圆盘内加载直径上的水平应力σx和垂直应力σy的理论解和有限元数值解的变化曲线仅在加载平台附近出现较大分离，而在远离加载平台处基本重合。这主要是因为理论求解和数值求解时，平台加载处的加载方式不同而引起的，其结果符合圣维南原理。因此，经对比分析表明前文的理论求解方法是正确合理的。

从图5中可以看出，水平拉伸应力σx的最大值皆出现在圆盘中心附近，并从中心向两加载平台逐渐变小，甚至变为水平压缩应力。而且随着平台加载角增大，平台巴西圆盘内的水平拉伸应力值缓慢减小，其从平台加载角为5°时的0.99降低到50°时的0.65，而水平压缩应力却从33.96急降到2.82，具体如表1所示。同时发现，平台巴西圆盘内的拉伸应力区随着平台加载角的增大而逐渐向圆盘中心缩小，即增大加载角会缩小圆盘内加载方向的拉应力区。

而由图6可知：平台圆盘内的垂直应力σy都从两端的加载平台处向圆盘中心减小。而且在平台巴西圆盘内，随着平台加载角增大，加载平台处的垂直压应力显著减小，其值从平台加载角为5°时的36.01降低到50°时的3.87。从表1中可知，标准巴西圆盘内的最大压拉应力比为50.20，若按通常岩石抗压强度为抗拉强度的10倍计算，则标准巴西试样将会在加载点附近由于压应力过大而发生压破坏。但平台巴西圆盘内的压拉应力比会随着平台加载角增大而减小，当加载角为20°时，其最大压拉应力比已经降低到9.65，此时可认为平台巴西圆盘试样不会发生加载处的压破坏而是发生中心拉破坏。由此发现，增大平台加载角可以明显降低加载处的压应力值和应力集中程度，从而降低巴西试样在加载平台附近发生压缩破坏的可能，为试样率先发生中心拉伸劈裂破坏创造条件。

3.3 标准和平台巴西圆盘应力分布对比分析

由于以上研究的仅是圆盘加载直径上的应力分布特征，缺乏一般性。为了对圆盘内的应力分布有更完整、直观的认识，在此取加载角为30°的平台巴西圆盘内的应力解与标准巴西圆盘进行对比分析。图7、8分别表示无量纲化后圆盘内的水平应力和垂直应力等值线图。

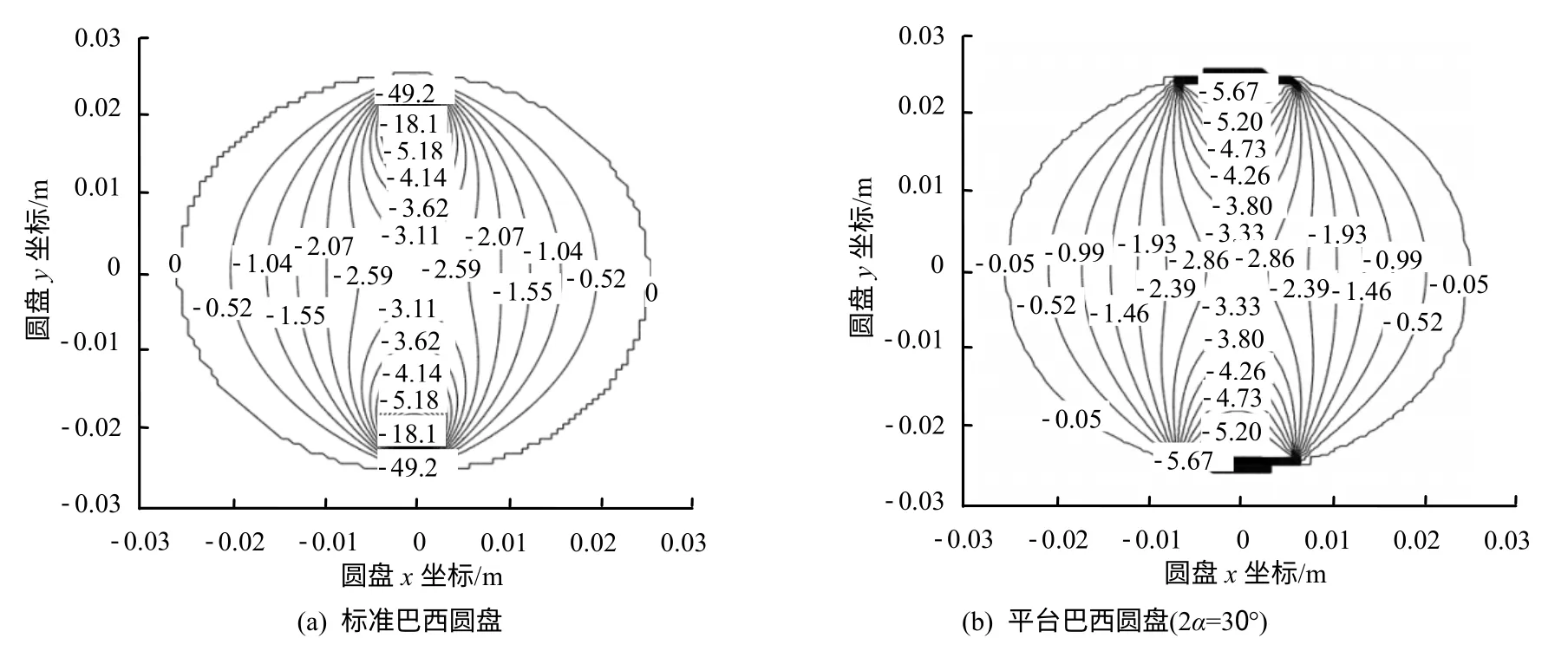
图8 圆盘内的无量纲垂直应力(σy/(P/πRt))Fig.8 Non-dimensional vertical stress inside the disks (σy/(P/πRt))

从图7、8可知，标准巴西圆盘内的水平应力经过加载点而形成中部宽、两端狭长的拉应力区。而平台巴西圆盘内的水平应力是在加载点下方形成环状拉应力区，即加载方向上的拉应力区缩小了，这不利于实现巴西劈裂试验从中心起裂并向两端扩展而发生拉破坏的条件。但相比于标准巴西圆盘，平台巴西圆盘内的水平压应力和垂直应力值在加载点处都有极大地降低，而且在加载点附近的应力分布更加均匀，如图7(b)、8(b)所示。这显著地降低了巴西圆盘加载点附近的应力集中程度，有利于减小试样由于加载点处的压应力强烈集中而发生压破坏的可能性，从而满足巴西试验的中心起裂条件。由此发现，平台巴西圆盘的加载角是控制巴西试验能否成功的关键因素，过大或过小的加载角都不利于巴西试验的进行。因此，有必要确定出最优的平台加载角来同时满足降低压应力集中和保持圆盘内具有较大拉应力区的要求。

4 平台巴西劈裂试验的最优加载角及抗拉强度

4.1 平台巴西劈裂试验的最优加载角

岩石属于典型脆性材料，因此，岩石的破坏通常满足Griffith强度准则[24]。当以拉应力为正，且3个主应力满足 σ1≥σ2≥ σ3关系时，Griffith强度准则可写成如下形式：

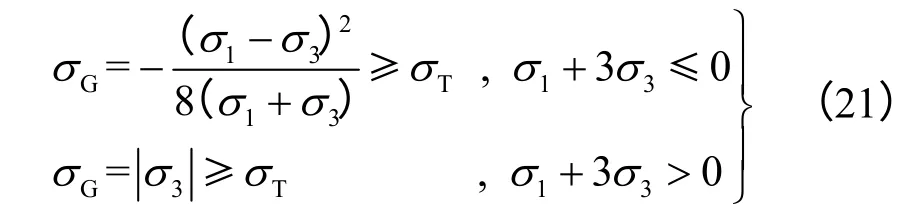
式中：σG为Griffith等效应力；σT为岩石的抗拉强度。

由第2节分析可知，平台巴西圆盘内的加载直径附近是拉应力最大的区域，其成为巴西试样的潜在破坏区。在圆盘加载直径上有x=0，由式（17）计算可得其上剪应力τxy=0，因此，可知加载直径上的水平应力σx和垂直应力σy分别为最大最小主应力，其可由式（15）、（16）计算得到为

所以，式（21）中给出的Griffith强度准则的判定条件可表示为

为了得出Griffith判定条件的大小，将不同加载角下的无量纲化Griffith判定条件值绘于图9中，其中的2α=0°即为标准巴西圆盘。从图9中可知，当加载角小于50°时，有 σ1+3σ3＜ 0恒成立，所以由式（21）可得平台巴西圆盘试样的强度破坏条件为

再将式（22）、（23）代入式（26）即得平台巴西圆盘加载直径上的Griffith等效应力为

将Griffith等效应力进行无量纲化后，其值随平台加载角2α 的变化关系如图10所示。

图9 加载直径上的无量纲Griffith判定条件Fig.9 Non-dimensional Griffith decision conditions along loaded diameter

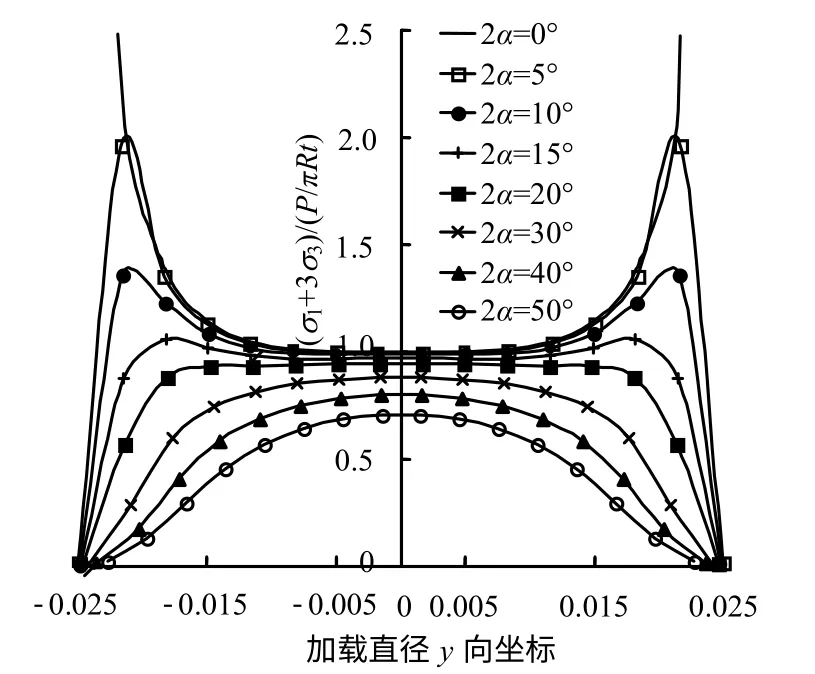
图10 加载直径上的无量纲Griffith等效应力Fig.10 Non-dimensional Griffith equivalent stresses along loaded diameter

从图10可知，当2α＜20°时，平台巴西圆盘加载直径上的Griffith等效应力σG从圆盘中心开始向两端呈现先增大后减小的变化规律，即σG并非在圆盘中心最大，这表明此类平台巴西圆盘并不是从圆盘中心起裂，违背了巴西劈裂试验测定岩石抗拉强度的基本假定，故其不适于用来测定岩石的抗拉强度；当加载角大于等于20°时，平台巴西圆盘加载直径上的Griffith等效应力σG从圆盘中心开始向两端呈逐渐减小趋势，即σG在圆盘中心最大。因此，依据Griffith强度破坏准则可知此类平台巴西圆盘将从圆盘中心开始破坏，其满足巴西劈裂试验测定岩石抗拉强度的中心起裂条件，故可选用2α≥20°的平台巴西圆盘来测定岩石的抗拉强度。

同时由前文分析可知，当2α＞30°以后，增大加载角并不能显著降低平台圆盘内的压拉应力比，如表1所示。因此，综合分析认为，当2α=20°～30°时，平台巴西劈裂试验既能明显降低圆盘内的压拉应力比，又能满足中心起裂条件，故确定平台巴西圆盘的最优加载角为20°～30°。这与Wang[12]和尤明庆[15－16]通过数值和试验方法所得结果相一致。

4.2 平台巴西劈裂试验确定的岩石抗拉强度

当平台巴西劈裂试验处于最优加载角度时，依据Griffith强度准则知试样将从圆盘中心率先开始破坏。因在圆盘中心有x=0，y=0，故由式（24）可知，A1=A3=R2，B1=B3=R2sin αcosα，C1=C3=-α，则由式（26）可得用平台巴西劈裂试验测定岩石抗拉强度的计算公式为

而在弧形加载巴西劈裂试验测定岩石抗拉强度的研究中，Satoh[2]首先得到的岩石抗拉强度公式为

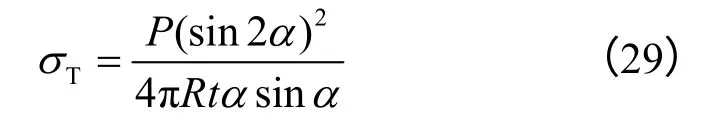
至此，文中给出了3种计算岩石抗拉强度的理论公式，其主要差异是建立力学分析模型时对巴西圆盘受力的简化形式不同。Wang[12]将圆盘受力简化为作用在有限圆弧上的均匀垂直载荷。Satoh[2]则认为圆盘受力是作用在有限圆弧上的均匀径向载荷。而本文分析中是将圆盘受力简化成作用在加载平台上的均布载荷。图11为无量纲化后的各抗拉强度随加载角的变化规律。从图中可知，相比于Wang[12]和Satoh[2]所得的岩石抗拉强度，本文式（27）所得岩石抗拉强度偏小，且随加载角的增大而下降较快，即过大的加载角将使平台巴西劈裂试验失败。但在最优加载角20°～30°之间时，3个抗拉强度的最大相对误差小于4.5%，这即表明所求抗拉强度公式与已有抗拉强度经验公式相符较好。而且表2表明，本文所得抗拉强度理论值与试验值的最大相对误差约为22%，最小相对误差约为4%。考虑到抗拉强度试验的离散型，可认为抗拉强度理论公式是正确的。由此综合证明，前文理论推导岩石抗拉强度的方法是合理的。

图11 无量纲抗拉强度随加载角的变化Fig.11 Variation of non-dimensional tensile strength with loading angle

表2 3类岩石的平台劈裂理论与试验抗拉强度比较Table 2 Comparison of theoretical and experimental tensile strengths for three kinds of rocks

5 结 论

（1）基于二维弹性理论，采用应力叠加法求得平台巴西圆盘内的应力解析解，其与有限元数值解相一致，证明该应力解析解是正确的。

（2）通过研究不同加载角对平台巴西圆盘内应力分布的影响表明：增大平台加载角，可以显著降低平台加载处的压应力和应力集中程度，减小试样发生压裂破坏的可能；但平台巴西圆盘内的拉应力和拉伸区也将缓慢减小，其不利于保证巴西劈裂试验的中心起裂条件。

（3）理论研究得出，过大或过小的加载角都不利于平台巴西劈裂试验的成功，而其最优的平台加载角在20°～30°之间。此时，平台巴西圆盘内的最大压拉应力比相对于标准巴西圆盘有明显减小，其值已小于岩石试样惯用的抗压拉强度比10，故该加载角下的平台巴西劈裂试验最宜被用于确定岩石的抗拉强度。

（4）基于Griffith强度破坏准则，推导得到采用平台巴西劈裂试验测定岩石抗拉强度的理论计算公式，通过比较发现，其与已有的抗拉强度经验公式及试验值相符较好。

[1]ISRM.Suggested methods for determining tensile strength of rock materials[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts，1978，15(3):99－103.

[2]SATOCH Y.Position and load of failure in Brazilian test a numerical analysis by Griffith criterion[J].Journal of the Society of Materials Science，Japan，1987，36(410):1219－1224.

[3]王启智，贾学明.用平台巴西圆盘试样确定脆性岩石的弹性模量，拉伸强度和断裂韧度——第一部分:解析和数值结果[J].岩石力学与工程学报，2002，21(9):1285－1289.WANG Qi-zhi，JIA Xue-ming.Determination of elastic modulus tensile strength and fracture toughness of brittle rocks by using flattened Brazilian disk specimen—Part I：Analytical and numerical results[J].Chinese Journal of Rock Mechanics and Engineering，2002，21(9):1285－1289.

[4]MA C-C，HUNG K-M.Exact full-field analysis of strain and displacement for circular disks subjected to partially distributed compressions[J].International Journal of Mechanical Sciences，2008，50(2):275－292.

[5]YU Y，ZHANG J，ZHANG J.A modified Brazilian disk tension test[J].International Journal of Rock Mechanics and Mining Sciences，2009，46(2):421－425.

[6]MARKIDES C F，PAZIS D，KOURKOULIS S.Closed full-field solutions for stresses and displacements in the Brazilian disk under distributed radial load[J].International Journal of Rock Mechanics and Mining Sciences，2010，47(2):227－237.

[7]ERARSLAN N，LIANG Z Z，WILLIAMS D J.Experimental and numerical studies on determination of indirect tensile strength of rocks[J].Rock Mechanics and Rock Engineering，2012，45(5):739－751.

[8]ERARSLAN N，WILLIAMS D J.Experimental，numerical and analytical studies on tensile strength of rocks[J].International Journal of Rock Mechanics and Mining Sciences，2012，49:21－30.

[9]KOURKOULIS S，MARKIDES C F，CHATZISTERGOS P.The Brazilian disc under parabolically varying load:theoretical and experimental study of the displacement field[J].International Journal of Solids and Structures，2012，49(7):959－972.

[10]MARKIDES C F，KOURKOULIS S.The stress field in a standardized Brazilian disc:The influence of the loading type acting on the actual contact length[J].Rock Mechanics and Rock Engineering，2012，45(2):145－158.

[11]KOURKOULIS S，MARKIDES C F，CHATZISTERGOS P.The standardized Brazilian disc test as a contact problem[J].International Journal of Rock Mechanics and Mining Sciences，2013，57:132－141.

[12]WANG Q Z，JIA X M，KOU S Q，et al.The flattened Brazilian disc specimen used for testing elastic modulus，tensile strength and fracture toughness of brittle rocks:analytical and numerical results[J].International Journal of Rock Mechanics and Mining Sciences，2004，41(2):245－253.

[13]WANG Q Z，XING L.Determination of fracture toughness KIC by using the flattened Brazilian disk specimen for rocks[J].Engineering fracture mechanics，1999，64(2):193－201.

[14]王启智，吴礼舟.用平台巴西圆盘试样确定脆性岩石的弹性模量，拉伸强度和断裂韧度——第二部分:试验结果[J].岩石力学与工程学报，2004，23(2):199－204.WANG Qi-zhi，WU Li-zhou.Determination of elastic modulus tensile strength and fracture toughness of brittle rocks by using flattened Brazilian disk specimen—Part II：Analytical and numerical results[J].Chinese Journal of Rock Mechanics and Engineering，2004，23(2):199－204.

[15]尤明庆，苏承东.平台巴西圆盘劈裂和岩石抗拉强度的试验研究[J].岩石力学与工程学报，2004，23(18):3106－3122.YOU Ming-qing，SU Cheng-dong.Experimental study on split test with flattened disk and tensile strength of rock[J].Chinese Journal of Rock Mechanics and Engineering，2004，23(18):3106－3112.

[16]尤明庆，苏承东.平台圆盘劈裂的理论和试验[J].岩石力学与工程学报，2004，23(1):170－174.YOU Ming-qing，SU Cheng-dong.Split test of flattened rock disk and related theory[J].Chinese Journal of Rock Mechanics and Engineering，2004，23(1):170－174.

[17]于庆磊，唐春安，杨天鸿，等.平台中心角对岩石抗拉强度测定影响的数值分析[J].岩土力学，2008，29(12):3251－3255.YU Qing-lei，TANG Chun-an，YANG Tian-hong，et al.Numerical analysis of influence of central angle of flats on tensile strength of granite in split test with flattened disk[J].Rock and Soil Mechanics，2008，29(12):3251－3255.

[18]孟京京，曹平，张科，等.基于颗粒流的平台圆盘巴西劈裂和岩石抗拉强度[J].中南大学学报 (自然科学版)，2013，44(6):2499－2454.MENG Jing-jing，CAO Ping，ZHANG Ke，et al.Brazil split test of flattened disk and rock tensile strength using particle flow code[J].Journal of Central South University (Science and Technology)，2013，44(6):2499－2454.

[19]喻勇，徐跃良.采用平台巴西圆盘试样测试岩石抗拉强度的方法[J].岩石力学与工程学报，2006，25(7):1457－1462.YU Yong，XU Yue-liang.Method to determine tensile of rock using flattened Brazilian disk[J].Chinese Journal of Rock Mechanics and Engineering，2006，25(7):1457－1462.

[20]徐芝纶.弹性力学(第四版)[M].北京:高等教育出版社，2006:54－85.

[21]VAN CAUWELAERT F，ECKMANN B.Indirect tensile test applied to anisotropic materials[J].Materials and Structures，1994，27(1):54－60.

[22]JIANHONG Y，WU F，SUN J.Estimation of the tensile elastic modulus using Brazilian disc by applying diametrically opposed concentrated loads[J].International Journal of Rock Mechanics and Mining Sciences，2009，46(3):568－576.

[23]刘继国，曾亚武.岩石试件端面摩擦效应数值模拟研究[J].工程地质学报，2005，13(2):247－251.LIU Ji-guo，ZENG Ya-wu.Numerical simulation of the end frictional effect of rock specimens[J].Journal of Engineering Geology，2005，13(2):247－251.

[24]GRIFFITH A.The phenomena of rupture and flow in solids[J].Philosophical Transactions of the Royal Society of London:Series A，Containing Papers of a Mathematical or Physical Character，1921，221:163－198.