ITERATIVE REGULARIZATION METHODS FOR NONLINEAR ILL-POSED OPERATOR EQUATIONS WITH M-ACCRETIVE MAPPINGS IN BANACH SPACES∗

Department of Mathematical Sciences,Cameron University,Lawton,OK 73505,USA

E-mail:iargyros@cameron.edu

Santhosh GEORGE

Department of Mathematical and Computational Sciences,National Institute of Technology Karnataka,Surathkal-575025,India

E-mail:sgeorge@nitk.ac.in

ITERATIVE REGULARIZATION METHODS FOR NONLINEAR ILL-POSED OPERATOR EQUATIONS WITH M-ACCRETIVE MAPPINGS IN BANACH SPACES∗

Ioannis K.ARGYROS

Department of Mathematical Sciences,Cameron University,Lawton,OK 73505,USA

E-mail:iargyros@cameron.edu

Santhosh GEORGE

Department of Mathematical and Computational Sciences,National Institute of Technology Karnataka,Surathkal-575025,India

E-mail:sgeorge@nitk.ac.in

In this paper,a modifed Newton type iterative method is considered for approximately solving ill-posed nonlinear operator equations involving m-accretive mappings in Banach space.Convergence rate of the method is obtained based on an a priori choice of the regularization parameter.Our analysis is not based on the sequential continuity of the normalized duality mapping.

nonlinear ill-posed equations;iterative regularization;m-accretive operator; Newton type method

2010 MR Subject Classifcation47J05;47H09;49J30

1 Introduction

In this paper we are interested in approximately solving the ill-posed operator equation

where F:X→X is an m-accretive,Fr´echet diferentiable and single valued nonlinear mapping. Here and below X is a real Banach space with its dual space X∗.The norm of X and X∗are denoted by‖.‖and we write〈x,f〉instead of f(x)for f∈X∗and x∈X.The Fr´echet derivative of F at x∈Xis denoted by F′(x).

Recall that F is said to be m-accretive,if〈A(x1)-A(x2),J(x1-x2)〉≥0 for all x1,x2∈X, where J is the dual mapping on X and R(A+αI)=X for all α＞0,where I is the identity operator on X(see[2,Defnition 1.15.19]).

Throughout this paper we assume that X is strictly convex and has a uniform Gˆateaux diferentiable norm.The space X is said to be strictly convex if and only if for u,w∈S1(0):={x∈X:‖x‖=1}with u/=w,we have

and X is said to have a Gˆateaux diferentiable norm if

exists for each u,w∈S1(0).The space X is said to have a uniform Gˆateaux diferentiable norm if the above limit is attained uniformly for x∈S1(0).Equation(1.1)is,in general,ill-posed,in the sense that a unique solution that depends continuously on the data does not exist.Ill-posed operator equations of the form(1.1)in Hilbert spaces are studied extensively(see[12-17]and references there in).

It is known that[2,6,7,11,18],for accretive mapping F,the equation

There exists an element v∈X such that

where τ is some positive constant and Q is the normalized duality mapping of X∗.

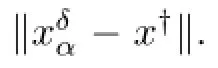
The organization of this paper is as follows.The method and its convergence is given in Section 2 and the error bounds under the source condition is given in Section 3.The paper ends with a conclusion in Section 4.

2 Method and Its Convergence

We will be using the following lemma from[18]for our analysis.

Lemma 2.1Let F:X→X be accretive and Fr´echet diferentiable on X.Then for any real α＞0 and x∈X,F′(x)+αI is invertible,

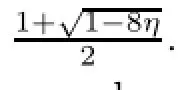
For constants a,d1,d with d1＞4,d＜a,let

The method(2.2)is a modifed simple form of the method considered in[11]and our analysis and conditions required for convergence are simpler than that in[11].

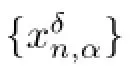
for all n＞1 where q:=k0η＜1.with k0is as in(2.1).

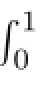
and

Again by Assumption 2.2 and Lemma 2.1 we have in turn

So by(2.4),(2.5),(2.6)and(2.7)we have

and hence by Lemma 2.1,Assumption 2.2 we have

so by Lemma 2.1,Assumption 2.2

Again since

3 Error Bounds Under Source Condition

In this section,we assume that x0-x†satisfes the source condition(1.7).The main result of this section is the following.

Theorem 3.1Let Assumption 2.2 and(1.7)hold.If 3k0r0＜1,then

where v is as in(1.7).

ProofWe have

and hence

Thus by(1.7),we have

Therefore by Lemma 2.1 and Assumption 2.2,we have in turn

This completes the proof of the Theorem.

By triangle inequality,(1.3),Theorem 2.3 and Theorem 3.1 we have the following.

Theorem 3.2Let the assumptions in Theorem 2.3 and 3.1 hold.Then

In the literature[7]the following stronger assumption is used.

Assumption 3.4(see[7,Theorem 2.3])There exists a constant¯k≥0 such that for every x,v∈B(ˆx,¯r)there exists an element k(x,ˆx,v)∈X such that

Notice that Assumption 3.4 implies Assumption 2.2 but not necessarily vice versa.Notice that

4 Conclusion

In this paper we considered a modifed Newton-type iterative method for approximately solving ill-posed equations involving m-accretive mappings in a real refexive Banach space with uniform Gˆateaux diferentiable norm.We obtained an optimal order error estimate based on an a priori choice of the parameter choice.

[1]Alber Ya I.On solution by the method of regularization for operator equation of the frst kind involving accretive mappings in Banach spaces.Diferential Equations SSSR,1975,9:2242-2248

[2]Alber Ya I,Ryazantseva I P.Nonlinear Ill-posed Problems of Monotone Type.Dordrecht:Springer,2006

[3]Argyros I K.Computational Theory of Iterative Methods.New York:Elsevier Publ Co,2007

[4]Argyros I K,Yeol Je Cho,George S.Expanding the applicability of lavrentiev regularization methods for ill-posed problems.Boundary Value Problems,2013,2013:114

[5]Buong Ng.Projection-regularization method and ill-posedness for equations involving accretive operators. Vietnamese Math J,1992,20:33-39

[6]Buong Ng.Convergence rates in regularization under arbitrarily perturbative operators.Annali di Mathematica,2003,43(3):323-327

[7]Buong Ng.Convergence rates in regularization for nonlinear ill-posed equations involving m-accretive mappings in Banach spaces.Appl Math Sci,2012,6(63):3109-3117

[8]Buong Ng.Convergence rates in regularization for nonlinear ill-posed equations under m-accretive perturbations.Zh Vychisl Matematiki i Matem Fiziki,2004,44:397-402

[9]Buong Ng.Generalized discrepancy principle and ill-posed equations involving accretive operators.J Nonl Funct Anal Appl,2004,9:73-78

[10]Buong Ng.On nonlinear ill-posed accretive equations.Southest Asian Bull Math,2004,28:1-6

[11]Buong Ng,Hung V Q.Newton-Kantorovich iterative regularization for nonlinear ill-posed equations involving accretive operators.Ukrainian Math Zh,2005,57:23-30

[12]Engl H W,Hanke M,Neubauer A.Tikhonov regularization of nonlinear diferential equations//Sabatier P C,ed.Inverse Methods in Action.New York:Springer-Verlag,1990:92-105

[13]Engl H W,Hanke M,Neubauer A.Regularization of Inverse Problems.Dordrecht:Kluwer,1993

[14]George S,Nair M T.A modifed Newton-Lavrentiev regularization for nonlinear ill-posed Hammerstein-type operator equations.J Compl,2008,24:228-240

[15]Semenova E V.Lavrentiev regularization and balancing principle for solving ill-posed problems with monotone operators.Comput Methods Appl Math,2010,4:444-454

[16]Tautenhahn U.On the method of Lavrentiev regularization for nonlinear ill-posed problems.Inverse Problems,2002,18:191-207

[17]Vasin V,George S.An analysis of lavrentiev regularization method and newton type process for nonlinear ill-Posed problems.Appl Math Comput,2014,2301:406-413

[18]Wang Ji’an,Li Jing,Liu Zhenhai.Regularization methods for nonlinear ill-posed problems with accretive operators.Acta Math Sci,2008,28B(1):141-150

[19]Liu Zhenhai.Browder-tikhonov regularization of non-coercive ill-posed hemivariational inequalities.Inverse Problems,2005,21:13-20

∗Received August 29,2014;revised May 11,2015.