CONSENSUS ANALYSIS AND DESIGN OF LINEARINTERCONNECTED MULTI-AGENT SYSTEMS∗

angzhou CHEN(陈阳舟)

College of Metropolitan TransportationBeijing Laboratory For Urban Mass Transit, Beijing University of Technology,Beijing 100124,China

E-mail:yzchen@bjut.edu.cn

Wei LI(李伟)

College of Metropolitan TransportationBeijing University of Technology,Beijing 100124,China Department of Electromechanical Engineering,Shijiazhuang Institute of Railway Technology, Shijiazhuang 050041,China

E-mail:mufuli@emails.bjut.edu.cn

Guiping DAI(代桂平)

College of Metropolitan TransportationBeijing University of Technology,Beijing 100124,China

E-mail:daigping@bjut.edu.cn

A.Yu.ALEKSANDROV

Faculty of Applied Mathematics and Control Processes,St.Petersburg State University, St.Petersburg,Russia

E-mail:alex43102006@yandex.ru

CONSENSUS ANALYSIS AND DESIGN OF LINEAR
INTERCONNECTED MULTI-AGENT SYSTEMS∗

Y

angzhou CHEN(陈阳舟)

College of Metropolitan TransportationBeijing Laboratory For Urban Mass Transit, Beijing University of Technology,Beijing 100124,China

E-mail:yzchen@bjut.edu.cn

Wei LI(李伟)

College of Metropolitan TransportationBeijing University of Technology,Beijing 100124,China Department of Electromechanical Engineering,Shijiazhuang Institute of Railway Technology, Shijiazhuang 050041,China

E-mail:mufuli@emails.bjut.edu.cn

Guiping DAI(代桂平)

College of Metropolitan TransportationBeijing University of Technology,Beijing 100124,China

E-mail:daigping@bjut.edu.cn

A.Yu.ALEKSANDROV

Faculty of Applied Mathematics and Control Processes,St.Petersburg State University, St.Petersburg,Russia

E-mail:alex43102006@yandex.ru

We deal with the state consensus problem of a general Linear Interconnected Multi-Agent System(LIMAS)under a time-invariant and directed communication topology. Firstly,we propose a linear consensus protocol in a general form,which consists of state feedback of the agent itself and feedback form of the relative states between the agent and its neighbors.Secondly,a state-linear-transformation is applied to equivalently transform the state consensus problem into a partial stability problem.Based on the partial stability theory, we derive a sufcient and necessary criterion of consensus convergence,which is expressed via the Hurwitz stability of a real matrix constructed from the parameters of the agent models and the protocols,and present an analytical formula of the consensus function.Lastly,we propose a design procedure of the gain matrices in the protocol by solving a bilinear matrix inequality.

linear interconnected multi-agent system(LIMAS);partial stability;statelinear-transformation;criterion of consensus convergence;consensus design

2010 MR Subject Classifcation34D06;93C05;90B18

1 Introduction

Interconnected multi-agent systems are a kind of multi-agent systems with inherent interconnections between the agents.They have a wide range of applications in various practical felds,for example,large arrays of micro electromechanical sensors and actuators[1],distributed power networks[2],biological networks[3],water distribution networks[4]and transportation networks[5]etc.Lots of studies have been devoted to the stability problem of the interconnected multi-agent systems[6,7],while equally important consensus or synchronization problem receives less attention.Consensus means that a group of agents reach agreement on a common value asymptotically or in a fnite time by negotiating with their neighbors.Existing studies on the consensus problem mainly focus on the multi-agent systems without the inherent interconnections among agents[8]-[11].In this paper,we consider the consensus problem of Linear Interconnected Multi-Agent Systems(LIMASs).Next we frst give an overview on the consensus or synchronization of interconnected multi-agent systems.

Motivated by cellular networks,Scardovi et al[12]studied a synchronization problem of nonlinear interconnected networks and provided a sufcient synchronization criterion,where the identical network components are made of species represented as input-output operators. Liu et al[13]continued the study of the synchronization problem and also derived a sufcient synchronization criterion by introducing the concept of incremental-dissipativity.Franci [14]further extended the work in[12]by tolerating some heterogeneity among the operators. Fradkov et al[15]considered a leader-follower output feedback synchronization problem for a network of nonlinear interconnected dynamical systems and also established a sufcient criterion of synchronization.Although the above works dealt with nonlinear models,the passivity property was required and only sufcient synchronization criteria were provided.

For LIMASs,motivated by interconnected power grid,Lee et al[16,17]dealt with the consensus problem and derived a sufcient consensus criterion.They required that the system also satisfes the passivity property and the communication topology is connected and balanced. Under the same assumptions,Russo[18]derived a sufcient consensus criterion of linear and nonlinear interconnected multi-agent systems via contraction theory.Furtat et al[19]considered a robust consensus problem of LIMASs with a leader and provided a sufcient consensus criterion under some strong assumptions.Cheng et al[20]considered a leader-follower consensus problem with undirected topology and linear interconnection subject to integral quadratic constraints and obtained a sufcient consensus criterion.

As seen above,even for LIMASs,only sufcient consensus criteria were obtained under some strong assumptions,for example,the passivity property and special communication topology. So,in this paper,we focus attention upon the study of the state consensus problem of general LIMASs under the assumption of general directed communication topology.The other complex cases will be dealt with in the future,such as the output consensus,the consensus of nonlinear systems or uncertain systems,and etc.

Compared with existing literature on LIMASs,the contributions of this paper consist of the following three aspects.The frst contribution is that we design a linear consensus protocol in a general form consisting of two parts.One is a state feedback of the agent itself,and the other is a cooperative protocol with generalized gain matrices,which is in the feedback form of therelative states between the agent and its neighbors.This consensus protocol possesses several advantages.The frst term can be used to change the dynamics of the agents independently. The second term with generalized gain matrices makes one able to choose diferent gain for each of the components in the relative states independently.The second main contribution is that we derive a sufcient and necessary condition for the LIMAS achieving consensus and give an analytical formula of the consensus function.The results are obtained by using a state-lineartransformation to equivalently transform the consensus problem into a stability problem with respect to partial variables(partial stability for short)of an auxiliary system.The state-lineartransformation has been proved to be an efcient tool in our previous study[21,22].Compared with those in[16,17],our obtained results at least have two improvements:

1)the requirements of the passivity property is discarded and the connected and balanced topology is generalized to any directed topology;

2)a sufcient and necessary consensus criterion is presented.

The third contribution is that we propose a design procedure of the gain matrices in the protocol by solving a bilinear matrix inequality.

The rest of the paper is organized as follows.In Section 2,we describe the consensus problem of LIMASs and apply a state-linear-transformation to set up a bridge between the consensus problem and a partial stability problem.The main results are derived in Section 3. In Section 4,we present a design procedure of the gain matrices via solving a bilinear matrix inequality.In Section 5,some simulation examples are presented to verify our results.Finally, the conclusion is stated in Section 6.

2 Problem Description and its Relation to Partial Stability

We consider a LIMAS consisting of N heterogenous agents

The control input uiwill be designed based on available information.We assume that at any time t the agent i can measure its own state xi(t)and receive the relative state xj(t)-xi(t) between it and its communication neighbor j.The agent j is said to be a communication neighbor of the agent i,if the agent i can receive the information from the agent j via communication.We use Nito denote the index set of all the communication neighbors of the agent i and call the set N={Ni:i=1,···,N}a communication topology of the LIMAS(2.1).As seen in literature,the communication topology can also be described by a digraph.

Arbitrarily given a time-invariant communication topology N={Ni:i=1,···,N},we construct a consensus protocol of the following structure:

where Ki,Wij∈Rm×nare the gain matrices required to design of-line.The frst term in(2.2) with the gain matrix Kiis a state feedback of the agent i itself and is applied to independently regulate its own behavior.In fact,later one will see that it may change the fnal consensus dynamics of the agents.The second term with the matrices Wijare relative state feedbacks between the agent i and its neighbors and are applied to cooperate the agents for achieving consensus.The matrix Wijis well-defned for the indices i,j satisfying j∈Niand Wij=0 for any other indices i,j∈{1,···,N},i/=j.

where the superscript T denotes the transpose of a matrix or vector,and the matrices in(2.3) are defned as follows:

A={Aij,i=1,···,N,j∈Ωi}is a block matrix with matrix blocks Aijat(i,j)for j∈Ωiand 0 matrices at other places,

B=diag{B1,···,BN}is a diagonal block matrix with diagonal matrix blocks Bi,

K=diag{K1,···,KN}is a diagonal block matrix with diagonal matrix blocks Ki,

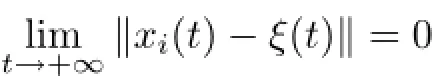
For the communication topology N={Ni:i=1,···,N}and the protocol(2.2),we are concerned about three issues:1)to fnd a criterion of consensus convergence,2)to calculate the consensus function of the agents if the LIMAS(2.1)achieves global consensus,and 3)to propose a design procedure of the gain matrices in the protocol(2.2).

Now we apply a state linear transformation proposed in[21,22]to the system(2.3)and equivalently transform the consensus problem of the LIMAS(2.1)into an asymptotically partial stability problem of a corresponding system.The state linear transformation is as follows:

where1N∈Rnrepresents a column vector with 1 as its components,Instands for an identity matrix of dimension n,ei,i=1,···,N,are the standard row vectors with 1 in the ith column and 0 in the other columns,and⊗denotes the Kronecker product of matrices or vectors.

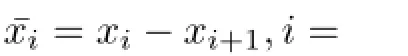
where the inverse matrix of the matrix P can be exactly calculated as follows:

The matrices in(2.8)are represented as follows

Before building a bridge between the consensus problem of the LIMAS(2.1)under the protocol(2.2)and the partial stability problem of the system(2.8),we give the following defnition.

Now we prove a key lemma to express the relation of the consensus problem to the asymptotic y-stability problem.

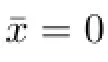
3 Convergence Criterion and Consensus Function

According to the result in[23],we have that the asymptotic y-stability of(2.6)or(2.8)is equivalent to asymptotic stability of the following auxiliary linear system:

where ζ=[yTηT]Tand η is an extended state.The matrices L1and L3are derived from the matrix

through the following steps:

Step 1Calculate the minimal integer s such that rankVs=rankVs+1,where Vsand Vs+1are of the form in(3.2);

Step 2Let h=:rankVsand construct h×n matrix L1,the rows of which are linearly independent rows of matrix Vs;

Step 3Construct h×h matrix L2,which is consisted of the linearly independent columns in L1,say,the columns i1,···,ihin L1;

The following lemma shows the relation between y-stability of the system(2.8)and the stability of the auxiliary system(3.1).

Lemma 3.1(see[23])The equilibrium point¯x=0 of the system(2.8)is asymptotically y-stable if and only if the equilibrium point ζ=0 of the corresponding auxiliary system(3.1) is asymptotically stable.

Now we state and prove our main results as follows.

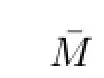
ProofBy Lemma 2.3 and Lemma 3.1,the sufcient and necessary condition can be directly verifed.So we focus the calculation of the consensus function.First,by Lemma 2.3 the consensus function(3.3)can be obtained from ξ(t)=N-1z(t),where z(t)is calculated from the second equation in(2.8)as follows

From the construction of the auxiliary system(3.1)we know that y(t)is the frst(N-1)n elements of the state ζ(t)in(3.1),and thus we have

where ζ(t)can be calculated from the system(3.1)as follows:

Finally,noticing the identities

we get the consensus function(3.3)by substituting the relations(3.4)-(3.8)into the expression ξ(t)=N-1z(t).The proof is completed.?

Remark 3.3The authors in[16,17]gave a sufcient condition under the strong assumption of connected and balanced communication topology,which is expressed by the passivity of the LIMAS.However,our results show that the LIMAS can achieve global state consensus even if the passivity condition in[16,17]is not held(see Example 2 in the section 5).Thus,we have improved the result in[16,17]in two aspects:1)the limit on the communication topology is removed,and 2)a sufcient and necessary criterion is derived.

Theorem 3.2 includes the following two extreme cases.

Corollary 3.4The following statements are correct:

1)If rankVn=0,the necessary and sufcient condition for LIMAS(2.1)achieving state consensus is that the matrix¯A in(2.9)is Hurwitz stable.

2)If rankVn=n,the necessary and sufcient condition for the LIMAS(2.1)achieving state consensus is the matrix M in(2.3)is Hurwitz stable.

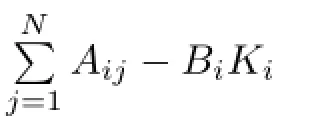
4 Consensus Protocol Design

In this section,we consider the design problem of the consensus protocol(2.2).

It is well known that the Hurwitz stability of the matrix¯M in Theorem 3.2 is equivalent to that there exits a positive matrix Q satisfying the following Lyapunov inequality:

We assume that the gain matrix Kiin the protocol(2.2)has been designed in advance since its role is to change the fnal consensus dynamics of the agents.Thus,(4.1)can be written as:

where henceforth the asterisk(∗)denotes the previous item and

Δij=[δmn]N×Nis a matrix with entries

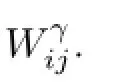
Step 2solve the optimization problem with LMI constrains

where∈1is a positive small number.

where τ1,τ2is the perturbation range.

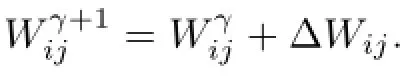
Step 5if|t(γ+1)-t(γ)|＜∈2for a positive small real number∈2＞0,which means that the calculation of the gain matrices Wijcan not be improved any further,or the iteration counter reaches the maximum number of iteration,the iteration terminates.

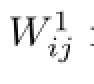
5 Simulation Examples

In this section,we consider several numeral examples to explain our results.

Example 1Consensus analysis of a second-order LIMAS consisting of 3 agents.

We consider the example in[16]of a second-order LIMAS(2.1)consisting of 3 agents with the following parameter matrices Aii,Aijand Bi:

and a time-invariant communication topology N1={2,3},N2={1,3},N3={1,2}.We test the consensus for the following gain matrices in protocol(2.2):

One can verify that rankV2=2,which is the case 2 in Corollary 1.In this case,we show that M is Hurwitz stable by calculating its eigenvalues-5.2498±1.4951i,-1.2412±0.4075i,-5.0181, -3.0000.Thus LIMAS(2.1)achieves global state consensus and all the agents convergence to the zero states.Fig.1(a)(b)show the state trajectories of the agents starting from the initial states[5,2]T,[2,1]T,[-3,-2]T,respectively.

Example 2Consensus Design of a third-order LIMAS consisting of 4 agents.

Now we consider the design problem of a third-order LIMAS(2.1)consisting of 4 agents with the following parameter matrices Aii,Aijand Bi:

and a time-invariant imbalanced communication topology N1={2},N2={3,4},N3={1}, N4={2}.We frst take the gain matrices Ki,i=1,2,3,4,in protocol(2.2)as

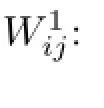
One can verify that rankV2=2,and the matrix¯M in(3.1)is Hurwitz stable by calculating its eigenvalues-5.9302,-19.6374±5.0463i,-5.896144±3.4774i,-1.7182,-0.0055±3.6995i, -0.0779±0.3331i.Thus,LIMAS(2.1)achieves global states consensus.However,the passivity condition ATQ+QA＜0,QB=CTrequired in[17]is not satisfed since the matrix A is not Hurwitz stable,where A and B are the matrices defned in(2.3),C=I12in this example.Fig.2 (a)(b)(c)show the state trajectories of the agents starting from the initial states[4.2,5.4,25]T, [6.3,3.5,40]T,[3.4,4.6,50]T,[4.5,6.9,29]T,respectively.

6 Conclusions

In this paper,the state consensus problem of LIMASs with time-invariant and directed communication topology is considered by applying a state-linear-transformation approach.A sufcient and necessary criterion of consensus convergence in terms of matrix stability is proposed and an analytical expression of the consensus function is given.A design procedure of the consensus protocol is also presented by solving a bilinear matrix inequality.

Although we only studied the state consensus of LIMASs with time-invariant communication topology and in absence of communication time-delay,the approach in this paper can be applied to more complex consensus problems,for example,the cases with time-varying communication topology or/and communication time-delays,the output or part-state consensus,and etc.,which will be considered in the future.

[1]Napoli M,Bamieh B.Modeling and observer design for an array of electrostatically actuated microcantilevers.Proceedings of the 40th IEEE Conference on Decision and Control,2001:4274-4279

[2]Venkat A N,Hiskens I A,Rawlings J B,et al.Distributed output feedback MPC for power system control. Proceedings of the 45th IEEE Conference on Decision and Control.2006:4038-4045

[3]Omony J,de GraafL H,van Straten G,et al.Modeling and analysis of the dynamic behavior of the XlnR regulon in Aspergillus niger.BMC systems biology,2011,5(Suppl 1):S14

[4]Bragalli C,D’Ambrosio C,Lee J,et al.Case Studies in Operations Research.New York:Springer,2015, 212:183-198

[5]Han X G,Chen Y Z,Shi J J,et al.An extended cell transmission model based on digraph for urban trafc road network.Proceedings of the 15th IEEE Conference on Intelligent Transportation Systems, 2012:558-563

[6]Yang T C.Networked control system:a brief survey.IEE Proceedings-Control Theory and Applications, 2006,153(4):403-412

[7]Heemels W,van de Wouw N.Networked Control Systems.London:Springer,2010:203-253

[8]Shang Y.Consensus formation of two-level opinion dynamics.Acta Mathematica Scientia,2014,34B(4): 1029-1040

[9]Guo W,Xiao H,Chen S.Consensus of the second-order multi-agent systems with an active leader and coupling time delay.Acta Mathematica Scientia,2014,34B(2):453-465

[10]Olfati-Saber R,Fax J A,Murray R M.Consensus and cooperation in networked multi-agent systems. Proceedings of the IEEE,2007,95(1):215-233

[11]Ren W,Cao Y.Distributed Coordination of Multi-agent Networks:Emergent Problems,Models,and Issues.London:Springer,2010

[12]Scardovi L,Arcak M,Sontag E D.Synchronization of interconnected systems with applications to biochemical networks:An input-output approach.IEEE Transactions on Automatic Control,2010,55(6): 1367-1379

[13]Liu T,Hill D J,Zhao J.Incremental-dissipativity-based synchronization of interconnected systems.Proceedings of the 18th IFAC World Congress,2011:8890-8895

[14]Franci A,Scardovi L,Chaillet A.An Input-Output approach to the robust synchronization of dynamical systems with an application to the Hindmarsh-Rose neuronal model.Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference,2011:6504-6509

[15]Fradkov A,Junussov I,Ortega R.Decentralized adaptive synchronization in nonlinear dynamical networks with nonidentical nodes.Proceedings of the 2009 IEEE International Symposium on Control Applications and Intelligent Control,2009:531-536

[16]Lee S J,Oh K K,Ahn H S.Passivity-based output synchronisation of port-controlled Hamiltonian and general linear interconnected systems.IET Control Theory and Applications,2013,7(2):234-245

[17]Lee S J,Ahn H.Passivity-based output synchronization of interconnected linear systems.Proceedings of the IEEE/ASME International Conference on Mechatronics and Embedded Systems and Applications,2012: 46-51

[18]Russo G.Analysis,Control and synchronization of nonlinear systems and networks via Contraction Theory: theory and applications.Universita degli studi di Napoli Federico II,2010

[19]Furtat I,Fradkov A,Tsykunov A.Robust synchronization of linear dynamical networks with compensation of disturbances.International Journal of Robust and Nonlinear Control,2014,24(17):2774-2784

[20]Cheng Y,Ugrinovskii V A.Guaranteed performance leader-follower control for multi-agent systems with linear IQC coupling.Proceedings of the 2013 IEEE conference on American Control Conference,2013: 2625-2630

[21]Ge Y R,Chen Y Z,Zhang Y X,et al.State consensus analysis and design for high-order discrete-time linear multiagent systems.Mathematical Problems in Engineering,2013:Art ID192351

[22]Chen Y Z,Ge Y R,Zhang Y X.Partial stability approach to consensus problem of linear multi-agent systems.Acta Automatica Sinica,2014,40(11):2573-2584

[23]Vorotnikov V I.Partial Stability and Control.Boston:Springer,1998

[24]Wang Y G.BMI-based output feedback control design with sector pole assignment.Acta Automatica Sinica, 2008,34(9):1192-1195

[25]Fukuda M,Kojima M.Branch-and-cut algorithms for the bilinear matrix inequality eigenvalue problem. Comput Opt Appl,2001,19(1):79-105

[26]Shimomura T,Fujii T.Multiobjective control via successive over-bounding of quadratic terms.International Journal of Robust and Nonlinear Control,2005,15(8):363-381

∗Received January 12,2015;revised May 18,2015.This work was supported in part by NSF of China(61273006 and 6141101096),High Technology Research and Development Program of China(863 Program)(2011AA110301),Specialized Research Fund for the Doctoral Program of Higher Education of China(20111103110017),St.Petersburg State University(9.38.674.2013)and the Russian Foundation for Basic Research(13-01-00376-a and 15-58-53017).